. . . being based on so flimsy a foundation, a practical theory of the future . . . is subject to sudden and violent changes.
John Maynard Keynes (1937)
False pretences of knowledge about complicated economic situations have become all too common in public policy debates. While we do know some things, we don’t know everything. We believe that prudent decision-making should acknowledge what we don’t know. Decision makers should strive to quantify dimensions of their ignorance and adjust their decisions accordingly. This essay describes a tractable approach for acknowledging, characterizing, and responding to the limited understandings discovered by researchers’ efforts to interpret existing evidence by using theories and statistical methods available at any particular moment.
An economic model tells how chance, occurrences, and purposeful decisions influence future outcomes. Economic researchers use formal statistical models to describe and interpret data and to formulate policy advice for government and private decision makers. Whether they acknowledge it explicitly or not, real world decision makers also use models or ‘views’ about how their decisions affect future outcomes. Because they ignore some forces and oversimplify others, all models are just approximations to reality, some better than others depending on the purposes to which they are put. Furthermore, at any time, we can choose among multiple models and are unsure how much credibility to assign to each of them.
Data can surely help us assess the credibility of alternative models, but the real world is so complicated and data are so limited that data can only tell us so much. Therefore, economic modellers and decision makers require ways to express their opinions about the plausibility and usefulness of alternative models for the problem at hand. Because data are only partially informative about a model’s plausibility, a decision-maker’s purpose as well as his or her ‘subjective beliefs’ play important roles too. The more complex the situation, the bigger the challenge of confronting uncertainty.
Economists and other scholars have created theoretical foundations for uncertainty. For instance, both John Maynard Keynes (1921) and Frank Knight (1921) wrote on the subject, but mostly in literary ways that are challenging to interpret and to make operational so that they can be applied in quantitative work. The eminent statistician Abraham Wald (1950) introduced a theoretic framework for making decisions under uncertainty. Leonard J. Savage (1954) constructed a complete axiomatic approach to Bayesian decision theory by including subjective probabilities that are entirely in the mind of a decision maker. Itzhak Gilboa and David Schmeidler (1989) extended this approach in ways that acknowledged that a decision maker might not have a unique subjective probability distribution. Recent research in control theory and in dynamic decision theory provides useful practical tools for assessing and coping with various sources of uncertainty. We have worked on these topics for a number of years. Along with others, we have used mathematics and statistics to construct operational quantitative tools that shed light on how financial markets and the macroeconomy work and how alternative fiscal and monetary policies affect them.
In a recent paper (Hansen and Sargent 2019), we propose ways to categorise and respond to the multiple forms of uncertainty that confront decision makers and model builders. Thus, we distinguish among (1) uncertainty within a model; (2) uncertainty across a set of available known models; and (3) uncertainty about each model. We refer to (1) as risk – uncertainty about future outcomes that is described by a single known probability distribution. (This is the type of uncertainty assumed up until now in most work in theoretical and applied finance and macroeconomics.) We call uncertainty of type (2) ambiguity and represent it as being unsure about what weights or probabilities to attach to the available models. We call (3) model misspecification and represent it by surrounding each available model with a vast cloud statistical models with unknown forms that nevertheless fit the available data nearly as well as does an available model.
The models that we economists build and use are highly stylised. We design them partly to analyse how random impulses that we call shocks have effects that are transmitted across time. Shocks that vitally interest macroeconomists include unanticipated improvements in technologies and unanticipated changes in monetary policy actions. We interpret the fact that distinguished macroeconomists and economic historians disagree about prospects for long-term economic growth and for the efficacy of monetary policy as indicating the economic profession’s ambiguity about and lack of confidence in available models.
Our paper is part of a broader research agenda we are pursuing to develop and apply convenient practical tools for measuring how uncertainty, scepticism, and confidence affect prices and quantities in financial markets. Thus, imagine investors who are unsure about long-term prospects for ‘secular stagnation’1 in macroeconomic growth because they don’t know about prospective movements in demographics, technologies, and global trade restrictions. These investors have multiple models (maybe they call them ‘views’), but they are not fully confident about any of them. Moreover, these investors suspect that the detailed structures of the models that express their ‘views’ do imperfect jobs of translating their imprecisely formulated ‘views’ and ‘hunches’ into mathematical-statistical models. The flaws themselves are unknown and thus not immediately correctable. Such a perspective about model scepticism broadens the notion of uncertainty relative to the standard risk aversion paradigm (our type (1) uncertainty above) that today mostly dominates economic analysis and discourse. It also refines our understandings of the prices of uncertainty and how they fluctuate over time.
We offer a formal structure and a quantitative illustration that focuses on uncertainty about macroeconomic growth and its persistence. In our example, we confront investors with uncertainty about the future of macroeconomic growth. We do this in a stylised way that can capture both the worrisome secular stagnation feared by some macroeconomists and the uncertain prospects for technological advances debated by economic historians. In our quantitative illustration, we find that prices of uncertainty fluctuate because investors especially fear high persistence of macroeconomic growth in bad states, and fear low persistence in good ones. Why this asymmetry? When an economy is growing, the salient fear preoccupying investors is that high growth will not persist. But when the economy is stagnant, the salient fear is that sluggishness will persist. We show how these concerns manifest themselves in terms of both our type (2) (i.e. model ambiguity) and the type (3) uncertainty (i.e. model misspecification). We show how these manifestations take the form of an endogenous nonlinearity in the ‘discount factor’ that investors use to evaluate the prospective payout streams that underlie asset evaluations. This nonlinearity compounds itself over time in ways that provide a new explanation for how asset market fluctuations reflect uncertainty.
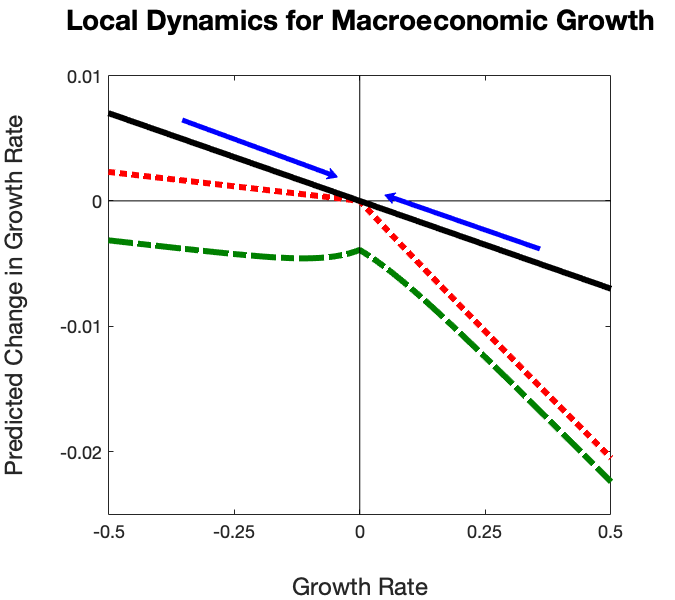
Figures 1 and 2 illustrate how we can depict key objects at play when investors make portfolio decisions while juggling our three types of model uncertainty about the multiple models that express their ‘views’ about the economy. Suppose that investors start with a simple linear first-order autoregressive model of macroeconomic growth rate dynamics but that their concerns about uncertainty induce them to explore other statistically similar specifications including ones that they especially fear. In Figure 1, the linear relation with the negative slope captures their baseline model with so-called mean reversion in growth rates. The mean reversion is evident because there is a pull from the more extreme growth states towards the centre of the growth rate distribution. The vertical axis is the local pull towards the centre of the distribution of macroeconomic growth (net of its long-run average growth rate.) If zero is the centre point, then in the absence of random shocks, there is a pull towards zero. The kinked line in red emerges when our investors consider formally many other possible and statistically similar specifications and when they then compute another model that investors fear might apply and that is statistically similar to the baseline linear model. The flatter slope to the left of zero reflects investors’ concerns in bad economic times that the macroeconomy may be stuck with more growth sluggishness than in the original model. The steeper slope to the right of zero reflects opposite forces. Here, good macroeconomic growth outcomes are feared to be shorter lived than in the original model specification. The blue and green curves show further adjustments induced by overall concerns that all of the models listed so far are wrong (misspecified). The overall downward shift occurs because the investors are averse to all of these different forms of uncertainty. While this presentation is informal, in our paper we develop these ideas, including the connections to statistical perspectives, in formal ways that are amenable to computation.
Figure 1 Local dynamics for macroeconomic growth
Notes: Black solid: baseline linear model; red: incorporates model ambiguity; green: incorporates concerns about model misspecification in addition to model ambiguity.
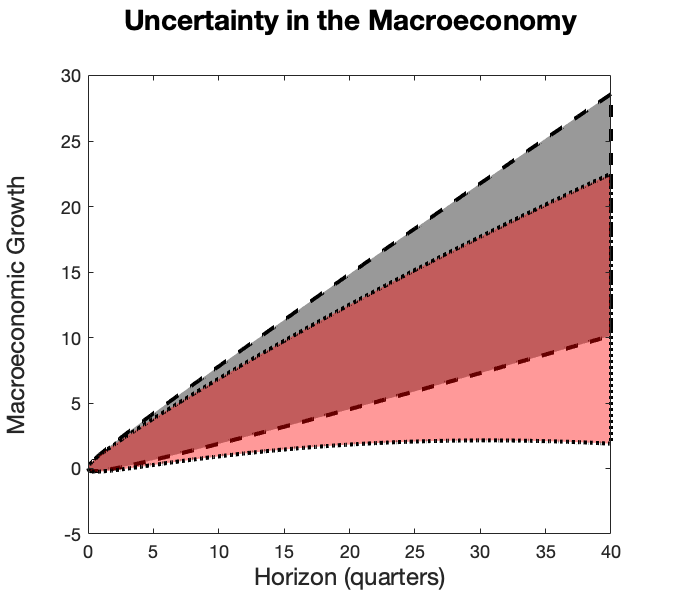
Figure 2 Distribution of macroeconomic growth rates over different horizons
Notes: The grey shaded area between the dashed lines depicts the interval between the .1 and .9 deciles for every choice of the horizon under the baseline model. The red shaded area between the dotted lines gives the region within the .1 and .9 deciles under the worst-case model and includes both model ambiguity and model misspecification concerns.
While Figure 1 targets the local dynamics, Figure 2 looks at how the implications are compounded over time by plotting deciles of implied macro consumption distributions over alternative horizons. For sake of simplicity, we depict only the results comparing the base line black line to the distributions associated with the green curve. The grey region depicts the baseline distribution, and the red region shows the impact of the uncertainty adjustment obtained by twisting probabilities in a conservative direction indicative of more cautious decision making in the face of uncertainty. This exercise holds fixed the constellation of their ‘views’. What varies, and what is being depicted in the figure, is the tractable way in which investors respond cautiously to the three types of uncertainty associated with their views.
We began this column by lamenting the false pretences of knowledge about complicated economic situations and overconfidence that are common in public policy debates. We close by responding to the commonly heard objection that recommends being cautious and taking into account that our three types of uncertainty are bound to lead to paralysis and to ‘do nothing’ policies. To the contrary, in a variety of interesting macroeconomic examples, acknowledging model ambiguity and misspecification leads to policies that are engineered to work well across a range of available ‘views’. Robustness of outcomes across a range of views is accomplished by crafting policies that are relatively insensitive to details in individual models. The resulting policies are cautious in the sense that they take into account potentially adverse outcomes that could occur under at least some of the ‘views’ that the decision maker wants to consider.
References
Gilboa, I and D Schmeidler (1989), “Maxmin Expected Utility with Non-unique Prior”, Journal of Mathematical Economics 18(2): 141-53.
Hansen, L P and T J Sargent (2019), “Macroeconomic Uncertainty Prices when Beliefs are Tenuous”, NBER Working Paper 25781.
Keynes, J M (1921), Treatise on Probability, Macmillan.
Keynes, J M (1937), “The General Theory of Employment”, The Quarterly Journal of Economics 51(2): 209-223.
Knight, F H (1921), Risk, Uncertainty and Profit, Houghton Mifflin.
Savage, L J (1954), The Foundations of Statistics, Wiley.
Wald, A (1950), Statistical Decision Functions, Wiley.
Endnotes
[1] A concept from the late 1930s, “secular stagnation” refers to the condition that asserts that growth rates will be disappointing and sluggish long into the future.