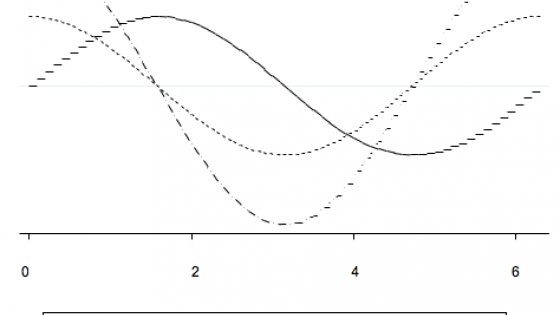
Does the Eurozone constitute an optimum currency area? Most of the literature on this issue has focused on co-movements in the cycle as a measure of synchronisation.1 But this can be misleading if the amplitudes of the cycle are very different, as illustrated in Figure 1, which shows two countries sharing the same (highly stylised) business cycle, but whose amplitudes are very different. This has two implications – the correlation coefficient between the two series is one, but large differences appear at the peak and trough of the cycle. These differences can lead to similar problems of common policymaking as if the two cycles are not correlated, as the high beta country B would need higher interest rates at the peak (and lower ones at the bottom) of the cycle than country A. The divergence created by different amplitudes thus appears mostly at the extremes of the cycle.
Figure 1. Perfect co-movement but different amplitudes
Notes: This figure shows stylised business cycles for countries A and B. The business cycles are synchronous, with country B having an amplitude that is twice as large as that of country A.
These considerations suggest that the emphasis on correlations makes sense only if countries have cycles that do not coincide, but have a similar amplitude (and length). Figure 2 depicts the case of two countries whose cycles are shifted over time in such a way that the correlation coefficient is equal to zero. In this case the differences in the cyclical positions remain constant for a long period between the peak of one cycle and the trough of the other, but then go to zero and change sign.
Figure 2. Zero correlation because of phase shift
Note: This figure shows stylised business cycles for countries A and C with the same amplitude but that are uncorrelated.
A comparison between these two figures suggests one way in which one could discriminate between the two hypotheses – if differences in amplitudes are the problem, one would expect large divergences to appear mainly at the peak and trough of the cycle. By contrast, if business cycles are shifted, the divergences in cyclical positions should persist most of the time. The way the policy discussion has evolved suggests that different amplitudes might have been a key factor since differences in cyclical positions play a smaller role today than they did at the peak of the crisis.
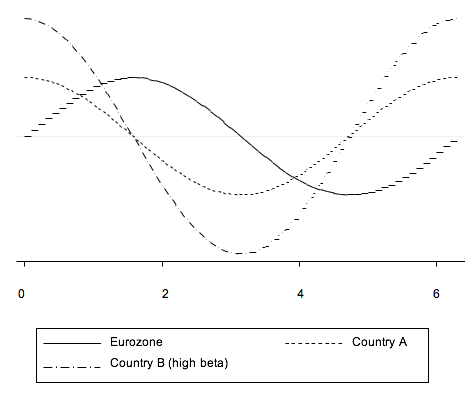
Moreover, differences in amplitude can magnify the impact of any de-synchronisation, as illustrated in Figure 3, which shows three lines: the common Eurozone cycle; the cycle of a country that is delayed by half a cycle, but has the same amplitude as the common cycle; and a country with an amplitude twice as large as the common cycle. It is apparent that the difference between the national and the Eurozone cycle is not the same when the amplitude changes, although the correlation coefficient between the national and the Eurozone cycle is equal (to zero) in both cases.
Figure 3. Correlation and phase shift
Note: This figure plots the business cycle of three economies: the euro area, country A, which is shifted, and country B, which is shifted and has an amplitude twice as large as that of country A.
Amplitudes: Stylised patterns for the Eurozone
A first measure of different amplitudes is the volatility of business cycles at the national level, proxied by the standard deviation of the cyclical component of national real output (GDP). A first question is thus whether there has been convergence in the amplitude of business cycles measured by their overall volatility (Gayer 2007). As many have before us, we rely on the HP filter for the trend-cycle decomposition.
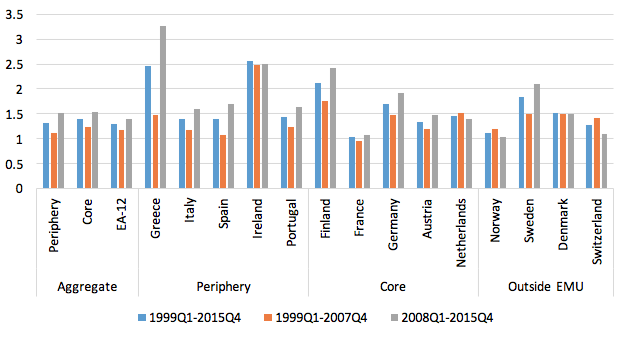
To measure the impact of the Eurozone crisis, we split the sample between the early phase of the euro (1999Q1-2007Q4) and the crisis period (2008Q1-2015Q4), but also provide the standard deviation for the whole period from 1999Q1 to 2015Q4. The results are depicted in Figure 4. We group the countries into core (those without financial distress 2011/12), periphery, and also consider non-Eurozone countries.
Figure 4. Amplitude of business cycles
Notes: Standard deviations of output gap in %.
Source: Authors’ own computations based on Commission AMECO data.
The overall picture that emerges from Figure 4 is that there are large differences in the amplitudes of business cycles across countries, but that these differences do not reflect a core-periphery dimension (the group averages shown in the first columns are very similar). The ‘Great Moderation’ is apparent if one considers the first period after the introduction of the euro. By comparing the second and third bars, one sees that amplitudes of the business cycle clearly increased with the crisis, but the increase is proportionally contained (usually around 20 to 30% of the pre-crisis value).
Greece of course is an outlier, but for another crisis-hit country – Ireland – one sees no change in the amplitude of the cycle. Among the core countries, Finland, the Netherlands, and, surprisingly, Germany stand out, whereas France shows the lowest variation.
Beta: Stylised patterns for the Eurozone
For the functioning of the Eurozone, the more relevant question is whether national cycles of individual countries had a different reactivity to the aggregate EZ12 cycle — that is, whether different countries had different ‘betas’. To measure these ‘betas’, we ran some simple regressions in which we explained the national cyclical component of growth only by the common Eurozone cycle.2
The results are shown in Figures 5 and 6.3
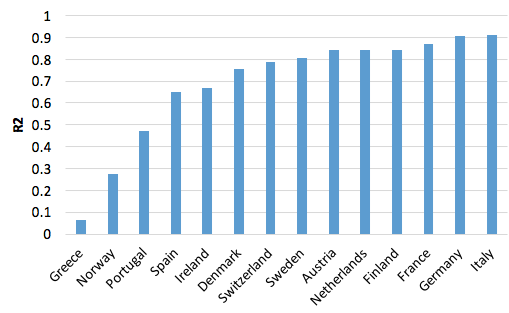
Figure 5. How important is the common cycle for the national cycle: R2
Notes: R2 correspond to the same regression equation explained in footnote 3 and the betas in Figure 6.
Figure 5 shows that most national cycles are tightly linked to the Eurozone’s cycle as the R2 — that is, the proportion of the variability of the national cycle that can be explained by the common Eurozone cycle, is generally greater than two-thirds. Greece is the one clear exception, in that the common cycle seems to be irrelevant for that country. Portugal displays a somewhat lower explanatory power of the common cycle, but it remains highly relevant. The countries belonging to the core show a somewhat tighter correlation, with R2 generally above 80%, with lower values among the peripheral countries.
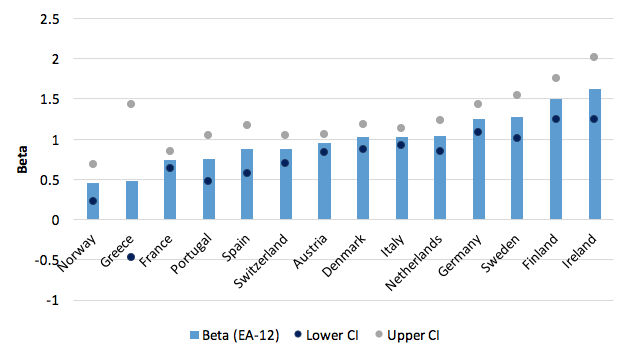
Figure 6. Contemporaneous effect of the EZ12 cycle on the national cycle: Betas
Notes: Dependent variable is the quarterly (HP filtered) cyclical component of each peripheral country. The sample runs from 1999Q1 - 2015Q4. The coefficients are statistically significant at the 1% level for all countries except for Greece whose coefficient is not significant at any conventional level. Upper and lower CI refer to the 95% confidence interval.
The beta coefficients are in general quite precisely estimated. In six out of the 14 countries, the estimated coefficient is more than two standard deviations from one. One could thus argue that for these countries the optimum currency area criterion is not fulfilled, despite the high correlations found above. Moreover, even within the core (generally considered a rather homogenous group) there is a large, statistically significant difference between Germany and France – Germany’s beta is almost twice as large as that of France (1.25 and 0.74, respectively). This means that if the common cycle shows an output gap of 2%, that of France (compared to its own cycle) would be 1.48%, whereas that of Germany would be 2.5%. Any large common upswing or downswing could thus lead to very large cyclical positions. The null hypothesis that the beta is equal to one can be rejected for three of the core countries. Within the periphery, one also finds pronounced differences, with Ireland having a beta of 1.63, compared to 0.87 for Spain. Italy is the only large country with a point estimate of its beta almost exactly equal to one.4
Somewhat surprisingly, we also find that the business cycles of most non-EMU European countries are as tightly linked to that of the Eurozone as are those of the average EMU member countries (see Belke et al. 2016). Except for Norway (which isn’t surprising given the importance of oil and gas), the R2 is between 0.75 and 0.80.
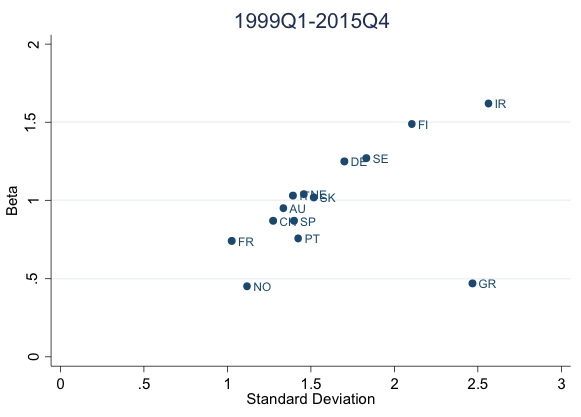
Figure 7. Beta versus standard deviation
Notes: The scatter plots show the standard deviation of the output gap from Figure 4 against the beta from regressions in Figure 6 (period 1999Q1 - 2015Q4). Belke et al (2016) provide similar data for the sub-periods 1999Q1-2007Q4 and 2008Q1-2015Q4.
The large differences in the elasticity with which different countries react to the common Eurozone cycle beg the question whether these differences can also explain the large differences in the amplitude of national cycles discussed earlier.
Figure 7 therefore shows a scatter diagram of the standard deviations in Figure 4 against the beta coefficients reported in Figure 6.
The amplitudes of the national business cycles are clearly tightly correlated with the beta, or the ‘elasticity’ with which the national cycle reacts to the common one. The exception is, again, Greece, whose economy seems to have followed a completely different path since the outbreak of the crisis. The close correlation between the estimated beta coefficients and the standard deviation of national cycles suggests that the much higher variability observed in some countries was not due to a divergent national cycle or specific policy errors, but to the structure of the economies and their financial sectors, which seem to make certain economies react much more strongly to the common cycle than others.
The analysis of the pre- and post-crisis sub-periods contained in Belke et al. (2016) shows that these patterns have not been fundamentally affected by the crisis, although one finds some general decrease in correlation between core and peripheral countries.
Conclusions
Business-cycle synchronisation is a key criterion for optimum currency areas. The standard argument is that membership in a common currency area becomes costly for any country whose national cycle diverges significantly from the common cycle.
We find that for most EMU member countries there is a tight correlation between the national cycle and the common cycle. At first sight it thus appears that, with the exception of Greece (and possibly Portugal), the standard optimum currency area criterion is fulfilled. But our key argument is that it is not sufficient to look at correlation patterns. Countries that share the same business cycle might nevertheless experience quite different cyclical positions, and thus require a different monetary policy stance if the amplitude of the cycle is very different. We indeed find large systematic differences in the amplitude of national cycles and the degree to which the national cycle reacts to the common one, with many countries registering a ‘beta’ that is significantly different from one.
The practical conclusion for the Eurozone is that the main problem for the ECB might not be a de-synchronisation of cycles, for example between the core and the periphery. Instead, a more relevant problem in practice might be that individual countries have cycles that are tightly correlated, but of very different amplitudes, thus requiring at times a different monetary policy stance at the peak than at the trough. The more general conclusion is that a high degree of correlation is not a sufficient optimum currency area criterion. Having a beta that is close to one is equally important.
References
Bayoumi, T and B Eichengreen (1993) “Shocking aspects of European monetary integration” in F Torres and F Giavazzi (eds), Adjustment and Growth in the European Monetary Union, Cambridge: Cambridge University Press.
Belke, A, C Domnick and D Gros (2016) “Business cycle synchronization in the EMU: Core vs periphery”, CEPS, Working Document No 427, Brussels.
Campos, N F and P Macchiarelli (2016) “Core and periphery in the European Monetary Union: Bayoumi and Eichengreen 25 years later”, Economics Letters, 147: 127–130.
De Grauwe, P and Y Ji (2016) “Flexibility versus stability: A difficult trade-off in the Eurozone”, CEPS, Working Document No 422, Brussels.
de Haan, J, R Inklaar and R Jong-A-Pin (2008) “Will business cycles in the Euro area converge? A critical survey of empirical research”, Journal of Economic Surveys, 22(2): 234–273.
Gayer, C (2007) “A fresh look at business cycle synchronisation in the euro area”, European Economy, Economic Paper No 287, October, Brussels.
Gogas, P (2013) “Business cycle synchronisation in the European Union”, Journal of Business Cycle Measurement and Analysis, (1):1-14.
Endnotes
[1] Bayoumi and Eichengreen (1993) is the canonical reference, with Campos and Macchiarelli (2016) providing a timely update. See De Haan et al. (2008) for a recent survey of the literature.
[2] See Belke et al. (2016) for further details.
[3] As a robustness check, we exclude for all regressions the reference country i from the EZ-12 aggregate to minimise simultaneity issues. This bias should be negligible for smaller economies, but more relevant for bigger countries like France or Germany. The results do not vary significantly, as reported in Belke et al. (2016).
[4] To investigate whether our relationship between the national and the aggregate cycle changed after the eruption of the financial crisis, we included a dummy variable in our empirical model which takes the value of one for the period after 2007Q4 and zero otherwise. The interaction term between this crisis dummy and the EZ12 cyclical component indicates whether there was a trend shift. As reported in more detail in Belke et al. (2016), we do not find big changes, except that the R2 is, with the exception of Italy, always lower for the periphery than for the core countries. These findings are broadly in line with Gogas (2013), but are at odds with De Grauwe and Ji (2016).