What is the relationship between investments and productivity? On the macro level there is a positive correlation between the two, and it is natural to think that higher productivity comes, at least in part, from preceding investment outlays.
The vintage capital model of Cooley et al. (1997) lays the ground for a positive and causal association. It treats investments as technological upgrading, arguing that new capital embodies the more ‘recent’ technology. However, in Jovanovic and Nyarko (1996) and Klenow (1998), productivity increases as firms learn about the new technology. The switch of technologies connected with investment temporarily reduces expertise because technical knowledge is highly specific. It follows that productivity may initially decline when a firm adopts new technology but then rises as employee’s gain experience with the new system(s).
On the firm level, the empirical observations could be diversified – and indeed they are. Empirical studies usually utilise the fact that firm-level investments are lumpy. Years of repair and maintenance are followed by one (or several) periods of heavy investment (Doms and Dunne 1998). It is then also possible to identify productivity effects of these investment spikes. As mentioned, both positive (Geylani and Stefanou 2013) and negative (Sakellaris 2004) effects are found in the data, but the latter are usually small or short-lived.
Identification strategy
In a recent paper (Gradzewicz 2020), I also identify the effects of investment spikes. However, I propose a more precise and robust identification scheme, utilising methods used in social sciences to mimic an experimental research design. I also shed new light on some of the differences present in the existing literature.
Similarly to Grazzi et al. (2016), I identify spikes as events when a firm invests a lot relative to its existing capital, and relative to a ‘normal’ investment schedule of the industry it operates within. The ‘normal’ investment schedule is estimated from the data in a non-parametric non-linear regression of investment rate on log lagged-capital. The model also accounts for the fact that smaller firms (on average) tend to invest more than larger ones.
When assessing the effects of investment spikes, I compare the firms’ performance to a carefully chosen group of ‘statistical twins’. I use matching techniques to find firms that are very similar to the firms with spikes in terms of size, destination market, technology, performance, financing, and which operate in the same industry. As spike events occur in different time periods, I use the sample construction method proposed by Gormley and Matsa (2011) and estimate the size of post-spike performance change using a difference-in-difference estimator. My method guarantees robustness of the results which are not driven either by any particular year or business cycle variation of investment activity (or by any specific set of firms). The results are also robust in the sense that they are estimated on a panel of the census of Polish firms employing ten or more employees, comprising almost all sectors of economic activity.
The impact of investments on TFP
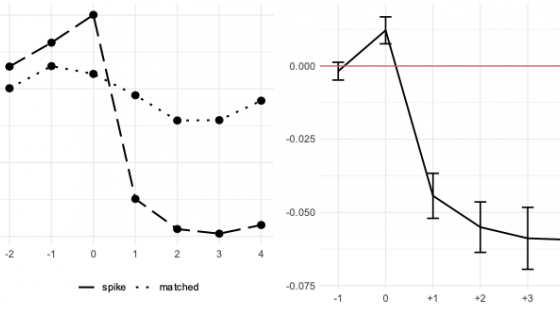
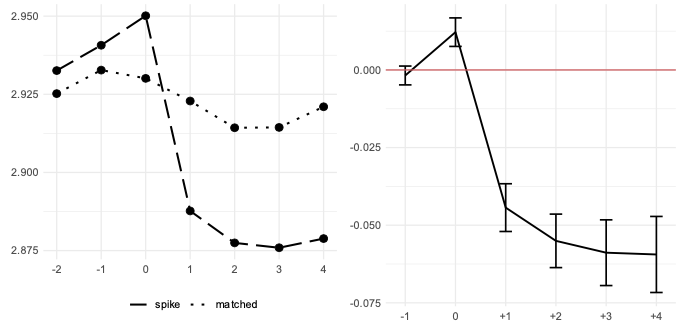
Figure 1 shows one of the main findings: total factor productivity (TFP, measured as in Ackerberg et al. 2015) falls after an investment spike. The left panel presents the evolution of mean levels of log-TFP in both groups of firms with spikes, and of matched ‘statistical twins’ around the spike event (which occurs in period 0). The right panel, in turn, presents the estimated effect, detailing the coefficients from an econometric measurement equation (together with 95% confidence intervals). This shows the difference between the two groups in each period relative to an average difference existing two years before a spike. Ideally, the estimate at t-1 should be insignificant (confirming the parallel trends assumption) and the other estimates should show the immediate effect (at t=0), and the effects for post-spike periods.
Figure 1 Log-TFP: Mean levels (left panel) and coefficients from the diff-in-diff estimation (right panel)
It is evident that after a short rise at the moment of a spike, TFP drops significantly relative to the matched firms, and then levels off six log-points below the TFP level preceding a spike. The fall is persistent. Even four years after a spike, the TFP gap does not evaporate. Therefore, the evolution of TFP is like the trend predicted by Jovanovic and Nyarko (1996) and indicates the existence of ‘learning-by-doing’ effects. The results are also similar to Sakellaris (2004). Moreover, the dynamics of the TFP levels (displayed in the left panel) show that, on average, the TFP of firms with investment spike falls in subsequent periods.
The impact of investments on labour productivity
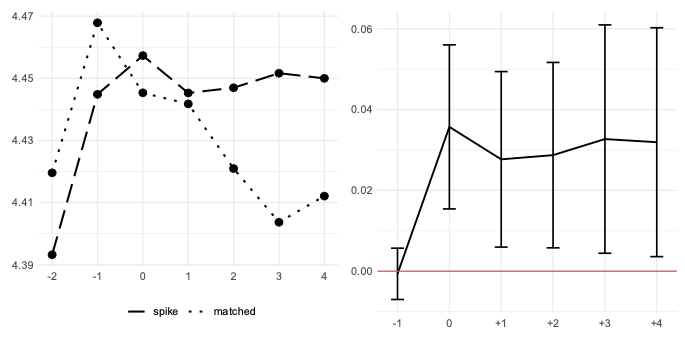
Figure 2 presents analogous results for labour productivity. In contrast to TFP, this relatively simple measure of efficiency improves permanently after an investment spike. The divergence of the two measures of efficiency stems from the fact that labour productivity is an increasing function of TFP and capital deepening (K/L). While the former falls after a spike, the latter rises. This is because investment spikes, by definition, imply an abrupt capital deepening, exerting an upward pressure on labour productivity. This simple observation explains at least part of the divergence in the results found within the existing literature. My analysis also indicates that rising labour productivity after an investment spike is not achieved by scaling down employment. Rather, both output and employment grow after a spike and the former grows faster.
Figure 2 Log labour productivity: Mean levels (left panel) and coefficients from the diff-in-diff estimation (right panel)
Discussion
My recent work provides a deeper analysis of the data properties to verify the results of a technology-learning model outlined by Klenow (1998). However, only some of my findings are consistent with the theoretical model. The learning model implies that when firms learn how to use the new technology relatively quickly, the mean time between spikes is lengthened, and the fall of TFP after a spike is deeper. It follows that a higher learning rate encourages firms to stick with the old technology for longer, meaning they are willing to tolerate a larger TFP drop. My results indicate that the mean time between spikes is longer for larger firms, which employ more skilled labour, and have higher learning capabilities. However, this does not translate into deeper fall of TFP. Moreover, in the learning model the mean time between spikes is lengthened with the persistence and volatility of the demand shocks, whereas in the data the time between spikes tends to decrease with shock volatility, and is not affected by the persistence of shocks.
In summary, I find mixed evidence that the fall of TFP is driven by a learning mechanism. Instead, the responses of sales and efficiency measures seem to suggest that the huge investment activity associated with an investment spike may not be targeted at technology improvement. It is, instead, directed at achieving higher sales and leapfrogging the competitors. Hence, the subsequent fall of TFP can be interpreted as an efficiency cost associated with scaling-up the business. Additionally, we show the positive correlation of responses of labour and K/L in periods after a spike. This implies that these events induce complementarity between production factors. Given the results in Dew-Backer and Gordon (2008) (who showed that labour market reforms induce an increase of employment accompanied by falling productivity), the latter suggests that the sign of employment-productivity relation is conditional on the nature of the shocks. Still, Bessen (2019) showed that positive correlation dominates, citing the case of US manufacturing employment which grew along with productivity for a century or more.
References
Ackerberg, D, K Caves and G Frazer (2015), “Identification Properties of Recent Production Function Estimators”, Econometrica 83(6): 2411–2451.
Bessen, J (2019), “Automation and jobs: When technology boosts employment’, VoxEU.org.
Cooley, T F, J Greenwood and M Yorukoglu (1997), “The replacement problem”, Journal of Monetary Economics 40(3): 457 – 499.
Dew-Backer, I and R J Gordon (2008), “Europe’s employment growth revived after 1995 while productivity growth slowed: Is it a coincidence?”, VoxEU.org,
Doms, M and T Dunne (1998), “Capital Adjustment Patterns in Manufacturing Plants”, Review of Economic Dynamics 1(2): 409–429.
Geylani, P C and S E Stefanou (2013), “Linking investment spikes and productivity growth”, Empirical Economics 45(1): 157–178.
Gormley, T A and D A Matsa (2011), “Growing Out of Trouble? Corporate Responses to Liability Risk”, The Review of Financial Studies 24(8): 2781–2821.
Gradzewicz, M (2020), “What Happens After an Investment Spike—Investment Events and Firm Performance”, Journal of Business and Economic Statistics.
Grazzi, M, N Jacoby and T Treibich (2016), “Dynamics of investment and firm performance: Comparative evidence from manufacturing industries”, Empirical Economics 51(1): 125–179.
Jovanovic, B and Y Nyarko (1996), “Learning by Doing and the Choice of Technology”, Econometrica 64(6): 1299–1310.
Klenow, P J (1998), “Learning Curves and the Cyclical Behavior of Manufacturing Industries”, Review of Economic Dynamics 1(2): 531–550.
Sakellaris, P (2004), “Patterns of plant adjustment”, Journal of Monetary Economics 51(2), 425 – 450.