A large literature has analysed the link between central bank independence (CBI) and inflation. Various approaches have been pursued to this end. One treats countries as units in linear regressions of inflation on a CBI index, controlling for economic and political variables. While numerous studies have found that central bank independence lowers inflation (Cukierman et al. 1992, Arnone and Romelli 2013, Garriga and Rodriguez 2019), others did not find support for such a relationship (Cargill 1995, Campillo and Miron 1997). Some authors argue that this effect depends on the level of political institutions (Acemoğlu et al. 2008), is only visible during specific time periods (Klomp and de Haan 2010) or only in developed countries (Alpanda and Honig 2014).
Despite ambiguous empirical evidence, a consensus grew around the benefits of central bank independence to promote inflation stability (Cukierman 2007, Kern et al. 2019). However, since the Global Crisis, the question has arisen whether central bank independence has come under threat (Masciandaro and Romelli 2015, de Haan and Eijffinger 2017, Goodhart and Lastra 2018).
Reasons for empirical ambiguity
One reason for inconclusive empirical evidence is attributable to the estimation method. Since the problem is longitudinal in nature, a panel setup is more suitable than just simple cross-sectional regressions. Another critical issue concerns the direction of causality. Several authors have recurred to instrumental variable approaches but have been unable to find strong instruments (Crowe and Meade 2008, Jácome and Vázquez 2008). It has been shown repeatedly that standard regression approaches are typically not suitable to answer causal questions, particularly when the setup is longitudinal and when the time-dependent confounders of the outcome-intervention relationship are affected by previous intervention decisions (Daniel et al. 2013).
Longitudinal targeted maximum likelihood estimation (LTMLE)
In recent work (Baumann et al. 2021), we examine the effect of central bank independence on inflation by using a causal model that summarises the economic process of inflation to inform our statistical analysis in which countries are treated as units in a panel setup. Specifically, we employed modern doubly robust effect estimators, i.e. longitudinal targeted maximum likelihood estimators. The estimation procedure incorporates machine learning algorithms and is tailored to address the challenges associated with complex panel macroeconomic data. To describe and address relevant confounding structures, we account for possible reasons that motivate the decision of a country to adopt a certain degree of central bank independence; they range from a country’s political institutions, political instability, inflation history, and international pressure. The intervention variable is the CBI index provided by Dincer and Eichengreen (2014). Further, we have 17 measured variables, including money supply, energy prices, economic openness, institutional variables such as central bank transparency and monetary policy strategies, and political variables. The data underlying our estimations run from 1998 to 2010 and include 60 countries at different stages of development.
Causal inference
Using causal inference in economics has a long history, starting with path analyses and potential outcome language (Tinbergen 1930, Wright 1934) and continuing with regression discontinuity analyses (Hahn et al. 2001), instrumental variable designs (Imbens 2014), and propensity score approaches (Rosenbaum and Rubin 1983). Recently, the use of doubly robust techniques has been proposed in econometrics (Chernozhukov et al. 2018). From the perspective of statistical inference, this is very promising because the use of modern machine learning methods in the estimation of causal effects appear obvious in areas of research characterised by a large number of covariates and complex data-generating processes (Schomaker et al. 2019).
There are three main hurdles that hinder the immediate application of doubly robust effect estimation to macroeconomic data. First, economic processes are complex in the sense that they are often non-linear, time-dependent, and exhibit various interactions between variables. In other disciplines, where doubly robust effect estimation were successfully implemented, e.g. in epidemiology (Schomaker et al. 2019, Bell-Gorrod et al. 2019), these coherences are often simpler. This prevents a direct transition to other disciplines, such as macroeconomics. Second, in order to build a causal model, a thorough review of a vast amount of literature is needed, economic feedback loops need to be incorporated and transmission cycles of policy interventions need to be taken appropriately into account. Third, even after a causal model has been developed, identification of an estimand established, and data collected, statistical estimation may be nontrivial given the complexity of the data set. Official data might not be available for a large number of countries and over a long time span and exhibit a substantial share of missing values. As a result, recommended estimation techniques fail, which calls for the development of an appropriate set of learning and screening algorithms accompanied by a suitable incorporation of the missing mechanism. The benefits of longitudinal targeted maximum likelihood estimation (LTMLE), which is characterised by doubly robust effect estimation in conjunction with machine learning to reduce the chance of model misspecification, can be best utilised under a good and broad selection of learners that are tailored to the problem of interest.
A directed acyclic graph (DAG)
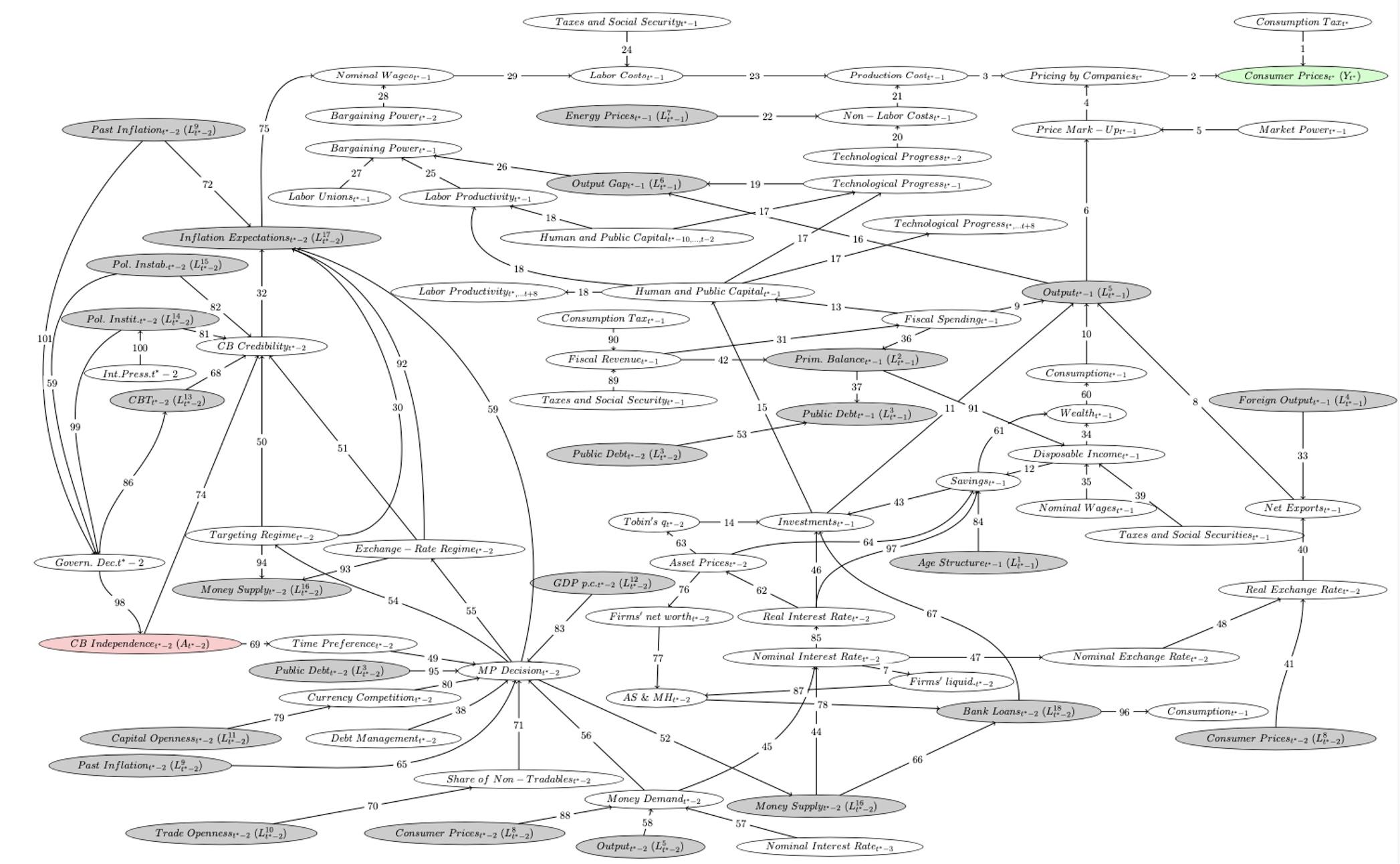
The causal model underlying our analysis is summarised in a directed acyclic graph (DAG) and is exhibited in Figure 1. In this graph, we assume that each variable may be affected only by variables measured in the past and not by those measured in the future. In addition, we make several assumptions regarding the data-generating process. The DAG contains both measured variables (in grey colour) and unmeasured variables (in white colour). The outcome variable is coloured in green, and the intervention in red. It summarises the transmission channels of monetary policy with the focus on causal pathways through which central bank independence can ultimately affect the inflation rate with a time lag, which we assume to be two years. For instance, an independent central bank sets its policy tools autonomously to achieve its objective(s). Since it is less pressured to pursue an overly expansionary monetary policy, it commands higher credibility (arrow 74), which, in turn, keeps inflation expectations at bay (arrow 32), lowers the demands for nominal wage compensation (arrow 75), keeps labour costs (arrow 29), production costs (arrow 23), and companies' prices (arrow 3) low. As a result, consumer prices will be low (arrow 2). This way of encoding a causal model not only offers a promising alternative way to tackle causal questions in economics but also provides a visual overview of the assumptions underlying the analysis. Viktor Chernozhukov, Co-Editor of The Econometrics Journal, argued in a tweet posted on 7 June 2021 that “[t]he DAG-based view on structural and causal inference is under-represented in econometrics…”,1 an imbalance he intends to remedy.
Figure 1 The directed acyclic graph which represents the economy underlying the analysis of Baumann et al. (2021)
Evidence
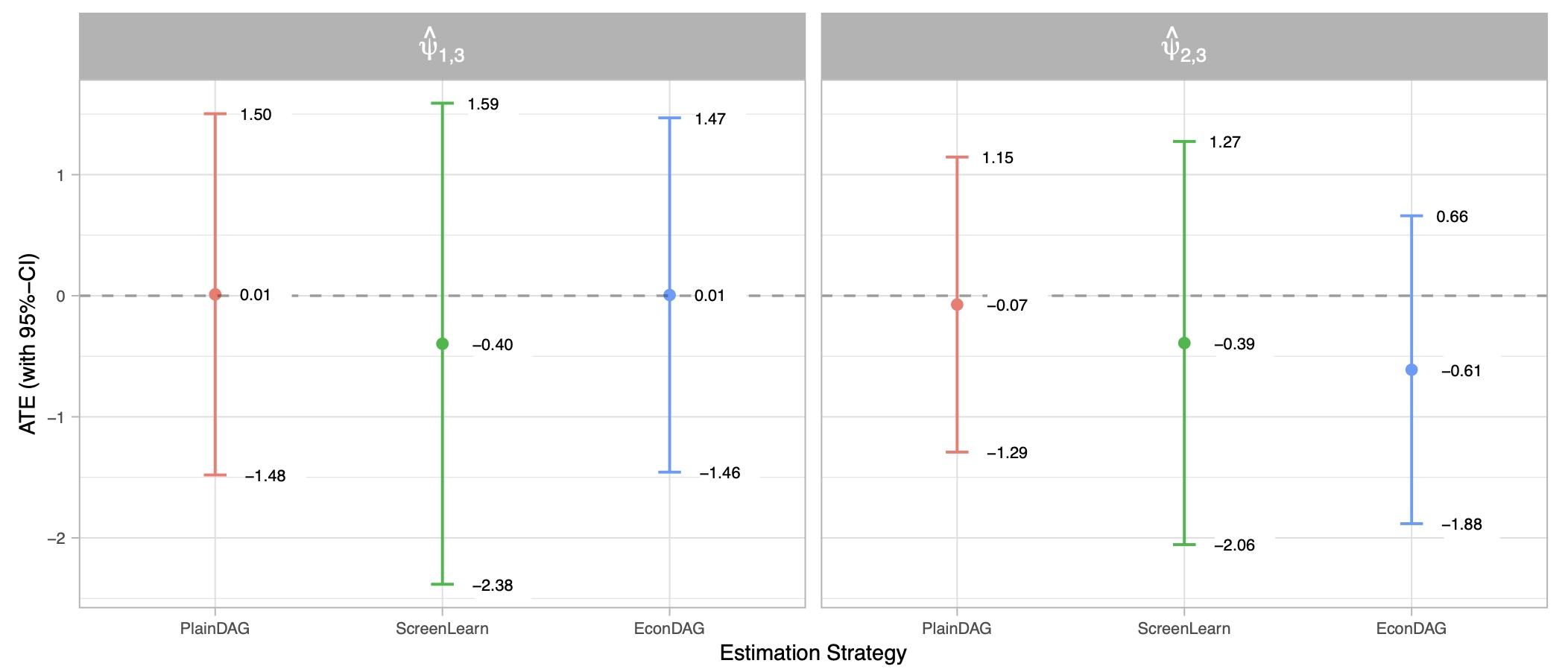
Our main analysis, which is summarised under the label PlainDAG in Figure 2, suggests that if a country had legislated central bank independence for every year between 1998 and 2008, it would have had an average increase in inflation of 0.01 (95% confidence interval: -1.48, 1.50) percentage points in 2010. The first and most important result is that an independent central bank does not necessarily have an effect on inflation. We do not find compelling support for the hypothesis that having an independent central bank for a long period of time necessarily lowers inflation. Similarly, if a country had legislated an independent central bank for every year when the median of the past seven years of inflation had been above 5% or below 0% from 1998 to 2008, it would have led to an average reduction in inflation of -0.07 percentage points only (95% confidence interval: -1.29, 1.15) in 2010 compared to a dependent central bank for the same time span. The other two approaches, ScreenLearn and EconDAG, make different/fewer causal assumptions. The results suggest somewhat stronger reductions of inflation caused by higher central bank independence (up to -0.61 percentage points).
Our findings can be summarised as follows. First, depending on the degree of imposition of structural assumptions, we obtain either a negative effect or no effect on inflation from higher central bank independence, pointing to pitfalls associated with improper causal models/structural assumptions. Second, as suggested by the wideness of the confidence intervals, we can exclude neither a strong negative nor a strong positive average treatment effect (ATE).
Figure 2 Average treatment effect based on a comparison between two static interventions
Notes: Average treatment effects (ATE) based on a comparison between two static interventions (left panel) and a static and a dynamic intervention (right panel) obtained from estimations on the full sample (Baumann et al. 2021).
Sensitivity
For a sensitivity analysis we stratified our sample according to the World Bank's income classification into high-income and low-income countries and repeated the analysis. Sample sizes are considerably reduced and advise caution in interpreting the results. That being said, in the main analysis in high-income countries we obtain an ATE of 0.48. It means that inflation is nearly half a percentage point higher after ten years of central bank independence. For the group of low-income countries, where inflation has typically been higher, we obtain no effect. These findings are quite different from what has been reported in the literature.
Conclusions
In this column we make two contributions. First, we show that central bank independence has no clear effect on inflation; even an inflation-increasing impact cannot be excluded. In this sense, our findings capture the ambiguity reported in the literature. Second, from a methodological perspective, we show that even for complex macroeconomic questions it is possible to develop a causal model and implement modern doubly robust longitudinal effect estimators. This is important in light of the ongoing debate on the appropriate implementation and use of causal inference for economic questions (Imbens 2019). Both the causal model and the estimation techniques we propose have not been used in tackling economic problems. We are quite confident that both will be useful in examining other relevant questions typically posed by economists.
Authors note: The views, opinions, findings, and conclusions or recommendations expressed in this column are strictly those of the authors. They do not necessarily reflect the views of the Swiss National Bank (SNB). The SNB takes no responsibility for any errors or omissions in, or for the correctness of, the information contained in this column.
References
Acemoğlu, D, S Johnson, J Robinson and P Querubin (2008), “When does policy reform work? The case of central bank independence”, VoxEU.org, 25 June.
Alpanda, S and A Honig (2014), “The impact of central bank independence on the performance of inflation targeting regimes", Journal of International Money and Finance 44: 118–135.
Arnone, M and D Romelli (2013), “Dynamic central bank independence indices and ination rate: A new empirical exploration", Journal of Financial Stability 9(3): 385–398.
Baumann, P F M, M Schomaker and E Rossi (2021), “Estimating the Effect of Central Bank Independence on Inflation Using Longitudinal Targeted Maximum Likelihood Estimation”, Journal of Causal Inference 9(1): 109–146.
Bell-Gorrod, H, M P Fox, A Boulle, H Prozesky, R Wood, F Tanser, M A Davies and M Schomaker (2019), “The impact of delayed switch to second-line antiretroviral therapy on mortality, depending on failure time definition and cd4 count at failure", bioRxiv.
Campillo, M and J A Miron (1997), “Why Does Inflation Differ across Countries?”, In C D Romer and D H Romer (eds.), Reducing Inflation: Motivation and Strategy, p. 335–362, University of Chicago Press.
Cargill, T (1995), “The statistical association between central bank independence and inflation", BNL Quarterly Review 48(193): 159–172.
Chernozhukov, V, D Chetverikov, M Demirer, E Duflo, C Hansen, W Newey and J Robins (2018), “Double/debiased machine learning for treatment and structural parameters", The Econometrics Journal 21(1): C1–C68.
Crowe, C and E E Meade (2008), “Central bank independence and transparency: Evolution and effectiveness", European Journal of Political Economy 24(4): 763–777.
Cukierman, A (2007), “The central bank independence revolution”, VoxEU.org, 27 September.
Cukierman, A, S B Webb and B Neyapti (1992), “Measuring the independence of central banks and its effect on policy outcomes", The World Bank Economic Review 6(3): 353–398.
Daniel, R M, S N Cousens, B L De Stavola, M G Kenward and J A Sterne (2013), “Methods for dealing with time-dependent confounding", Statistics in Medicine 32(9): 1584–618.
De Haan, J and S C W Eijffinger (2017), “Central bank independence under threat?”, CEPR Policy Insight No 87.
Dincer, N N and B Eichengreen (2014), “Central bank transparency and independence: Updates and new measures", International Journal of Central Banking 10(1): 189–259.
Garriga, A C and C M Rodriguez (2019), “More effective than we thought: Central bank independence and inflation in developing countries”, Economic Modelling 85: 87-105.
Goodhart, C and R Lastra (2018), “Potential threats to central bank independence”, VoxEU.org, 11 March.
Hahn, J, P Todd and W Van der Klaauw (2001), “Identification and estimation of treatment effects with a regression-discontinuity design", Econometrica 69(1): 201–209.
Imbens, G (2014), “Instrumental variables: An econometrician's perspective", Statistical Science 29(3): 323–358.
Imbens, G (2019), “Potential outcome and directed acyclic graph approaches to causality: Relevance for empirical practice in economics”, NBER Working Paper 26104.
Jácome, L I and F Vázquez (2008), “Is there any link between legal central bank independence and inflation? Evidence from Latin America and the Caribbean", European Journal of Political Economy 24(4): 788–801.
Kern, A, B Reinsberg and M Rau-Göhring (2019), “IMF conditionality and central bank independence", European Journal of Political Economy 59(C): 212–229.
Klomp, J and J de Haan (2010), “Inflation and central bank independence: a meta-regression analysis", Journal of Economic Surveys 24(4): 593–621.
Masciandaro, D and D Romelli (2015), “Central bank independence before and after the Great Recession”, VoxEU.org, 28 August.
Rosenbaum, P and D Rubin (1983), “The central role of the propensity score in observational studies for causal effects", Biometrika 70(1): 688–701.
Schomaker, M, M A Luque-Fernandez, V Leroy and M A Davies (2019), “Using longitudinal targeted maximum likelihood estimation in complex settings with dynamic interventions", Statistics in Medicine 38(24): 4888–4911.
Tinbergen, J (1930), “Determination and interpretation of supply curves: an example", Zeitschrift für Nationalökonomie 1: 669–679.
Wright, P (1934), “The method of path coefficients", The Annals of Mathematical Statistics 5: 161–215.
Endnotes
1 https://twitter.com/VC31415/status/1401694440062865416