Many economically relevant decisions are complex. Consider the decision of how much of your money to invest in the stock market. Rational decision-making requires you to combine your attitudes towards risk with your expectations about how the stock market will evolve in the future. Yet, these considerations are difficult. What is your level of risk aversion? How exactly do you combine your level of risk aversion with your expectations about the future performance of the market? How should you form these expectations to begin with? What is the information that you had until today, and how do you incorporate the latest announcement by the central bank?
Because these components of decision-making are all difficult, people might be unsure how exactly they should behave. Crucially, people are often aware that they do not really know what the optimal thing to do is. This is what we label cognitive uncertainty: subjective uncertainty about the optimal action.
How does such cognitive uncertainty, which is absent in traditional models of economic decision-making, affect behaviour? Does it help us better understand established anomalies in behavioural economics?
Recent models of cognitive noise, i.e. the idea that we reason imprecisely, propose that when people are unsure about what is right, they rely on some default set of parameter values (Woodford 2019, Gabaix 2019). A key implication of this idea is that cognitive noise and bias are linked: when people are cognitively uncertain, they revert more to a mental default, which introduces systematic bias.
In the stock market example above, the processing of probabilities plays a crucial role. A plausible conjecture is that when people do not quite understand the decision environment, they treat all uncertainty as if it reflects 50:50 odds. For example, when in April 2011, intelligence officers told Barack Obama that there was a 30% to 95% probability that Osama bin Laden was in the Abbottabad compound in Pakistan, he responded: “This is 50:50. Look guys, this is a flip of the coin.” Obama took a set of complex probabilistic information to mean the same as 50:50. In this case, it becomes obvious that 50:50 expresses a form of ignorance and essentially means “I don’t know”.
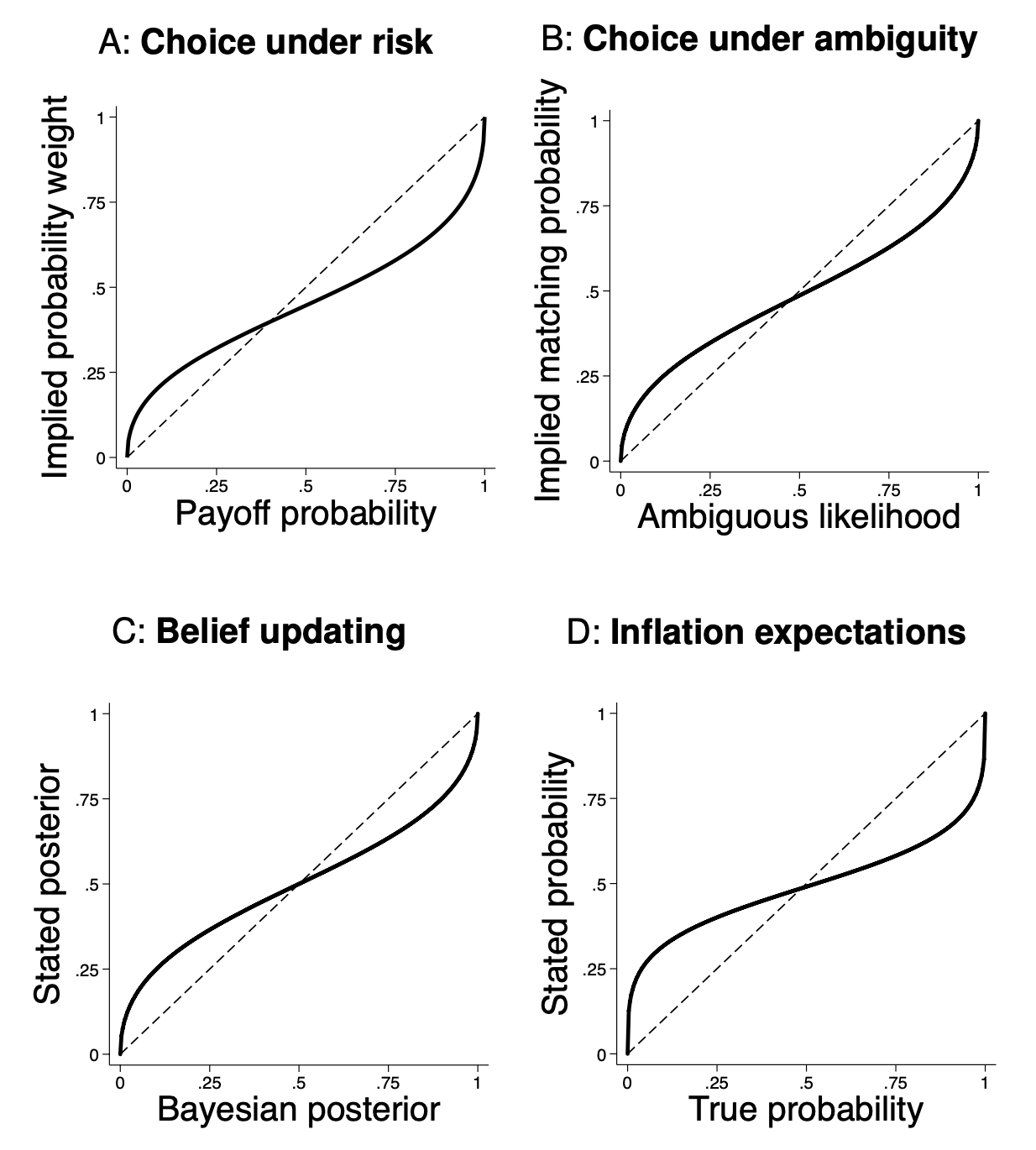
Puzzle: Inverse S-shaped weighting functions across different decision domains
In Enke and Graeber (2020), we study the effect of cognitive uncertainty on economic behaviour and belief formation as it relates to probabilities. Figure 1 illustrates four well-established anomalies that our paper attempts to explain. While each of these four anomalies has individually been shown to explain economic behaviour in practice, they are considered distinct phenomena and studied in separate literature.
Figure 1 ‘Weighting functions’ in choices and beliefs
All four functions are estimated from experimental data and share a characteristic inverse S-shape of subjective with respect to objective probabilities.
First, panel A depicts the well-known probability weighting function in choice under risk that goes back to Tversky and Kahneman (1992). It illustrates how experimental subjects implicitly treat objective probabilities in choosing between different monetary gambles.
Second, panel B depicts an ‘ambiguity weighting function’ that reflects the emerging consensus that people are ambiguity-averse for likely gains, yet ambiguity-seeking for unlikely gains. This reflects a compression effect that is called ‘a-insensitivity’ in the literature.
Third, in panel C, we illustrate a less well-known stylised fact: an inverse S-shaped relationship between participants’ posterior beliefs and the Bayesian posterior in canonical ‘balls-and-urns’ belief updating tasks of the type recently reviewed by Benjamin (2019).
Finally, panel D shows the relationship between objectively correct probabilities and respondents’ subjective probabilistic estimates about, e.g. stock market returns, inflation rates, or the shape of the income distribution. Here, again, people’s beliefs are compressed towards 50:50.
Why do these four functions, drawn from different decision contexts and experimental paradigms, look so strikingly similar?
In Enke and Graeber (2020), we test the hypothesis that these behavioural anomalies are all generated by cognitive uncertainty. As in the Obama example, people who are cognitively uncertain about how to deal with probabilities between two choices (i.e. a binary state) implicitly treat them as if they were closer to 50% than they really are.
Our formal framework makes three predictions. First, in the presence of cognitive noise, people should be cognitively uncertain when they deal with probabilities: they should have an awareness that they do really know how to behave optimally in the contexts described above.
Second, people who exhibit higher cognitive uncertainty should exhibit more compressed ‘weighting functions’ in all decision domains above. Intuitively, this should be the case because a higher level of cognitive uncertainty induces people to tend more towards probabilities of 50:50.
Third, by the same logic, exogenously increasing cognitive uncertainty should lead people to make decisions that reflect a higher degree of compression of probabilities.
Measuring cognitive uncertainty and linking it to economic decisions
We make an individual’s cognitive uncertainty visible in a structured way and link it to economic decisions and beliefs. The idea is to allow participants to indicate an interval of possible responses such that they are certain that their optimal response is contained within that interval.
On the one hand, if an individual is subjectively fully certain that a given action is optimal, they would state a degenerate interval. Cognitively uncertain people, on the other hand, may be unsure whether their certainty equivalent for a 70% chance of winning $20 is actually $13 or whether it could be anywhere between $11 and $15, for example. This ‘not knowing a certainty equivalent’ does not exist in standard models of decision-making.
We elicit structured measurements of cognitive uncertainty in standard decision tasks that measure participants’ attitudes towards risk and ambiguity, their belief updating process in so-called balls-and-urns updating tasks, and their forecasts of future economic variables such as the inflation rate.
In contrast to the predictions of all economic models that do not feature cognitive noise, a large fraction of participants indicate strictly positive levels of cognitive uncertainty across decision domains. Moreover, an individual’s cognitive uncertainty reflects some stability across task domains: we find that people who are cognitively uncertain in choices between lotteries are also cognitively uncertain about their forecasts of economic variables.
How does this heterogeneity in cognitive uncertainty manifest in economic behaviours? Our main hypothesis is that the amount of cognitive uncertainty is associated with the degree of compression (inverse S-shape) in the response functions depicted in Figure 1. Our results consistently show a relationship between cognitive uncertainty and compression across all four domains of decision-making.
Figure 2 shows this pattern for the well-known probability weighting function. Participants with higher cognitive uncertainty exhibit more pronounced weighting functions, meaning that they are more risk-seeking for low-probability gains but more risk-averse for high-probability gains.
Figure 2 Probability weighting separately for low and high cognitive uncertainty subjects
Similarly, Figure 3 shows that cognitive uncertainty is strongly predictive of belief updating in canonical balls-and-urns updating tasks. Here, participants with high cognitive uncertainty state beliefs that are far too high whenever the Bayesian posterior is below 50%. By the same token, these participants state beliefs that are too low whenever the Bayesian posterior is above 50%.
Figure 3 Reported beliefs as a function of Bayesian posteriors separately for low and high cognitive uncertainty subjects
It is noteworthy that these results for belief updating and choices among risky lotteries are visually strikingly similar even though they stem from distinct choice domains.
The patterns discussed so far are all correlational; we go a step further by exogenously manipulating cognitive uncertainty and the location of the mental default. With respect to the former, once cognitive uncertainty increases for exogenous reasons, the probability weighting function or stated beliefs in balls-and-urns updating tasks should exhibit more pronounced compression towards 50:50.
To test this hypothesis, we manipulate cognitive uncertainty by introducing compound problems. We find that in compound problems, measured cognitive uncertainty indeed increases substantially, and subjects’ responses become substantially more compressed towards implicit probabilities of 50%. This suggests that the relationship between cognitive uncertainty and choices is indeed causal.
In summary, cognitive uncertainty is a measurable concept that allows us to bring together, and partially explain, seemingly-unconnected anomalies from decision tasks on choice under risk and ambiguity, belief updating, and survey expectations. We believe that the concept of cognitive uncertainty is likely to be important also outside of the domain of probabilities that we study in our paper. After all, many economic decisions are highly complex, even when they do not involve probabilities.
By providing a simple and portable experimental tool that allows measuring cognitive uncertainty in a quantitative fashion, our paper opens up the possibility for future experimental work on the relationship between cognitive uncertainty and economic decision-making.
References
Benjamin, D J (2019), “Errors in probabilistic reasoning and judgment biases”, Handbook of Behavioral Economics: Applications and Foundations 1(2): 69–186.
Enke, B, and T Graeber (2019), “Cognitive uncertainty”, NBER w26518.
Gabaix, X (2019), “Behavioral inattention”, Handbook of Behavioral Economics: Applications and Foundations 1(2): 261–343.
Tversky, A, and D Kahneman (1992). “Advances in prospect theory: Cumulative representation of uncertainty”, Journal of Risk and uncertainty 5(4): 297–323.
Woodford, M (2019), “Modeling imprecision in perception, valuation and choice”, NBER w26258.