In a bank's solvency ratio, the denominator is made up of risk-weighted assets. As solvency ratios are the core part of modern banking regulation, the precise way that risks are weighted is crucial to the success of banking supervision.
Basel II permitted banks to use an internal ratings-based (IRB) approach. This means they can use internal risk models to quantify their capital requirements for credit risk. Basel II also allows banks to employ a simpler standardised approach (StA) for calculating their credit risk, which is mainly used by smaller banks.
By giving permission to use internal risk estimates, regulators aimed to increase the risk sensitivity of capital requirements. However, banks have had an incentive to use artificially low internal estimates of risk. The gap between bank and supervisory standards for risk models, and the increase in complexity of these models, has created a policy debate in which the US is sceptical of risk weights, while the EU is in favour of them.
Research into whether supervisors could prevent banks from embellishing capital ratios has found discrepancies in risk weights across banks and jurisdictions. Examples include Behn et al. (2016), Vallascas and Hagendorff (2013), Mariathasan and Merrouche (2014), and Bruno et al. (2016).
International bodies like the Basel Committee on Banking Supervision (BCBS) and the European Banking Authority (EBA) responded to this by strengthening their focus on the topic. Some (Haldane 2012, for example) argue that banking regulation should become less complex. This view has attracted growing support recently (BCBS 2016b).
With the transition to IFRS 9, internal credit risk models will also be used to determine credit risk provisions. This means the comparability of the outcomes given by internal bank models is more relevant than ever.
In a recent paper (Döme and Kerbl 2017), we ask to what extent differences in risk weights can be explained by factors that relate to credit risk – as regulators intend – and what extent by unintended factors, like the location of the bank headquarters (and thus its main supervisor).
The response to risk weight heterogeneity
Regulatory reviews have begun to address this issue. The Regulatory Consistency Assessment Programme (RCAP) exercise of the BCBS, the EBA’s review of consistency of risk-weighted assets exercise, and the ECB’s Targeted Review of Internal Models (TRIM) exercise are all examples. According to the EBA’s benchmarking report (EBA 2017a), for example, the country of the reporting bank and the respective countries of the counterparties are important drivers of risk weight variability.
Action as well as words show this topic is taken seriously by regulators. For example, in many countries macroprudential supervisors have established risk weight floors (ESRB 2017).
Exploring risk weight heterogeneity in Europe
Our analysis is based on the datasets from the EBA transparency exercises. This public database is made up of bank-specific data from more than 130 banks, in 24 countries in Europe. This represents around 70% of total EU banking assets (European Banking Authority 2015).
The dataset has the advantage of granularity – exposures and risk weight are broken down by banks, asset classes, destinations of the credit and calculation method (IRB versus standardised approach), as well as time. This granularity allows us to compare portfolio-by-portfolio risk weight determined by a number of factors.
Risk weights based on standardised and IRB approaches are different
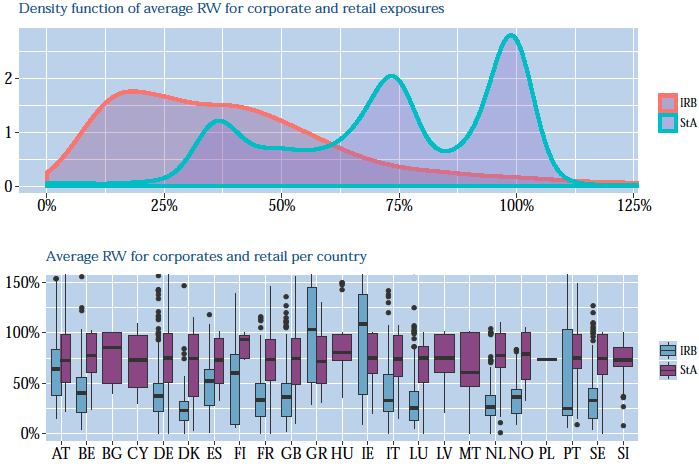
The upper panel of Figure 1 shows kernel density estimates for risk weights for retail and corporate clients, calculated under the StA and IRB approaches. The lower panel is a breakdown by the country of the consolidating entity (in other words, the country in which a bank is headquartered, which we will refer to as 'HQ country'). IRB weights are substantially lower than StA weights. The StA weights have a very similar distribution, but IRB weights vary substantially from country to country.1
Figure 1 Distribution of risk weights for corporate and retail exposures
Source: EBA transparency exercise and author calculations.
Determinants of IRB risk weights
From the lower panel of Figure 1 we infer that there are large country differences between IRB risk weights. We estimate a panel model that includes country-, bank-, and portfolio-specific factors as control variables to investigate whether we can explain these differences by differences in the underlying risk. More precisely we use:
- The asset class – credit to an institution tends to be less risky than to small corporates
- A set of macroeconomic variables – for example, recent GDP growth specific to the destination of the credit
- The ratio of non-performing loans in that portfolio2 – the NPL ratio is an excellent indicator of the riskiness of the particular portfolio and is available on the same level of granularity as risk weights (bank-asset class-time and destination basis)
- Further portfolio-specific factors – for example, whether the credit is to a foreign country, the relevance of the particular market to the bank, and the NPL ratio of the whole asset class of that bank
- Hidden destination-specific effects – these are captured by dummy variables
This set of factors, which reflect intended risk weight variability, explains 56% of risk weight variance.
After controlling for risk, we investigate whether different implementation standards and supervisory practices (unintended risk weight heterogeneity) also matters. For this purpose, we add dummies for each country in which the bank granting the loan is headquartered. In an ideal world with equal implementation standards, these HQ fixed effects would be statistically zero.
When we do this, the explained variance rises only to 57%. But the HQ effects are important.3
These statistically significant and economically important effects (in line with Turk-Ariss 2017 and EBA 2017a) are large in Denmark, Sweden, and Italy, where banks have low risk weights. The opposite is true in Ireland, UK, Portugal and Austria. For example, the expected IRB risk weight of a bank headquartered in Italy is 18.3 percentage points lower than the IRB risk weight of a Portuguese bank with the same destination, asset class, and macroeconomic environment. Note that some of these identified countries have already taken macroprudential measures targeting bank risk weights (ESRB 2017).
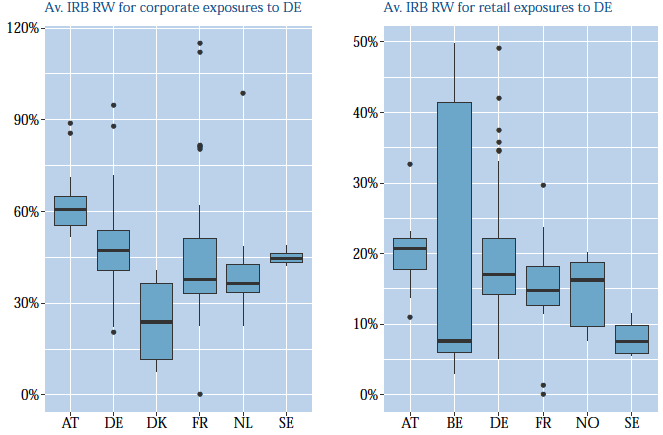
Figure 2 depicts risk weights pertaining to the same asset class and the same destination (Germany) of all banks headquartered in selected countries. Germany was chosen as a destination because a large number of banks from different HQ countries actively grant loans to Germany, which enables us to draw this comparison. The HQ countries were chosen based on their HQ regression dummy coefficient. While Figure 2 illustrates the heterogeneity across HQ countries, the results in a regression allows us to identify HQ effects after controlling for portfolio-specific NPL ratios.
Figure 2 IRB risk weights for corporate exposures (left) and retail exposures secured by real estate (right)
Source: EBA transparency exercise and author calculations.
The effects of changing HQ countries on a bank's capital ratios
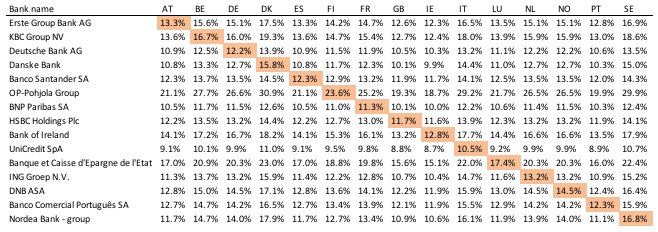
How would capital ratios change if we change only the country where a bank is headquartered and keep everything else equal? For this hypothetical exercise, we select the largest banks from each country and use the estimation results obtained in the previous section to calculate capital ratios.
Clearly, these calculations are hypothetical in several respects, and are not a 'what if' bank A moved its HQ to country B, because risk models that are already improved are unlikely to change abruptly. Table 1 shows the hypothetical capital ratios for the largest banks in all countries. The main diagonal represents actual capital ratios as at June 2016. The off-diagonal elements often deviate from the actual ratios. The effects are economically large.4
Table 1 Hypothetical CET1 ratios of selected banks
Source: author calculations.
Is there unintended risk weight heterogeneity?
We also look at other forms of unintended risk weight heterogeneity, but find no evidence that large banks are better able to outmanoeuvre supervisors by increasing the complexity of their models. We find marginal statistical evidence (p < 0.1) that banks with a low CET1 ratio push for low risk weights.
Enforcing consistent standards
We find that a large share of risk weight variability can be explained by differences in the underlying risk, but there are statistically significant and economically important differences relating to the country in which the bank is headquartered. This provides evidence that standards are implemented differently from jurisdiction to jurisdiction. This finding is robust to a range of alternative specifications.
Recent efforts by supervisors to lower risk weight variability are important, most notably the EBA benchmarking exercise and the ECB’s TRIM exercise. The measures, focusing specifically on the euro area, should be extended to encompass also non-euro area countries in order to reduce unwarranted risk weight variability.
In addition, our results support regulatory floors for risk weights as envisaged under Basel IV, and efforts by supervisors to harmonise banks’ Pillar III requirements. Our findings can inform the ongoing policy debate about the complexity of regulation. Complex rules require great effort – possibly too much effort – from supervisors to enforce standards consistently, and to monitor the banks that are subject to the rules.
Authors’ note: The views expressed in this column are exclusively those of the authors and do not necessarily reflect those of the OeNB or the Eurosystem. The authors would like to thank Markus Behn (ECB) for helpful comments and valuable suggestions.
References
BCBS (2013), “Regulatory consistency assessment programme (RCAP) – Analysis of risk-weighted assets for credit risk in the banking book”.
BCBS (2014), “Capital floors: the design of a framework based on standardized approaches”.
BCBS (2016a), “Reducing variation in credit risk-weighted assets – constraints on the use of internal model approaches”.
BCBS (2016b), "Finalising Basel III: Coherence, calibration and complexity", speech by Stefan Ingves at the second Conference on Banking Development, Stability and Sustainability, 2 December, Santiago, Chile.
Barakova, I and A Palvia (2014), "Do banks’ internal Basel risk estimates reflect risk?", Journal of Financial Stability 13: 167–179.
Begley, T A, A Purnanandam and K Zheng (2017), "The Strategic Under-Reporting of Bank Risk", Review of Financial Studies 30(10): 3376–3415.
Behn, M, R Haselmann and V Vig (2016), The limits of model-based regulation, ECB working paper 1928.
Beltratti, A and G Paladino (2016), "Basel II and regulatory arbitrage. Evidence from financial crisis", Journal of Empirical Finance 39: 180–196.
Bruno, B, G Nocera and A Resti (2016), “Are risk-based capital requirements detrimental to corporate lending? Evidence from Europe”, CEPR Discussion Paper No. 12007.
Döme, S and S Kerbl (2017), Comparability of Basel risk weights in the EU banking sector, Oesterreichische Nationalbank, Financial Stability Report 34: 68-89.
European Banking Authority (2013), "Interim results update of the EBA review of the consistency of risk-weighted assets".
European Banking Authority (2015), 2015 EU-wide transparency exercise, 25 November.
European Banking Authority (2017a), "Results from the 2016 High Default Portfolios (HDP) Exercise", EBA Report BS 2017 027.
European Banking Authority (2017b), "Results from the 2016 Market Risk Benchmarking Exercise", EBA Report BS 2017 031.
European Central Bank (2017), "Guide for the Targeted Review of Internal Models (TRIM) – Counterparty Credit Risk", Banking Supervision, February.
European Systemic Risk Board (2017), “National Policy – Other measures” (retrieved on 17 August 2017).
Fraisse, H, M Le and D Thesmar (2015), “The Real Effects of Bank Capital Requirements”, HEC Paris Research Paper FIN-2013-988.
Haldane, A G (2012), “The Dog and the Frisbee”, speech at the Federal Reserve Bank of Kansas City’s 366th economic policy symposium, “The changing policy landscape”, Jackson Hole, 31 August.
Hastie, T, R Tibshirani and J Friedman (2009), The Elements of Statistical Learning, New York: Springer.
Kerbl, S and M Sigmund (2009), "Cyclicality of Regulatory Capital Requirements: First Evidence from Austria", Financial Stability Report 18: 97–106.
Mariathasan, M and O Merrouche (2014), "The manipulation of Basel risk-weights", Journal of Financial Intermediation 23: 300–321.
Plosser, M C and J A C Santos (2014), “Banks’ Incentives and the Quality of Internal Risk Models”, Federal Reserve Bank of New York Staff Reports 704.
Turk-Ariss, R (2017), “Heterogeneity of Bank Risk Weights in the EU: Evidence by Asset Class and Country of Counterparty Exposure”, IMF Working Paper 17/137.
Vallascas, F and J Hagendorff (2013), "The Risk Sensitivity of Capital Requirements: Evidence from an International Sample of Large Banks", Review of Finance 17(6): 1947–1988.
Endnotes
[1] There are caveats comparing StA risk weights and IRB risk weights, which make a more detailed comparison difficult. But, everything else equal, a bank with a higher share of IRB exposures will tend to have substantially reduced RWA.
[2] Strictly speaking, for the ratio of NPLs, we used the ratio of defaulted loans (as included in our dataset). There is a slight difference between NPLs and defaulted loans.
[3] The probability that all HQ effects are equal to zero can be rejected at any probability level (F-statistic: 228.5 on 16 and 7,670 degrees of freedom). The R2 of using solely HQ effects, and no other regressors, would be 32%. We conducted further statistical tests and robustness checks that validate this conclusion.
[4] We additionally validated this finding by training a random-forest and a boosted regression tree to our data, as well as using a large set of different regression setups.