The level of global real economic activity is a crucial variable in many economic models. For empirical analysis of the determinants of variables like commodity prices, interest rates, or exchange rates, researchers often need a monthly measure of economic activity. One interesting idea is to use a market price such as the cost of shipping as a proxy for the level of global real economic activity.
To get a series going back to 1968, Kilian (2009) collected growth rates for a set of individual shipping costs for a given month t and then took an average of the growth rates available for that month. Accumulating the average monthly growth rates over time gave him a nominal index of shipping prices. He then divided this index by the level of the US consumer price index and regressed the log of this ratio on a deterministic time trend to isolate a cyclical component of real shipping costs. The residuals from this regression have been used in dozens of prominent economic studies as a monthly measure of global real economic activity.1 Kilian and Zhou (2018) recently summarised a number of reasons why this might still be a good measure to use.
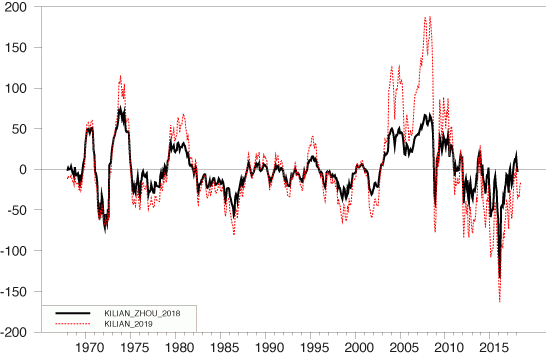
Although accumulating the growth rates of shipping costs produces a nominal index, the index is measured not in units of dollars but instead in the natural logarithm of dollars. I observed that it therefore does not make sense to divide this index by the CPI (Hamilton 2019). Moreover, when Kilian (2009) took the log of the ratio, the operation effectively amounted to taking logs twice, giving the series some undesirable properties. Upon seeing my analysis, Kilian (2019) agreed with the criticism and now recommends subtracting the log of the CPI from the original index and then regressing this difference directly on a deterministic time trend. Figure 1 compares the measure used in the studies listed in footnote 1 (in black) with the series that Kilian now recommends (in red).
Figure 1 Comparison of the measures used by Kilian and Zhou (2018) and Kilian (2019)
Notes: Black: series downloaded from Kilian’s webpage July 2018. Dotted red: series downloaded from Kilian’s webpage April 2019.
Source: Hamilton (2019).
A primary motivation given by Kilian (2009: 1057) for using shipping costs as a measure of global real economic activity came from an anecdotal review of global developments over 1970-2007. He concluded that the new index “is fully consistent with the anecdotal evidence on the relative importance and timing of these fluctuations in global real economic activity.”
Applying that same standard to the more recent values of either index in Figure 1 raises substantial doubts about the measures’ continuing reliability. The series claim that the cyclical component of world economic activity fell to a far lower level in 2016 than was realised in either the financial crisis of 2008-2009 or the 1974-75 global recession. That conclusion seems hard to justify on the basis of GDP data for any major country, and certainly is inconsistent with the assertion in Kilian (2009: 1056) that “the level of global real economic activity as it relates to industrial commodity markets is proportionate to this index.”
It is straightforward to test whether the real cost of shipping (calculated either as Kilian originally proposed or as he now recommends) is characterised by a deterministic time trend.2 Augmented Dickey-Fuller tests (e.g. Hamilton 1994) and the tests of Kwiatkowski et al. (1992) suggest that real shipping costs are better characterised as a process subject to persistent shocks, rather than a series that is stationary around a fixed time trend. If that is correct, it means that the series in Figure 1 have some spurious features.
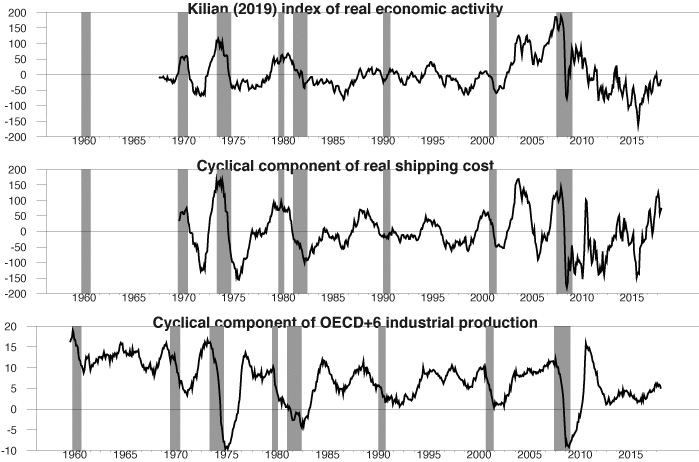
In a previous paper (Hamilton 2018), I proposed an approach to isolating the cyclical component that works well for most macroeconomic time series. The proposal is to take the difference between the value of the series in month t and its value two years earlier. This measure of the cyclical component of real shipping costs is compared with that proposed by Kilian (2019) in the top two panels of Figure 2.
The reason that Kilian’s measure regards 2016 as the worst downturn in record is in part because a linear trend was used to construct it. The measure in the second panel, which does not assume a linear time trend, would still describe 2016 as a severe contraction, but not worse than the Global Crisis.
Figure 2 Alternative measures of global real economic activity
Notes: Top panel: measure used by Kilian (2019), 1968:1-2018:6, obtained by downloading the real activity measure from Kilian’s webpage in April 2019. Middle panel: cyclical component of real shipping costs, as calculated from the two-year change in 100 times the natural logarithm of the real cost of shipping. Result is plotted for 1970:1-2018:6. Bottom panel: cyclical component of world industrial production, as calculated by the two-year change in 100 times the natural logarithm of the industrial production index for OECD plus 6 major countries. Result is plotted for 1960:1-2018:6. Shaded regions denote NBER US recession dates.
Source: Hamilton (2019).
One of the arguments given by Kilian and Zhou (2018) against using a series like world GDP is that the latter is only available quarterly, and even then for a relatively short sample. One obvious check is to regress the annual growth rate of world real GDP for year τ (available annually, well before Kilian’s index begins) on a proposed measure of the cyclical component of global real economic activity as it was reported in December of that year. In my paper (Hamilton 2019), I found that the measures proposed by Kilian have R2 below 4% in terms of explaining annual GDP growth and are not statistically significant. By contrast, the measure in the middle panel of Figure 2 explains 23% of the variance and is highly significant.
An index of global industrial production offers an obvious alternative to shipping costs as a monthly measure of real economic activity. OECD Main Economic Indicators published an estimate of monthly industrial production for the OECD plus 6 other major countries (Brazil, China, India, Indonesia, the Russian Federation and South Africa). The OECD series begins in January 1958 and ends in October 2011. Baumeister and Hamilton (2019) reproduced the methodology by which the original index was constructed to extend the series up to July 2018.3 The bottom panel of Figure 2 plots the cyclical component of the log of this series, again using the two-year difference. Unlike Kilian’s indexes, the industrial production data imply that the 1974-75 and 2008-2009 recessions were clearly the most significant downturns in global real activity during this period. And the December value of this series turns out to have an R2 of 77% for explaining annual world real GP growth.
Kilian and Zhou (2018) argued that another benefit of using real shipping costs is that whereas world industrial production describes the current month, real shipping costs should be forward-looking, and thus may be better predictors of future economic activity. To investigate this, I repeated the regressions using a monthly measure based on June rather than December of year τ. World industrial production continues to do well by this measure. Interestingly, the Kilian indexes actually have the wrong sign.
Kilian and Zhou (2018) further suggested that shipping costs may be more closely related to commodity prices than other measures. Hamilton (2019) investigated this claim using a number of different commodity prices, regressing the monthly change in the log of a particular commodity price on 3 of its own lags and 3 lags of a proposed measure of world economic activity. The commodity prices I looked at are the World Bank’s two broad commodity price indexes (energy and non-energy), two more specialised indexes (agriculture and base metals), and prices of four important individual commodities (crude oil, soybeans, aluminium and copper). Industrial production is a statistically significant predictor of every commodity except aluminium. By contrast, the Kilian-Zhou index does not give statistically significant predictions of any of these prices. The Kilian (2019) index gives better forecasts than Kilian-Zhou (2018) and is statistically significant for purposes of predicting the agricultural price index, the base-metals price index, and copper prices. But it is never as good as industrial production.
I conclude that although shipping costs offer a plausible option for measuring the level of real economic activity, in practice they do not work nearly as well as estimates of global industrial production, particularly after 2015. If one wanted to use real shipping costs, the two-year change in the natural log of real shipping costs is a better measure than residuals from a regression on a linear time trend.
I close by noting that one appealing feature of shipping costs is that a measure like the Baltic Dry Index is actually available daily.4 I show how one can use this daily series along with the monthly CPI to construct a daily measure of the cyclical component of real shipping costs, calculated using the two-year difference approach in the second panel of Figure 2 (Hamilton 2019).5 This measure is plotted in Figure 3 and might be used for applications where a daily rather than a monthly indicator is needed.
Figure 3 Daily cyclical component of real shipping cost (16 March 2011 to 16 July 2018)
Source: Hamilton (2019).
References
Antolín-Díaz, J, and J F Rubio-Ramírez (2018). “Narrative sign restrictions for SVARs”, American Economic Review 108(10): 2802-2829.
Anzuini, A, P Pagano and M Pisani (2015). “Macroeconomic effects of precautionary demand for oil”, Journal of Applied Econometrics 30: 968-986.
Baumeister, C, and J D Hamilton (2019). “Structural interpretation of vector autoregressions with incomplete identification: Revisiting the role of oil supply and demand shocks”, American Economic Review 109(5).
Baumeister, C, and G Peersman (2013). “The role of time-varying price elasticities in accounting for volatility changes in the crude oil market”, Journal of Applied Econometrics 28: 1087-1109.
Bruno, V G, B Büyükşahin and M A Robe (2016). “The financialization of food?”, American Journal of Agricultural Economics 99: 243-264.
Charnavoki, V, and J J Dolado (2014). “The effects of global shocks on small commodity-exporting economies: Lessons from Canada”, American Economic Journal: Macroeconomics 6: 2017-2037.
Degiannakis, S, G Filis and R Kizys (2014). “The effects of oil price shocks on stock market volatility: Evidence from European data”, Energy Journal, 35: 35-56.
ElFayoumi, K (2018). “The balance sheet effects of oil market shocks: An industry level analysis”, Journal of Banking and Finance 95: 112-127.
Gargano, A, and A Timmermann (2014). “Forecasting commodity price indexes using macroeconomic and financial predictors”, International Journal of Forecasting 30: 825-884.
Hamilton, J D (1994). Time series analysis, Princeton University Press.
Hamilton, J D (2018). “Why you should never use the Hodrick-Prescott Filter”, Review of Economics and Statistics 100: 831-843.
Hamilton, J D (2019). “Measuring global economic activity”, working paper, UCSD.
Herwartz, H, and M Plödt (2016). “The macroeconomic effects of oil price shocks: Evidence from a statistical identification approach”, Journal of International Money and Finance 61: 30-44.
Juvenal, L, and I Petrella (2014). “Speculation in the oil market”, Journal of Applied Econometrics 30: 621-649.
Kang, W, F Perez de Gracia and R A Ratti (2017). “Oil price shocks, policy uncertainty, and stock returns of oil and gas corporations”, Journal of International Money and Finance, 70: Pages 344-359.
Kilian, L (2009). “Not all oil price shocks are alike: Disentangling demand and supply shocks in the crude oil market”, American Economic Review 99: 1053-1069.
Kilian, L (2019). “Measuring global real economic activity: Do recent critiques hold up to scrutiny?”, Economic Letters 178: 106-110.
Kilian, L, and D P Murphy (2014). “The role of inventories and speculative trading in the global market for crude oil”, Journal of Applied Econometrics 29: 454-478.
Kilian, L, and X Zhou (2018). “Modeling fluctuations in the global demand for commodities”, Journal of International Money and Finance 88: 54-78.
Knotek, E S, and S Zaman (2017). “Nowcasting US headline and core inflation”, Journal of Money, Credit and Banking 49: 931-968.
Kwiatkowski, D, P C B Phillips, P Schmidt and Y Shin (1992). “Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root?”, Journal of Econometrics 54(1-3): 159-178.
Lütkepohl, H, and A Netšunajev (2014). “disentangling demand and supply shocks in the crude oil market: How to check sign restrictions in structural VARs”, Journal of Applied Econometrics 29: 479-496.
McPhail, L L (2011). “Assessing the impact of US ethanol on fossil fuel markets: A structural VAR approach”, Energy Economics 33: 1177-1185.
Odom, P (2010). “Shipping indexes signal global economic trends”, in Annual Report, Globalization and Monetary Policy Institute 2010: 28-35.
Wieland, J (forthcoming). “Are negative supply shocks expansionary at the zero lower bound?”, Journal of Political Economy.
Endnotes
[1] See McPhail (2011), Baumeister and Peersman (2013), Charnavoki and Dolado (2014), Degiannakis et al. (2014), Gargano and Timmermann (2014), Juvenal and Petrella (2014), Kilian and Murphy (2014), Lütkepohl and Netšunajev (2014), Anzuini et al. (2015), Herwartz and Plödt (2016), Kang et al. (2017), Antolín-Díaz and Rubio-Ramírez (2018), ElFayoumi (2018), Kilian and Zhou (2018), and Wieland (forthcoming), among many others.
[2] Performing these tests requires the level of the original series, which Kilian has never reported. However, I show in my paper (Hamilton 2019) that it is possible to reconstruct the original series from the regression residuals that were published by Kilian and post the levels of the underlying nominal and real indexes at http://econweb.ucsd.edu/~jhamilton/REA.zip.
[3] This series is regularly updated at https://sites.google.com/site/cjsbaumeister/research.
[4] Daily values for the BDI were obtained from TradingEconomics.com. Kilian has used the monthly log growth of the BDI rather than an average of individual shipping cost growth rates to update his series since 2008.
[5] Bruno et al. (2016) use residuals from a regression of the BDI on a linear time trend to construct a weekly indicator of economic activity. They do not propose solutions on how to develop this into a practical real-time estimator.