Everyday life involves repeated interactions among very different individuals who need to cooperate to achieve mutually advantageous outcomes. Economists, along with other social scientists, have emphasised the role of psychological and institutional mechanisms in such interactions (Fehr and Gächter 2000, Enke 2017a, 2017b). However, in situations where interactions are repeated, cooperation can be overly complex. Individuals will often renege on cooperation, either due to involuntary mistakes or deliberately. Thus, understanding when and how to retaliate or forgive efficiently is not straightforward.
Accordingly, in earlier work (Proto et al. 2018, 2019), we show that when subjects are allocated into two groups according to their cognitive skills, only the groups with higher cognitive skills converge to full cooperation in complex, non-zero-sum games such as the repeated Prisoner's Dilemma.1 However, such a separation of individuals into distinct classes of cognitive skills seldom occurs in everyday life. The experimental economics literature has shown that when people are not separated according to their cognitive skills, if gains from cooperation are sufficiently large, they tend to choose efficient strategies leading to cooperation under repeated interactions (e.g. Blonski et al. 2011, Dal Bó 2005, Dal Bó and Fréchette 2011, Dreber et al. 2008, Duffy and Ochs 2009). The questions of how groups interact and how people of diverse types within groups influence one another remain open.
Our research (Proto et al. forthcoming) offers several insights to answer these open questions. In a standard, indefinitely repeated Prisoner’s Dilemma game, cooperation rates in heterogeneous groups are closer to the higher cooperation rate that is observed in groups composed exclusively of individuals with high cognitive skills.
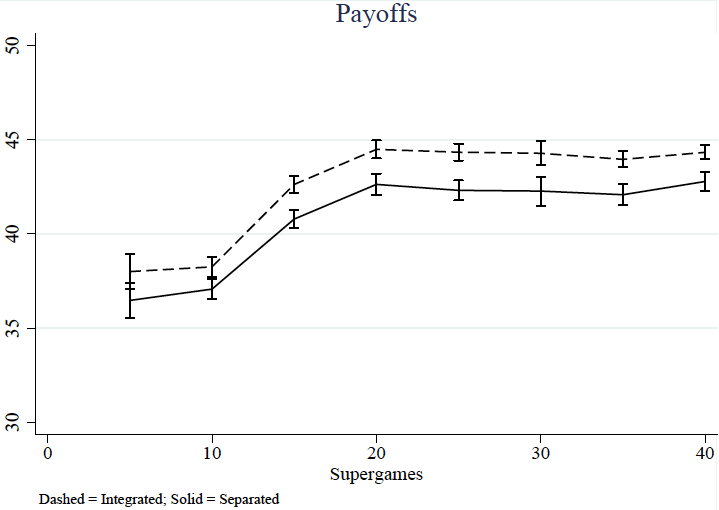
Figure 1 Aggregate payoffs in the indefinitely repeated prisoner’s dilemma in the two treatments
Notes: In the integrated treatment players of heterogeneous cognitive abilities are pooled together. In the separated treatment, players are allocated in different groups according to their cognitive skills as measured by the Raven test.
This higher cooperation rate results in aggregate payoffs being higher when players of heterogeneous ability are integrated and play together than when they play separately (Figure 1). Interacting in integrated groups is more beneficial for players of lower cognitive skill compared with when they interact separately, while players of higher cognitive skill are on average worse off.
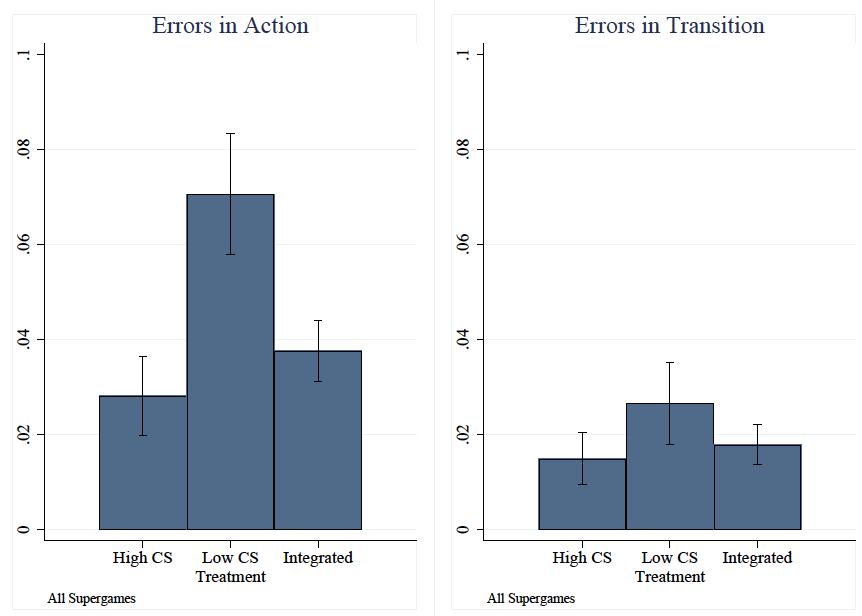
Furthermore, we find that the higher cooperation rate of players with lower cognitive skill levels in integrated groups is due to the influence of the more skilled players. Higher cognitive ability players are more consistent in their strategy implementation. In Figure 2, we present the average errors in strategy implementation by the different groups of players. Players in the integrated session commit less mistakes than in the low cognitive skills session. In the paper we also show that players with low skills in separated groups commit more mistakes than players of the same skills in integrated groups.
Figure 2 Errors in strategy implementation for players with different cognitive skill levels in the indefinitely repeated prisoner’s dilemma
Notes: Errors in action are simple ‘trembling hand’-type errors. Errors in transition are errors in correctly implementing a strategy given the history of play due to limitations in working memory. High CS and Low CS are the high and low cognitive skill groups in the separated treatment respectively and Integrated are the integrated groups.
Our experimental data show that players learn to cooperate with experience. The choice of strategy depends not only on their own cognitive skills but also on the distribution of cognitive skills in the group they interact with. High cognitive ability players are more lenient when they play separately with other high cognitive ability players than when they play in integrated groups. We analyse this complex mechanism using a model of evolutionary game theory.
We study the effect of varying levels of error rates on the frequency of strategies in the population in evolutionary equilibria of two models: the proportional imitation model (Schlag 1998) and the best response model (Gilboa and Matsui 1991). We assume that players choose one of the following three strategies: Always Defect, Tit-for-Tat (cooperate if partner cooperated in the previous period, otherwise defect), and Grim Trigger (cooperate if both players cooperate and never cooperate again after any deviation). This assumption relies on established findings in experimental studies of the repeated Prisoner's Dilemma game, which are replicated in our data.
Figure 3 describes the dynamics in the best response model (similar dynamics arise in the proportional imitation model). The size of the basin of attraction gives us a measure of the probability that each of the three strategies will be prevalent near to the steady-state equilibrium. The size of these basins changes with the probability of errors. In each of the panels of Figure 3, the triangular area is split into three sub-regions. Each of these represents the basin of attraction of the strategy contained in the boundary of each sub-region. For example, across all four panels, the bottom left triangle is the basin of attraction for the Always Defect strategy. As players become more error prone, the basin of attraction of harsher strategies becomes larger. That is, the size of the basin of attraction of Always Defect becomes larger than that of both Grim Trigger and Tit-for-Tat, and that of Grim Trigger becomes larger than that of Tit-for-Tat.
Figure 3 Basin of attraction of the three strategies
Notes: The basins of attractions can be interpreted as the likelihood of converging to one of the three strategies considered in the model: ‘Grim Trigger’, ‘Tit-for-Tat’ and ‘Always Defect’.
Our experimental data corroborate our theoretical analysis. The frequency of errors is inversely related to the proportion of high cognitive ability players in a group. With fewer high cognitive ability players, we find that the frequency of errors increases and as a result we find harsher strategies being implemented.
Despite the many forces in society that tend to segregate individuals according to similar characteristics, a large part of social interaction occurs among individuals who are very different from one another in many respects. Our study highlights how cognitive ability is one especially important characteristic. Further research on cooperation rates among individuals with different characteristics can be illuminating and can help provide useful tools for policy.
Our results may provide useful guidance for policies affecting social interaction among individuals that are heterogeneous in education levels (which generally positively correlate with cognitive skills), such as the interactions fostered by ‘moving to opportunity’ (MTO) policies.2 We show that integration can be surplus-enhancing in principle, but social interactions are likely to be mediated by differences in cognitive skills, which are likely to occur as consequences of these policies.
References
Blonski, M, P Ockenfels and G Spagnolo (2011), “Equilibrium selection in the repeated prisoner's dilemma: Axiomatic approach and experimental evidence”, American Economic Journal: Microeconomics 3(3): 164-192.
Dal Bó, P (2005), “Cooperation under the shadow of the future: Experimental evidence from infinitely repeated games”, American Economic Review 95(5): 1591-1604.
Dal Bó, P and G R Fréchette (2011), “The evolution of cooperation in infinitely repeated games: Experimental evidence”, American Economic Review 101(1): 411-429.
Dreber, A, D G Rand, D Fudenberg and M A Nowak (2008), “Winners do not punish”, Nature 452: 348-351
Duffy, J and J Ochs (2009), “Cooperative behavior and the frequency of social interaction”, Games and Economic Behavior 66(2): 785-812.
Enke, B (2017a), “Kinship systems, cooperation and the evolution of culture”, National Bureau of Economic Research.
Enke, B (2017b), “The coevolution of kinship systems, cooperation, and culture”, VoxEU.org, 21 September.
Fehr, E and S Gächter (2000), “Cooperation and punishment in public goods experiments”, American Economic Review 90(4): 980-994.
Gilboa, I and A Matsui (1991), “Social stability and equilibrium”, Econometrica 59(3): 859-67.
Plomin, R and I J Deary (2015), “Genetics and intelligence differences: five special findings”, Molecular Psychiatry 20(1): 98-108.
Proto, E, A Rustichini and A Sofianos (2018), “Why societies cooperate”, VoxEU.org, 19 January.
Proto, E, A Rustichini and A Sofianos (2019), “Intelligence, personality, and gains from cooperation in repeated interactions”, Journal of Political Economy 127(3): 1351-1390.
Proto, E, A Rustichini and A Sofianos (forthcoming), “Intelligence, Errors and Cooperation in Repeated Interactions”, Review of Economic Studies.
Schlag, K (1998), “Why imitate, and if so, how? a boundedly rational approach to multi-armed Bandits”, Journal of Economic Theory 78(1): 130-156.
Endnotes
1 The cognitive skills are measured using advanced progressive Raven matrices, as is common in the literature.
2 Cognitive skills are found to depend on various factors. Environment, education, and socio-economic status are as relevant in determining cognitive skills as genetic characteristics. See, for example, Plomin and Deary (2015).