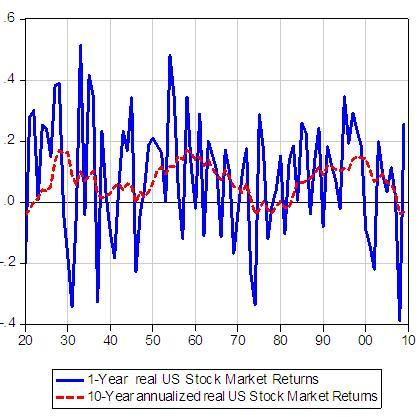
Figure 1 shows 1-year and 20-year annualised US stock market returns (S&P500 index) over the course of nearly the last century. Returns are determined by a “slow-moving” information component and by a “noise” component. The noise component dominates the data at high frequencies, while the information component emerges when high-frequency observations are aggregated over time to construct long-horizon returns.
Figure 1
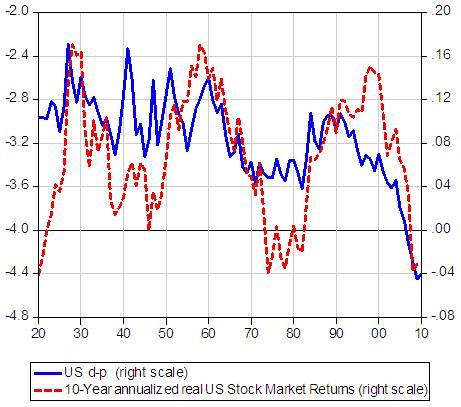
As the information component is naturally related to “fundamentals”, Figure 1 helps understand the empirical evidence that fundamentals perform better in predicting returns as the predictive horizon gets longer. In particular, the dynamic dividend growth model (Campbell-Shiller 1988) suggests that the relevant fundamental to capture the information component in stock market returns is the dividend-price ratio. This variable regularly plays an important role in recent empirical literature that has replaced the long tradition of the efficient market hypothesis with a view of predictability of returns (see for example, Cochrane 2007). But there is an ongoing debate on the robustness of return predictability and its potential use from a portfolio allocation perspective (Boudoukh et al. 2008). The essence of this debate is captured by Figure 2 that reports the US dividend/price ratio along with the 20-Year annualised stock market returns.
Figure 2
The Figure shows the presence of some co-movement between the two variables. This is somewhat limited by the fact that the dividend-price shows a very high degree of persistence that does match the mean reversion of the returns. This high degree of persistence contradicts one of the crucial hypotheses of the dynamic dividend growth model that is based on the assumption that the dividend-price is a stationary variable. This degree of persistence is at the heart of the debate on the robustness of the statistical evidence on the predictability of stock market returns.
Is there a role for demographics?
Intuitive reasoning hints at demography as an important variable to determine the long-run behaviour of the stock market, while it is difficult to imagine a relationship between high-frequency fluctuations in stock market prices and a slow-moving trend determined by demographic factors.
In fact, a theoretical model by Geanakopoulos et al. (2004) predicts that a specific demographic variable – the ratio of middle-aged to young population – explains fluctuations in the dividend yield.
Geanakopoulos and his co-authors consider an overlapping generation model in which the demographic structure mimics the pattern of live births in the US, that have featured alternating twenty-year periods of boom and busts. They conjecture that the life-cycle portfolio behaviour – which suggests that agents should borrow when young, invest for retirement when middle-aged, and live off their investment once they are retired – plays an important role in determining equilibrium asset prices. Consumption smoothing by the agents, given the assumed demographic structure, requires that when the middle-aged to young population ratio is small, there will be excess demand for consumption by a large cohort of retirees and for the market to clear, equilibrium prices of financial assets should adjust, i.e. decrease. The result is that saving is encouraged for the middle-aged. As the dividend/price ratio is negatively related to fluctuations in prices, he model predicts a negative relation between this variable and the middle-aged-to-young ratio.
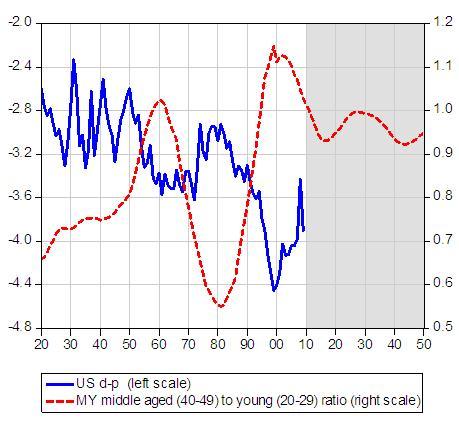
In a recent CEPR Discussion Paper (Favero et al. 2010), we take the Geanakopoulos et al. model to the data via the conjecture that fluctuations in the middle-aged-to-young ratio could capture a slowly evolving mean in the dividend price ratio within the dynamic dividend growth model. We find strong evidence in favour of using this variable together with the dividend/price ratio in long-run forecasting regressions for stock market returns, as Figure 3 and Figure 4 illustrate.
Figure 3
Figure 3 reports the dividend price ratio and the middle-aged-to-young ratio to show how, in line with the predictions of Geanakopoulos et al., a negative relation between the middle-aged-to-young ratio and the dividend price is present in the data. The demographic variable captures the slowly evolving information component in the fundamental. Does this help to predict long-horizon stock market returns? Yes. In fact, the econometric based yes, contained in our CEPR paper, is visually illustrated by Figure 4, which reports the middle-aged-to-young ratio, 10-year stock market returns, and the deviation of the dividend-price ratio from its slowly time varying mean captured by the middle-aged-to-young ratio.
Figure 4

Figure 4 also illustrates an additional interesting feature of the middle-aged-to-young ratio. Long-run forecasts for this (exogenous) variable are readily available. In fact, the Bureau of Census provides projections up to 2050 for the middle-aged-to-young ratio. In our paper we exploit the exogeneity and the predictability of the demographic ratio to project the equity risk premia up to 2050. Our simulations point to an average equity risk premium of about 5% for the next forty years.
The research agenda
The empirical evidence of a stable relation between a demographic variable and long-horizon US stock market returns naturally generates a number of interesting research questions.
- First, the fact that a slow moving variable determined by demographics has very little impact on predictability of stock market returns at high frequency but a sizeable and strongly significant impact at low frequency has some obvious consequences on the slope of stock market risk, defined as the conditional variance and covariance per period of asset returns. Demographics should then become a natural input into the optimal asset allocation decision of a long-horizon investor.
- Second, what about the bond market? If the middle-aged-to-young ratio plays an important role in capturing an information component that helps to predict long-horizon stock market returns it should also have a role in capturing a persistence components also in bond-yields.
- Third, what is the international evidence? Our empirical results are so far limited to the US case only, but it is important to assess their robustness when the model is extended to other countries.
References
Boudoukh, Jacob, Mathew Richardson, and Robert F Whitelaw (2008), “The Myth of Long-Horizon Predictability”, The Review of Financial Studies, 21(4):1577-1605.
Campbell, John Y and Robert Shiller (1988), “Stock Prices, Earnings, and Expected Dividends”, Journal of Finance, 43:661-676.
Cochrane, John H (2007),”The Dog that Did Not Bark: A Defence of Return Predictability”, Review of Financial Studies, 20, 5.
Favero, Carlo A, Arie E Gozluklu and Andrea Tamoni (2009) “Demographic Trends, the Dividend-Price Ratio and the Predictability of Long-Run Stock Market Returns” , CEPR working paper 7734, forthcoming in the Journal of Financial and Quantitative Analysis.
Geanakoplos, John, Michael Magill and Martine Quinzii (2004), “Demography and the Long Run Behaviour of the Stock Market”, Brookings Papers on Economic Activities, 1: 241-325.