In an interesting empirical analysis, Drechsler et al. (2017) (henceforth, DSS) study the effects of changes in the policy rate on the amount of bank deposits in local markets depending on the degree of market power in these local markets. In particular, in a panel regression they show that increases in the Federal funds rate lead to negative changes in deposits at bank branches located in concentrated counties relative to those in less concentrated counties. This result is then used to propose a novel explanation of the effect of monetary policy on bank lending, called the ‘deposits channel’ of monetary policy. In the words of DSS: “When the Fed funds rate rises, banks widen the interest spreads they charge on deposits, and deposits flow out of the banking system. Since banks rely heavily on deposits for their funding, these outflows induce a contraction in lending.” The authors also present a theoretical model of imperfect competition in a local banking market which can account for their empirical findings.
In a recent paper (Repullo 2020), I present a critical review of DSS's theoretical model, showing that increases in the policy rate have ambiguous effects on the equilibrium amount of deposits. In particular, the relationship is U-shaped – first decreasing and then increasing. Since their model does not yield simple analytical solutions, I construct an alternative model of imperfect competition in a local banking market, based on a simple microfoundation for the households' demand for deposits, which is consistent with their panel results but contradicts their conclusion. In this model, increases in the policy rate always increase the equilibrium amount of deposits.
DSS’s theoretical model
DSS's model features a representative household with an initial amount of wealth that can be invested in three types of assets: cash that pays a zero interest rate, deposits of a set of n banks that pay the equilibrium deposit rate, and market assets (bonds) that pay the policy rate set by the central bank. The demand for bank deposits is derived from a utility function that depends on final wealth and liquidity services provided by cash and deposits. Banks offer differentiated deposits and compete à la Bertrand by setting deposit rates, or equivalently spreads between the policy rate and the deposit rate. Equilibrium spreads are derived from the symmetric Nash equilibrium of the game played by the banks. Using this framework, DSS then study the effect of an exogenous change in the policy rate on equilibrium spreads and deposits.
The model is fairly complicated, and DSS derive results for the limit case in which the weight of liquidity services in the household's utility function goes to zero. My approach to the analysis of this model is to start with the simple case of a monopoly bank. In this case, I show that increases in the policy rate increase equilibrium spreads, but have an ambiguous effect on equilibrium deposits: the relationship has a negative slope (as claimed by DSS) for low rates and a positive slope for high rates (contrary to their claim).
To understand the reason behind these results, it is convenient to consider a model without cash in which the household’s choice is limited to the allocation of her initial wealth between bonds and deposits at the monopoly bank. In such a model, the effect of an increase in the policy rate on equilibrium deposits can be decomposed into a negative substitution effect, due to increase in the spread by the monopoly bank, and a positive income effect, due to higher return to the household's initial wealth. Moreover, this decomposition helps to understand why an increase in the policy rate may lead to an increase in the equilibrium amount of deposits in the model with cash as the income effect increases the household's demand for liquid assets (both cash and deposits).
The results for the model without cash are also helpful in understanding why the equilibrium quantity of deposits is initially decreasing in the policy rate. In this model, when the policy rate tends to zero, deposits yield the same return as bonds, but in addition they provide valuable liquidity services. So we get a corner solution in which the household invests all her wealth in deposits. Increases in the policy rate eventually lead the household to move away from the corner, decreasing her investment in deposits. But at some point the power of the income effect kicks in, leading to the upward sloping relationship noted above.
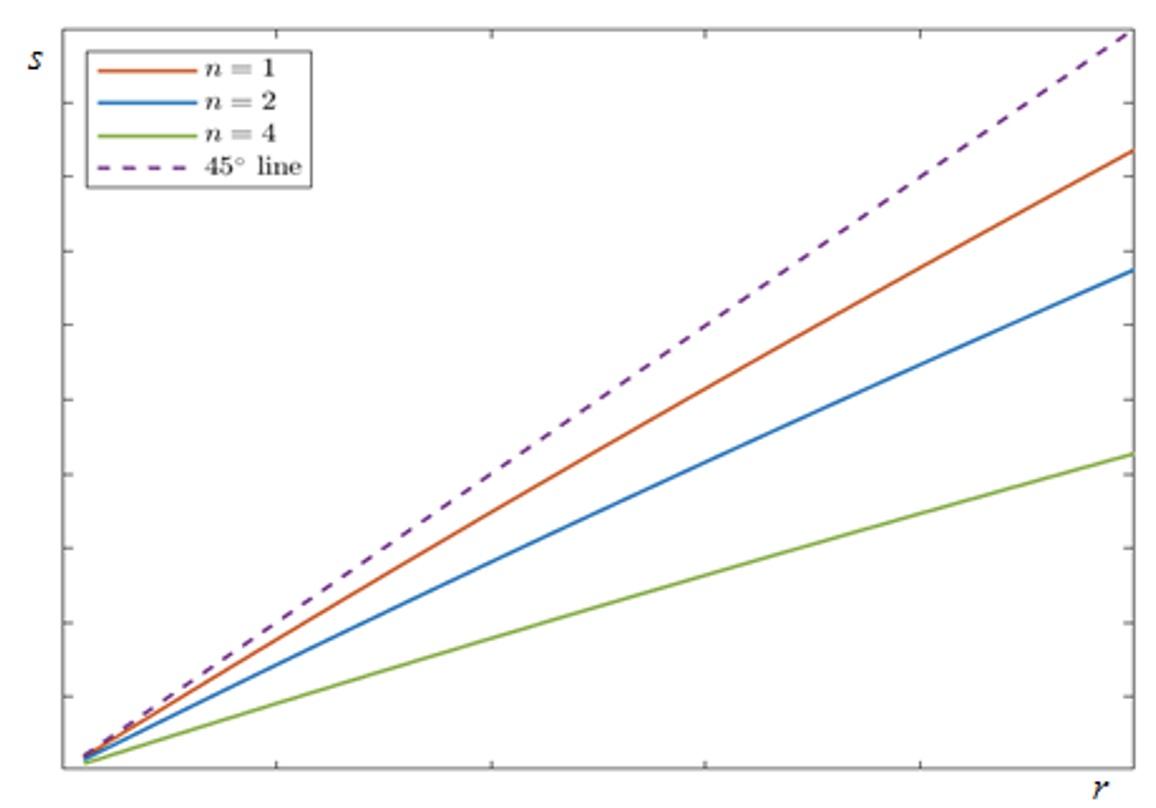
Next, I consider the general oligopoly model with n banks, for which I obtain the results summarized in the following figures. Figure 1 shows the relationship between the equilibrium spread s, defined as the difference between the policy rate r and the equilibrium deposit rate rD, and the policy rate r for three values of the number of banks n, namely n = 1, n = 2, and n = 4. The results show that the equilibrium spread s is increasing in the policy rate r and decreasing in the number of banks n. Thus, higher competition leads to lower spreads for any value of the policy rate.
Figure 1 Equilibrium spreads
The slope of the relationship between equilibrium spread s and the policy rate r is what DDS call the spread beta. In line with their empirical findings, the spread beta is decreasing in the number of banks n. In other words, the positive effect of the policy rate r on the equilibrium deposit rate rD is smaller in concentrated markets.
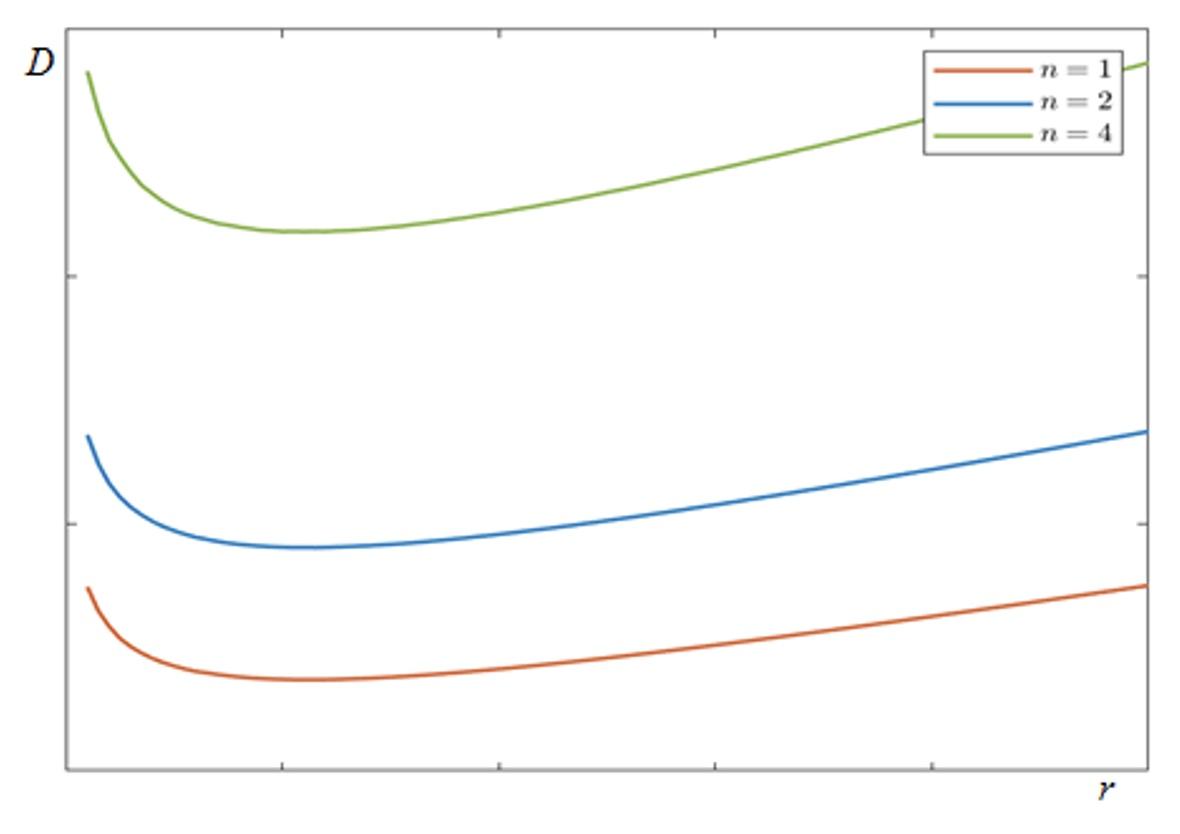
Figure 2 shows the relationship between the equilibrium amount of deposits D and the policy rate r for three values of the number of banks n, n = 1, n = 2, and n = 4. The results show that the equilibrium amount of deposits D is first decreasing and then increasing in the policy rate r. Moreover, the effect of competition on spreads implies that higher competition leads to higher deposits.
Figure 2 Equilibrium deposits
It should be noted that, due to the complexity of the model, the previous results essentially rely on numerical solutions. To verify the robustness of the results, I construct a simple model of Cournot competition in a local banking market for which analytical results can be derived.
An alternative model
The alternative model features a large set of heterogeneous households that differ in a utility premium associated with liquid assets. As in DSS, households have an initial wealth that can be invested in three types of assets: cash that pays a zero interest rate, deposits of a set of n banks that pay the equilibrium deposit rate, and market assets (bonds) that pay the policy rate set by the central bank. Assuming that cash provides higher liquidity services than deposits, it turns out that households with a high liquidity premium invest all their wealth in cash, households with an intermediate liquidity premium invest all their wealth in deposits, and households with an low liquidity premium invest all their wealth in bonds.
From here I derive a linear demand for deposits, that is increasing in the deposit rate rD and decreasing in the policy rate r, and compute the corresponding symmetric Cournot equilibrium for a market with n banks. The equilibrium has two interesting properties. The first one is that, in contrast with DSS’s claim, an increase in the policy rate r always increases the equilibrium amount of deposits D. The second one is that, in line with DSS’s panel results, the positive effect of the policy rate r on equilibrium deposits D is weaker when banks have high market power (low n).
Conclusion
Drechsler et al. (2017) claim that the transmission of monetary policy should be understood from the liability side of banks' balance sheets. In particular, they argue that there is a ‘deposits channel’ through which increases in the policy rate widen deposit rate spreads, leading to deposit outflows that reduce banks’ lending capacity. In Repullo (2020), I show that, contrary to their claim, in their theoretical model of imperfect competition in a local banking market, increases in the policy rate have ambiguous effects on the equilibrium amount of deposits. I have also constructed an alternative model, based on a simple microfoundation for the households' demand for deposits, which is consistent with their panel results and where increases in the policy rate always increase the equilibrium amount of deposits.
I would like to conclude with a comment on DSS's approach. They look at the effect of monetary policy on bank lending through the lens of deposit taking. In this approach, the characteristics of the loan market take a back seat. While it is true that “deposits are a special source of funding for banks, one that it is not perfectly substitutable with wholesale funding.”, it is also true that if the focus of the analysis is on bank lending, characteristics such as market power and risk-taking in lending should have a prominent role. For this reason, one should aim at building models that encompass both sides of banks' balance sheets.
References
Drechsler, I, A Savov and P Schnabl (2017), “The Deposits Channel of Monetary Policy,” Quarterly Journal of Economics 132: 1819-1876.
Repullo, R (2020), “The Deposits Channel of Monetary Policy: A Critical Review,” CEPR Discussion Paper No. 15553.