Search models have been instrumental in understanding market phenomena that are hard to reconcile in classical economic theory, such as the coexistence of unemployment and vacancies, price or wage dispersion and stickiness, bid-ask spreads, the difficulties of bilateral trade that generate a role for money and related institutions, partnership formation, and long and variable durations in the time to execute trades in labour, housing, and other markets. Models in the celebrated Diamond-Mortensen-Pissarides tradition of random search provide a unifying explanation for many of these facts. Yet in their endeavour they tend to strip away a key guiding force from classical models, namely, the price. In particular, they tend to treat price formation as an afterthought that has to be sorted out once agents meet (usually through bargaining) but that cannot be used to guide individuals’ search decisions. Since the price does not guide the meeting process, efficiency is not obtained except under very special conditions.
What would be an alternative way to think about the effect of prices and wages in shaping the way agents search for trading partners? The fast-growing literature on ‘directed search’ aims to keep the explanatory power of search models, but allows for a meaningful role of prices in determining where people search for a trading partner. For example, in the labour market a higher wage is assumed to attract more applicants on average, and decreases the time a firm needs to fill its vacancy, but in contrast to classical models it does not reduce it to zero. Rather, more generous offers are linked to a higher probability of trading, so they price the waiting time. Because of the importance of prices these models are often also called competitive search models. This literature has its origins in simple IO models as in Peters (1984, 1991) and Burdett et al. (2001) and macro models as in Moen (1997) and Acemoglu and Shimer (1999), but has reached out to many branches of micro and macro including diverse topics such as competitive posting of auctions, on-the-job search, or monetary theory and trade in asset markets. The aim of our survey in Wright et al.(2017) is to review, consolidate, and extend the literature on this topic.
Competitive search bundles two characteristics: the terms of trade are posted by agents in advance of meetings, and these terms direct search and hence help determine who meets whom. Relative to random search, this is not only a different philosophical approach to the study of markets, but the combination of posting and directed search also alters substantive findings. In particular, posted prices give agents incentives to seek out particular counterparties. This often leads to market efficiency (it is sometimes said the models internalise search externalities). Moreover, they dispense with the usual need for an additional parameter that determines the bargaining weights of the two sides of the market – the level of transfers is chosen strategically in the model to balance the costs with the benefits of quicker and/or better matches. Some of the models, but not all, avoid the need for assuming a matching function because of the micro-foundations of the actual search behaviour. Finally, the theory is tractable, often delivers cleaner results than alternatives, and bridges gaps between traditional search, general equilibrium, and game theory.
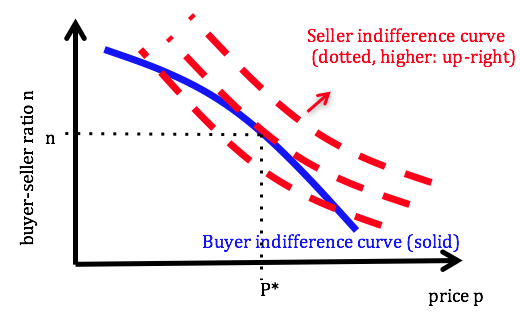
As a stylised preview of the main mechanism that underlies these models, consider the simplest setting with homogeneous buyers and sellers (in the labour market analogue firms are the buyers of labour and workers are the sellers). If trade occurs at price p, buyers obtain a utility of 1 minus the price p, and buyers obtain utility p. No trade leads to zero utility. At different prices, different queues n(p) of buyers and sellers arise. A matching function determines the probability α that seller trades with a buyer, which is increasing in the buyer-seller ratio n(p) that is formed at price p. So, their expected utility is α times p. Since α is increasing in the buyer-seller ratio, this can be represented as indifference curves over (p,n) pairs, as shown in Figure 1, where the benefits of longer queues of buyers are offset by higher prices. Higher utility is associated with higher curves. If a seller offers a higher price he changes the queue length and affects the probability of trade.
Figure 1 Indifference curves over (p,n)
How much does he affect the queue? Buyers’ expected utility consists of the gains from trade 1-p times their trading probability, which is decreasing in the queue of other buyers n. In equilibrium this expected utility takes some value U, which can be viewed as an indifference curve over (p,n) pairs for the buyer. Figure 1 illustrates such an indifference curve, where higher prices are compensated for by shorter queues for the good. Sellers choose a price-queue pair on this curve to bring them to their highest indifferent curve, yielding equilibrium point (p*,n*). This Edgware-Box representation highlights the competitive part of these search models – agents care about two margins (price and trading probability), and the prices aim to balance not just the purchase of the goods but also the trading probabilities. The market reaches a point of efficiency despite the trading frictions. For this outcome, it does not matter which side posts the price as long as the matching function remains unchanged.
Our survey reviews the theory more generally, with examples both in static economies as well as with repeat purchases in labour, housing, or goods markets and in monetary economics. It aims to provide enough of the mathematical setup to allow novices an entrance into this growing literature, while providing depth and a broad review for those who are already somewhat familiar. It also reviews the micro-foundations that underlie the insights just described in the form of finite games, shows how to handle heterogeneity and larger contracts spaces beyond simply posting prices, presents existing evidence about the directedness of search, and keeps an eye on economic applications.
References
Acemoglu, D, and R Shimer (1999), “Holdups and Efficiency with Search Frictions,” International Economic Review, 40, 827-850.
Burdett, K, S Shi and R Wright (2001), “Pricing and Matching with Frictions,” Journal of Political Economy 109, 1060-1085.
Moen, E R (1997), “Competitive Search Equilibrium,” Journal of Political Economy 105, 385-411.
Peters, M (1984), “Bertrand Equilibrium with Capacity Constraints and Restricted Mobility,” Econometrica 52, 1117-1128.
Peters, M (1991) “Ex Ante Price Offers in Matching Games: Non-Steady States,” Econometrica 59, 1425-1454.
Wright, R, P Kircher, B Julien and V Guerrieri (2017), “Directed Search – A Guided Tour”, NBER working paper 23884.