With the Eurozone in recovery, at some stage the ECB will tighten monetary conditions.1 It will naturally start that process by tapering its bond purchases. But at some later stage it will also raise interest rates. Under what economic conditions might it do so? In this column, I try to shed some light on that issue by looking at the ECB’s past interest rate setting behaviour.
I draw two main conclusions. First, the ECB responds strongly to changes in the state of the business cycle and, in particular, to the outlook for prices. While the statistical analysis suggests that the likelihood of an interest rate increase currently is about 7%, a combination of stronger growth and higher price pressures could quickly raise that probability to about 30%. (Past interest rate increases by the ECB have on average been associated with the model predicting a 30% probability of an increase.)
Second, following the onset of the financial crisis in 2008, the ECB’s interest rate setting behaviour changed as it became less likely to raise interest rates and more likely to cut them, given economic conditions. The reason for this shift was most likely that the monetary transmission mechanism had become dysfunctional. Had the ECB’s behaviour not changed, the likelihood of an interest rate increase would now be about 30%. Thus, a return of the ECB to its pre-crisis behaviour would lead to a dramatic rise in the likelihood of an interest rate increase.
Modelling central bank interest rate setting
A large body of analysis shows that the main factors impacting central banks’ interest rate decisions are inflation and the state of the business cycle. The business cycle matters either because, as the Phillips curve suggests, it is a determinant of inflation, or because stabilising the economy around its growth path is an independent goal of monetary policy.
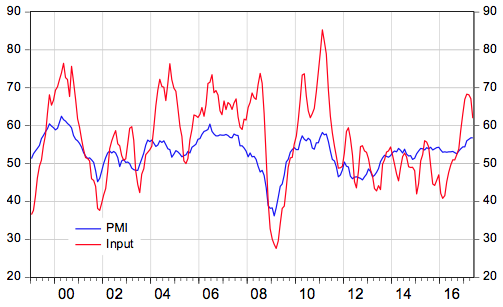
The analysis uses the Eurozone Purchasing Managers Index (PMI), which is a good indicator of real GDP growth over four quarters, to capture the ECB’s assessment of the state of the business cycle. Furthermore, it uses the PMI for manufacturing input prices, which contains information useful for forecasting future Harmonised Index of Consumer Prices (HICP) inflation, to capture the ECB’s views of inflation pressures.
While these are soft indicators of economic conditions, they summarise the state of the economy better than hard data since they are available much more rapidly, are less sensitive to a host of data problems,2 and they are inherently forward-looking. They are therefore likely to be strongly correlated with the ECB’s views of economic conditions.
Figure 1 shows that the PMI captures the weakness of economic activity following the ‘dot.com’ bubble bursting in 2001, the collapse of Lehman in 2008, and the sovereign debt crisis that started in 2011. The PMI for input prices shows the rise in inflation pressures in 2008 and 2011. While both spikes were driven by oil prices, they led the ECB to tighten monetary policy. Interestingly, the high and positive correlation between the two series, 0.60, suggests that swings in the demand for goods and services were the main driver of the Eurozone economy over the period in question.
Figure 1 State of the business cycle and inflation in the Eurozone
A simple statistical model
To explore what information about ECB interest rate setting these variables contain, they are included in an econometric model3 of the ECB’s policy decision to cut, leave unchanged, or raise interest rates over the period February 1999 – June 2017. The model is estimated on data only for the months at which the Governing Council, the ECB’s decision-making body, met to set monetary policy.
The model includes the following variables:
- The lagged refinancing rate. If the interest rate reverts to some normal or average level, one would expect the ECB to be more likely to cut the interest rate, the higher it is. It enters the regression model with a negative sign and is borderline significant (p = 7.1%).4
- A variable capturing any change in the ECB’s interest rate setting from November 2008 onward. The parameter is negative and borderline significant (p = 7.3%). This indicates that, for any given set of economic conditions, the ECB has become less likely to raise interest rates, and more inclined to cut them.
- The (logarithms of the) PMI, input prices and their product. These are all highly significant (p = 0.2%, 0.1% and 0.1%). Increases in the PMI and input prices are thus the main determinants of the ECB’s decisions to change the interest rate.
A dummy variable taking the value of 1 from October 2008 onward to capture any changes in the ECB’s responses to the economy.
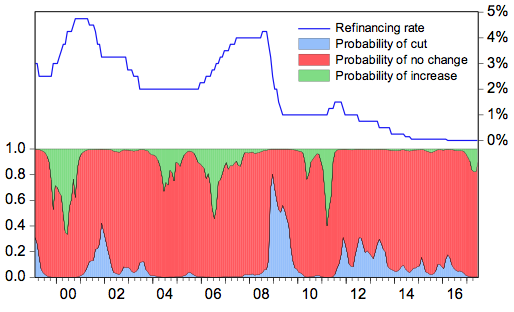
Figure 2 shows the ECB’s policy rate and the estimated probabilities of a cut in interest rates in light blue, of an increase in green of no change in red.
Figure 2 ECB policy rate and estimated probabilities of a change in interest rates
The probability of interest rate cuts is generally high when they are undertaken, and similarly for episodes of interest rate increases. But there are also some episodes when the model predicted policy changes and none happened. For instance, the model attached high probabilities to the ECB increasing interest rates in 2004, which it did not do.
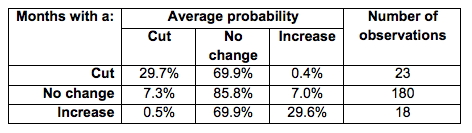
Table 1 provides more information about the model. The probability of an interest rate cut was, on average, 30% in the months when a cut was undertaken. Furthermore, the probability of an interest rate increase was, on average, 30% in the months an interest rate increase was undertaken.5 In months in which the ECB decided against changing interest rates, the model assigns a probability of 86% to that outcome, a probability of 7% to a cut, and the same probability to an increase.
Table 1 Estimated probabilities of interest rate changes in months with a cut, no change, and an increase, February 1999 – June 2017
Note: Percentages may not sum to unity because of rounding.
The current situation
Could the ECB decide to raise interest rates or, more likely, tighten monetary conditions now? That seems unlikely as the model attaches a probability of an interest rate increase in July 2017 (the last observation included in the study) of merely 7%.
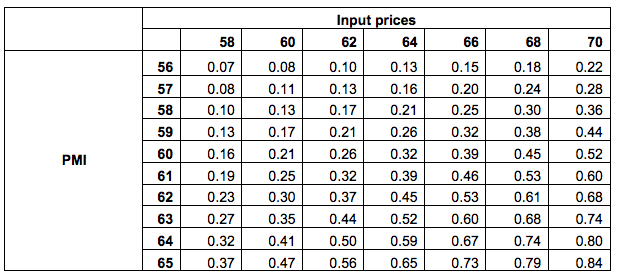
But if the economic conditions as captured by the PMI or input prices were to strengthen, an interest rate increase becomes more likely. To get a handle on this question, Table 2 shows the estimated probabilities for a set of hypothetical values of the PMI and input prices. To interpret the table, it is useful to recall that the PMI at the end of June 2017 was about 56 and the input price index about 58. (Moreover, it should be noted that these probabilities depend on the ECB’s refinancing rate which is currently zero.) Furthermore, recall that when the ECB increased interest rates, on average the model assigned a probability of about 30% to that outcome.
Table 2 Estimated probability of an interest rate increase for different values of the PMI and input prices (since the start of the financial crisis)
It is instructive to consider three cases.
- Suppose that the PMI were to increase to 63 and input prices remained at 58. If so, the probability of an interest rate increase would rise to 27%. Since the maximum PMI observed in the sample is 62.5, this event seems unlikely to happen.
- Suppose instead that the PMI remained at 56 and input prices rose to 74. If so, the model assigns a probability of 29% to an increase in interest rates. Since the highest observed value of input prices in the sample is 85.3, this is not an entirely unlikely event.
- Suppose that the PMI increases to 58 and input prices to 68, if so the model assigns a probability of 30% to an increase in interest rates.
An increase in input prices thus quickly raises the probability of an interest rate increase, in particular if accompanied by a rise in the PMI.
As noted above, the estimated probability of an increase in interest rates, for any given state of the economy, fell after the onset of the financial crisis. It is therefore interesting to redo the calculations above, assuming that the crisis had not happened. Table 3 shows that, under this assumption, the probability of an interest rate increase in June would have been about 30% instead of 7%. And the estimated probability of an interest rate increase in the three hypothetical cases considered above is about 70%. Thus, given current economic conditions the probability of an interest rate increase has approximately halved because of the change in the ECB’s behaviour.
The main conclusion from Table 3 is thus that if the ECB’s responses to economic conditions were to return to those before the financial crisis struck, the probability of an increase in interest rates would rise markedly, given the current state of the economy.
Table 3 Estimated probability of an interest rate increase for different values of the PMI and input prices (before the start of the financial crisis)
Conclusion
The above analysis of the ECB’s interest rate setting since 1999 has several messages with regard to how interest rates in the Eurozone may evolve in the months to come.
- The likelihood of an interest rate increase, given the current state of the economy, is very low.
- Given how sensitive the ECB’s interest rate decisions have been to the input price variable, and how it has moved in the past, it is likely to be the most important variable determining when the next interest rate increase may come. The PMI is also important, but matters less than input prices.
- Following the onset of the financial crisis, the ECB became less likely to raise interest rates, and more inclined to cut them, given economic conditions. This shift most likely captures the fact that the transmission mechanism of monetary policy weakened, since the focus of the crisis was in the financial sector. Once the ECB judges that the transmission mechanism has reverted to normal, the reaction function may revert to its original form. If so, the probability of an interest rate increase would rise dramatically.
References
Bossone, B and S Labini (2016), “The ECB’s original sin and Franco Modigliani’s long view”, VoxEU, 19 February.
den Haan, W, M Ellison, E Ilzetski, M McMahon and R Reis (2016), “German Council of Economic Experts’ view of ECB policy: Results from the CFM-CEPR Survey”, VoxEU, 9 November.
Gerlach, S (2007), “Interest Rate Setting by the ECB, 1999–2006: Words and Deeds”, International Journal of Central Banking 3(3): 1–45 (also CEPR Discussion Paper No. 4775).
Gerlach, S (2011), “ECB Repo Rate Setting during the Financial Crisis”, Economics Letters 112(2): 186–88 (also CEPR Discussion Paper No. 8346).
Gürkaynak, R (2016), “ECB in Eurozone policymaking: Going forward”, VoxEU, 12 February.
Endnotes
[1] For recent analysis of the ECB’s monetary policy during the crisis, see Bossone and Labini (2016) and Gürkaynak (2016). den Haan et al. (2016) survey economists’ view of the position taken by The German Council of Economic Experts, which has been very hostile to the ECB.
[2] Such data problems can arise from, for instance, poor depersonalisation, faulty working day adjustment, measurement errors, and changes in weighting schemes.
[3] The model is of the ordered logit type of the form estimated by Gerlach (2007, 2011). The regressors are the logarithms of the two variables, and terms interacting them and a dummy variable taking the value of unity from October 2008 onward to capture the impact of the collapse of Lehman. All regressors are highly significant and the pseudo-R squared is 32%.
[4] The p-value indicates that probability that the true value of the parameter is 0. Normally, p-values of 5%, and sometimes 10%, are used to judge statistical significance.
[5] The fact that interest rate changes generally occur when the estimated probabilities are less than 50% is not surprising. For instance, while the probability of having a car accident per hour of driving varies between drivers, road and weather conditions, and time of day, but is always far below 50%.