According to the 2012 UNAIDS report (UNAIDS 2012), 34 million people were living with HIV at the end of 2011. HIV/AIDS is a major cause of death, having killed about 1.7 million people in 2011 alone. The number of new infections was even higher (2.5 million), suggesting an even more severe problem in the future. In order to curb this trend, the United Nations named combatting HIV/AIDS one of its eight Millennium Development Goals.
Sexual HIV transmission accounts for the overwhelming majority of the newly infected. Given such an important topic for policymakers, the natural question is: ‘what are the effective policies?’. Prevention policies have been argued to be more cost-effective than treatment (see Canning 2006). The obvious next question is: ‘which prevention policies have a greater impact?’
In a recent research paper, Greenwood, Kircher, Santos and Tertilt (2013) use some modern tools of quantitative macroeconomics to shed light on the issue. With a calibrated model, the analysis of several policies is conducted. Earlier, purely theoretical work focused on reductions in transmission risk and emphasised that it can lead to higher overall prevalence because people could get excessively risky (see, e.g., Kremer 1996). In its 2012 report, UNAIDS warns that such “potential risk compensation effects are being closely scrutinised, but the dynamics are complex to track” (2012). The constructed model can be used to study precisely these sorts of dynamics.
HIV/AIDS in Africa
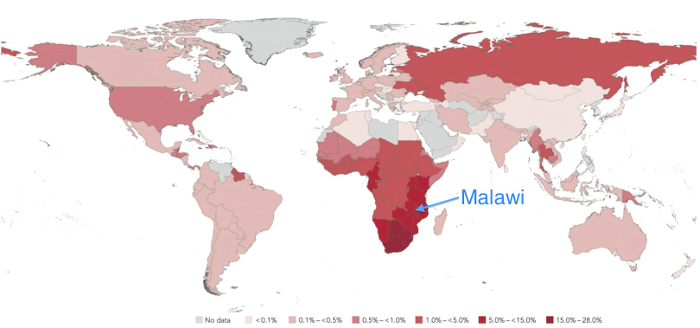
The continent most affected by the epidemic is Africa (see Figure 1), which hosts about two thirds of all HIV/AIDS-infected people. Furthermore, the majority of the HIV-positive population in Africa is female, compared to less than one third in most developed countries (see World Development Indicators). This is due to the fact that most infections in Africa are due to heterosexual sex, the key mechanism in the study surveyed here.
Figure 1. A global view of HIV infection (source: UNAIDS)
The Republic of Malawi has a relatively high HIV/AIDS rate. There is very good data available for Malawi related to both the epidemic and general sexual behavior.1 The facts are clear: 11.8% of the population is infected (10.2% for males and 13.3% for females); sexual behaviour conducive to the spread of the disease is relatively common in Malawi. For example, condoms were used by less than half of all respondents in their last sexual act. The high prevalence of risky behaviour does not necessarily imply that people are uninformed or irrational. In fact, research has shown that people in Malawi are relatively good in assessing their own probability of being infected with HIV (see Delavande and Kohler 2009).
Using economics to model the HIV/AIDS epidemic
Traditionally, two approaches have been taken to study the transmission of HIV/AIDS in Africa: epidemiological studies and field experiments. Epidemiological studies are sophisticated in their treatment of equilibrium but usually lack a feedback loop that captures behavioural responses such as using more condoms when the risk of getting infected is higher. Field experiments are often conducted on a small scale and do not readily allow for the assessment of general equilibrium effects.
The main benefit that economics can bring to the field of epidemiology is the assumption that humans pick their sexual behaviour on the basis of a rational benefit/cost calculation. This assumption allows one to study the potential behavioural responses of individuals with respect to particular policies. Moreover, at the heart of the HIV/AIDS epidemic is an externality, the transmission of a virus. General equilibrium modelling is well suited for the study of externalities. One can analyse how individual shifts in behaviour feed back on each other in equilibrium. Thus, the great advantage of choice-theoretic equilibrium modelling is the joint assessment of both behavioural change and equilibrium adjustment in response to proposed policy interventions.
The model constructed in Greenwood, Kircher, Santos and Tertilt (2013) has three main ingredients:
- First, individuals select the type of sexual activity that they wish to participate in.
They do this based upon beliefs about the riskiness of each type of activity. There are four types of sexual activity. A person may have a long-term relationship with a partner. They may also have short-term relationships. These short-term relationships are further subdivided into ones that use a condom and ones that do not. Finally, a person can select to be abstinent.
- Second, beliefs about the riskiness of various forms of sexual activity are formed rationally.
In the analysis a person's past sexual history is private information. Still, the fact that someone desires, say, a short-run sexual encounter involving no condom may signal something about his past sexual behaviour; for example, just think about someone seeking unprotected sex at an African truck stop. Thus, people form rational forecasts about the likelihood of a partner having HIV/AIDS and the odds of getting HIV/AIDS if s/he engages in a particular type of relationship.
- Third, the analysis is general equilibrium in nature.
There are ‘markets’ for the different types of sexual activities. People have differing tastes over various types of relationships and search accordingly on the various markets to fulfill their desires. They do this recognising that some of these markets will be riskier than others. For example, a short-term relationship using a condom is safer than one that does not.
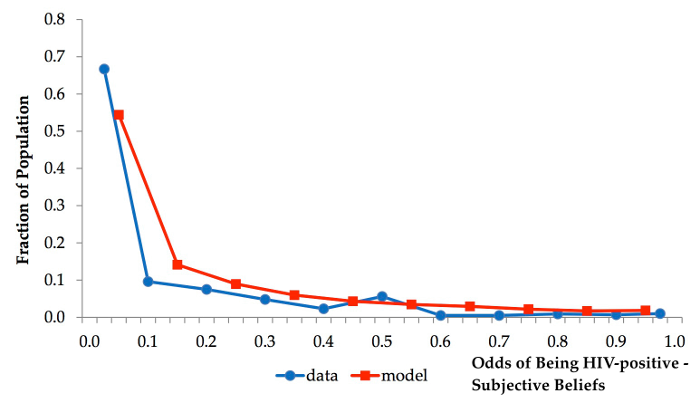
The constructed model is then tuned to fit aspects of the Malawian data. In particular, it is calibrated to match the HIV/AIDS rates for men and women separately, the fraction of sexual relationships that are short-term, the fraction of short-term sexual encounters that use a condom, and the fraction of deaths that arise from HIV/AIDS. The model's ability to match some lifecycle observations is also examined. These include the HIV/AIDS infection rate by age and the likelihood of a casual sexual encounter by age (see Figure 2). The distribution of a symptom-free person's belief about being HIV/AIDS infected is also compared to its data counterpart (see Figure 3). The model does very well at matching the data along these dimensions.
Figure 2. Sexual behavior by age
Figure 3. Distribution of subjective beliefs
Lessons learned
The quantitative part of the study highlights the importance of taking behavioural adjustments and equilibrium effects into account, as they strongly affect the predicted effectiveness of a policy. The relevance of these effects is easy to see when compared to an epidemiological version without behavioural adjustment or small scale interventions without equilibrium effects.2
To be more concrete, consider the effects of a general transmission reduction caused by, say, treating other sexually transmitted diseases. The idea is that the presence of other STDs makes a person more susceptible to contracting HIV. The World Health Organization and UNAIDS consider that sexually transmitted diseases “management continues to be an essential component of HIV prevention programs and should continue to be a key component for AIDS control programs”.3
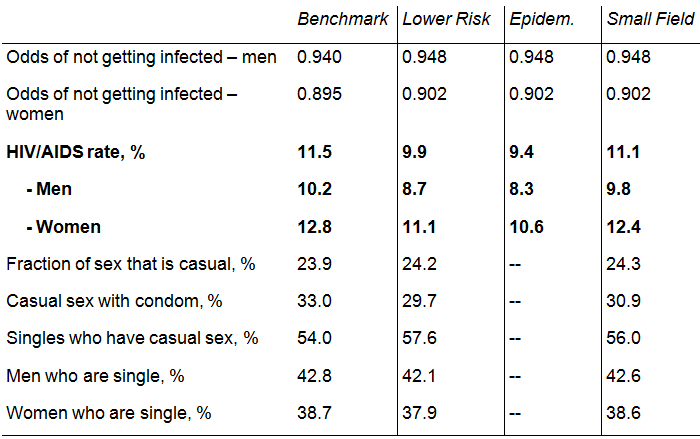
Table 1 shows the simulation results for this policy in the quantitative model. As the transmission risk for both men and women declines by about 13%, the HIV incidence decreases by 1.5 percentage points from 11.5 to 9.9%. Note that this decrease in HIV prevalence masks the finding that agents engage in riskier behaviour. The fraction of sex that is casual increases even though there are less singles around. The reason is that the fraction of non-abstinent singles increases. Moreover, out of the singles having sex, condom usage falls. The upshot of this experiment is that agents can dramatically change their behaviour in response to the policy and that these behavioural changes can have non-trivial effects.
Compare the benchmark results with the epidemiological version of the experiment. In the epidemiological experiment, the decline in HIV prevalence is much larger to 9.4%, a 0.5% difference compared to the benchmark. The reason for this difference is exactly the lack of behavioural changes described above.
The field experiment goes in the opposite direction: it predicts a much smaller decrease in HIV incidence compared to the benchmark. The reason is that, in the field experiment, the reduced number of infections does not lead to an overall decrease in the population prevalence rate. Therefore, it does not feed back into lower infection rates for the treated population. It is interesting to note that eight of the nine studies of sexually transmitted disease treatment for HIV prevention surveyed by Padian et al. (2010) delivered flat results. The simulations presented here highlight a novel reason that may explain these flat results, namely the missing general equilibrium effects in randomised field experiments.
This study also showcases channels beyond the simple effect that some agents increase their risky sexual activity. For example, encouraging marriage may backfire and raise HIV prevalence mainly because some risky people now join the previously safe haven of marriage. While their move towards marriage is usually seen as a reduction in their own risky behaviour, it increases the infection risk for their marriage partners who previously had a higher chance of finding a safe match. Such change in the mixing patterns seriously affects the effectiveness of the policy.
Overall, this research programme aims to develop tools to aid researchers and practitioners in their attempts to think through the various channels that are present in different interventions. Research using computational general equilibrium models to assess the implications that interventions might have on the spread of HIV/AIDS (or other diseases) is in its infancy and results have to be interpreted with caution. However, the model does provide a useful tool for elaborate thought experiments to discover areas that might need further investigation.
Table 1. Treating other sexually transmitted diseases
References
Canning, David (2006), “The Economics of HIV/AIDS in Low-Income Countries: The Case for Prevention”, Journal of Economic Perspectives 20(3), 212-142.
Delavande, Adeline and Hans-Peter Kohler (2009), “Subjective Expectations in the Context of HIV/AIDS in Malawi”, Demographic Research 20, 817-874.
Greenwood, Jeremy, Philipp Kircher, Cezar Santos, and Michèle Tertilt (2013), “An Equilibrium Model of the African HIV/AIDS Epidemic”, CEPR Discussion Paper 9423, London, Centre for Economic Policy Research.
Grosskurth, H, F Mosha, J Todd, E Mwijarubi, A Klokke, K Senkoro, P Mayaud, J Changalucha, A Nicoll, J ka Gina, G, Newell, K Mugeye, D Mabey, and R Hayes (1995), “Impact of Improved Treatment of Sexually Transmitted Diseases on HIV Infection in Rural Tanzania: Randomized Controlled Trial”, Lancet 346(8974), 530–536.
Kremer, Michael (1996), “Integrating Behavioral Choice into Epidemiological Models of AIDS”, The Quarterly Journal of Economics 111(2), 549-573.
Oster, Emily (2005), “Sexually Transmitted Infections, Sexual Behavior, and the HIV/AIDS Epidemic”, The Quarterly Journal of Economics 120(2), 467–515.
Padian, Nancy S, S I McCoy, J E Balkus, and J N Wasserheit (2010), “Weighing the Gold in the Gold Standard: Challenges in HIV Prevention Research”, AIDS 24(5), 621-635.
UNAIDS (2012), Report on the Global AIDS Epidemic.
UNAIDS/WHO (2000), “Consultation on STD Interventions for Preventing HIV: What is the Evidence?”.
World Development Indicators, website, World Bank.
1 The data for Malawi come from the micro data of the Demographic and Health Survey (DHS) in 2004.
2 In the model, the field experiment assumes that only a small fraction of the population is treated and changes their behavior, but that this fraction interacts in equilibrium with everyone else at pre-existing infection rates. The epidemiological experiment assumes that people make no behavioral adjustments and therefore uses the policy functions from the benchmark calibration but the infection probabilities and assessments of transmission risks are governed by the new transmission probabilities.
3 See UNAIDS/WHO (2000). For other studies regarding the relationship between HIV/AIDS and other STDs, see Oster (2005) and Grosskurth et al. (1995).