Comparing price levels to infer the proper currency value is one way to measure the degree of currency misalignment. Absolute purchasing power parity is one particularly simple – and particularly inappropriate – price criterion. The proposition that similar bundles of goods should be equally priced when denominated in a common currency is frequently violated.
A more commonly used criterion is the Penn effect (Summers and Heston 1991). The finding that the price level is higher in countries with a higher per capita income is one of the most well-documented empirical regularities in international finance. It is consistent with a variety of theoretical frameworks, including a Balassa-Samuelson mechanism, and demand-side forces (for example, a preference for non-tradable goods at higher incomes).
Our research has investigated whether the Penn effect is as robust as is typically conceived (Cheung et al. 2016, following Cheung et al. 2007). Testing for the Penn effect has been hampered because price data are often not measured precisely. This means that new versions of the data can create different results.
Where does the Penn effect come from?
If the law of one price holds, summing over all goods, and assuming the weights associated with each good are the same in both the home country and foreign country basket, then we obtain the absolute purchasing power parity condition. This is, the price level in one country equals the price level in another country, converted into common currency units by the exchange rate.
If the weights differ between home and foreign country baskets (or production bundles) then, even if the law of one price holds, absolute purchasing power parity need not hold. The construction of the price level variable in the Penn World Tables (PWT), and other purchasing power parity exchange rates, attempts to circumvent this problem by using prices (not price indices) of goods. They calculate the aggregate price level using the same weights.
If some share of the basket is non-tradable, the real exchange rate can rise as changes occur in the relative price of traded goods between countries, or as the relative price of non-tradables rises in one country relative to another. Supply-side factors such as productivity (Balassa 1964, Samuelson 1964) or demand-side factors could have an influence, but productivity has been the dominant focus. Productivity is assumed to be higher in the tradable sector in higher income countries. This gives rise to the Penn effect.
Updating the results
For our baseline results, we rely upon price level and per capita income data from the PWT 8.1 (Feenstra et al. 2013). We also cross-check our results using the World Bank’s World Development Indicators (WDI).
Running a regression of the price level on per capita income (relative to the US) using the full dataset of approximately 150 countries between 1970 and 2011, there is a positive coefficient on per capita income. This supports the conventional wisdom. (The sample excludes some small countries, some oil exporters with extreme price levels, and country-observations that encompass hyperinflation.)
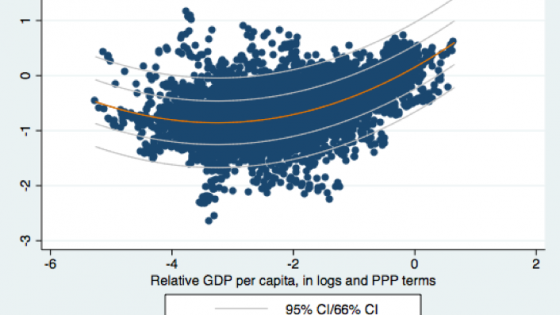
But Kessler and Subramanian (2014) and Hassan (forthcoming) argue that the relationship is nonlinear, even expressed in log terms. Therefore, we also investigated whether there is a quadratic link between income and real exchange rate. Figure 1 shows the Penn effect relationship for full sample. Just eyeballing the figure, it doesn't look linear. A quadratic specification gives a U-shaped relationship in which the coefficients on the linear and square terms are statistically significant. In addition, a formal test for a U-shaped curve (Lind and Mehlum 2010) rejects the 'no-U shape' null hypothesis.
Figure 1 Scatter plot of full sample and quadratic fit
Figure 1 shows the regression lines and confidence intervals for the fitted curve. Its minimum is at the relative GDP per capita value of -3.25, which matches Bangladesh in 2009.
This non-linear relationship is apparent in the previous version of the PWT (7.0), as well as the WDI. It also shows up in the subsample for non-advanced economies. Interestingly, the coefficient on the square term takes on a negative value for advanced economies.
It is, however, unsatisfying to have a non-linear relationship that is not explicitly linked to economic factors. It makes sense to see if the U-shape is still there when additional control variables are included in the regression. Including covariates like corruption or an oil exporter dummy, we still find the U-shaped relationship. Both variables raise the price level (appreciate the currency) for developing countries. For a sample of only these countries, the evidence for a U-shape is weaker. The test fails to reject the 'no U-shape' null hypothesis.
Measuring renminbi misalignment
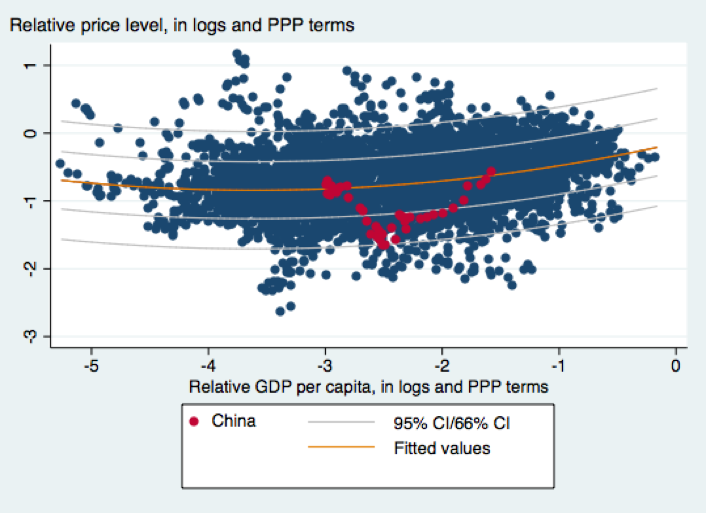
One can obtain a variety of estimates by varying sample and specification. Using the most basic estimate of the non-linear relationship, estimated over the developing country subsample, we find that in 2011 the Chinese currency (RMB) was approximately at the level predicted by the regression. This is shown in Figure 2, which displays the scatterplot for developing countries and the quadratic fit.
Figure 2 Quadratic fit for developing countries
The red circles are observations for China. The observation furthest to the right is for 2011, and is on the regression line. Of course the fit is imprecise, and the currency could be substantially overvalued or undervalued. Nonetheless, the situation was different in 2005, when the RMB was well below the expected level.
At China’s 2011 income level the degree of misalignment does not depend much on whether we use the linear or quadratic specification, nor on whether we use the full sample or developing countries only. Rather, the estimates are sensitive to the use of either the Penn World Tables or the World Development Indicators. In all instances though, the Chinese currency was undervalued in 2005, and it has since moved toward overvaluation.
References
Balassa, B. (1964) “The Purchasing Power Parity Doctrine: A Reappraisal”, Journal of Political Economy 72, 584-596.
Cheung, Y.-W., M. Chinn and E. Fujii (2007) “The Overvaluation of Renminbi Undervaluation”, Journal of International Money and Finance 26(5), 762-785.
Cheung, Y.-W., M. Chinn and X. Nong (2016) “Estimating Currency Misalignment Using the Penn Effect: It’s Not as Simple as It Looks”, NBER Working Paper No. 22539.
Feenstra, R. C., R. Inklaar and M. Timmer (2013) “PWT 8.0–a user guide”, Groningen Growth and Development Centre, University of Groningen.
Hassan, F. (forthcoming), “The price of development”, Journal of International Economics.
Kessler, M. and A. Subramanian (2014) “Is the renminbi still undervalued? Not according to new PPP estimate”, RealTime Economic Issues Watch.
Lind, J.T. and H. Mehlum (2009) “With or Without U? The Appropriate Test for a U-Shaped Relationship”, Oxford Bulletin of Economics and Statistics 72(1) 109-118.
Samuelson, P. (1964) “Theoretical Notes on Trade Problems”, Review of Economics and Statistics 46, 145-154.
Summers, R. and A. Heston (1991) “The Penn World Table (Mark 5): An Expanded Set of International Comparisons”, Quarterly Journal of Economics 106, 327-68.