Governments have imposed unprecedented economic shutdowns to thwart the spread of Covid-19. These policies range from discouraging large gatherings to outright closures of non-essential businesses. Lockdowns have slowed the spread of the virus (Hsiang et al. 2020, Fang et al. 2020) but at considerable economic costs (Deb et al. 2020 Torrejón Pérez et al. 2020).
In implementing lockdowns, policymakers have primarily imposed the same policies uniformly across locations within a city – for instance, non-essential businesses across entire cities have been closed at the same time. Even across border states in the US, the average difference in the timing of lockdown policies has been just four days.
However, the spatial density of economic activity is not uniform across a city. Residents commute to central business districts where jobs are located. On a typical day, the daytime population of Manhattan is twice as large as its night-time population as residents from the other boroughs and neighbouring counties commute into Manhattan for work. When the spread of a disease depends on the number and proximity of human interactions, some locations are more likely to spread the disease than others. At the same time, closing some locations may have larger economic costs.
In Fajgelbaum et al. (2020), we study optimal dynamic policies to fight pandemics in a commuting network.1 The framework integrates standard spatial epidemiology and trade models. The epidemiology block of the model shows how a virus spreads through commuters (either at the workplace or via public transit). The trade block of the model shows how lockdown policies reduce the real income of workers who stay at home and, indirectly, impact other locations as these workers consume fewer goods or services.
We use the model to answer three questions:
1. What are the optimal lockdown patterns over time and space?
2. How large are the benefits of optimal spatial targeting?
3. How do observed commuting reductions compare with optimal?
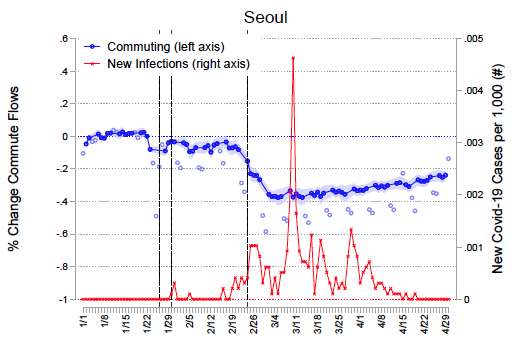
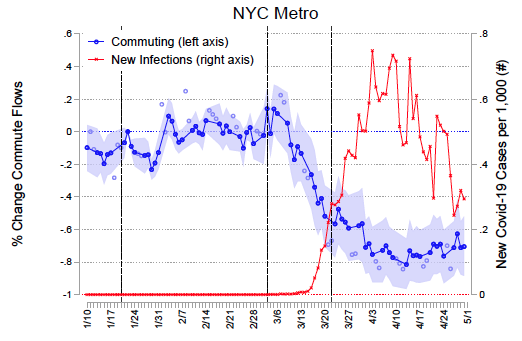
We estimate the model's parameters in three cities that experienced varying degrees of the initial Covid-19 shock: Seoul, Daegu, and the New York metropolitan area (henceforth, “New York”). We study Korea because of its high rate of testing since the onset of the pandemic and its availability of real-time public transit commuting and credit-card expenditure data. The latter serve to estimate spatial frictions that determine how income shocks due to lockdown policies diffuse across space. We study New York because of the large initial spread of Covid-19 and its economic importance, with commuting flows measured by mobile phone mobility. Figure 1 demonstrates the spread of the virus in each city against the dramatic fall in commuting induced either by precautionary behaviour, strongly encouraged social distancing (as in Korea), or mandated lockdowns (as in New York).
Figure 1 Commuting response and disease spread
Panel a Daegu
Panel b Seoul
Panel c New York
Note: Figure reports the average daily changes in commute flows relative to the pre-pandemic levels (normalised to 1 on January 22, 2020). Weekdays (weekends/holidays) are denoted in darker (lighter) blue circles. The sample size is 968 for Daegu, 75,625 for Seoul, and 46,325 for New York. Each observation is a district by date pair for Daegu and a district/county-pair by date tuple for Seoul and New York from January 1, 2020 to April 30. The first vertical line denotes the date of the first case in Korea (top/middle) and the US (bottom). The middle and the last vertical lines denote the date of the first case and the lockdown announcement in each city, respectively. Wild bootstrap standard errors are clustered by district for Daegu, and two-way-clustered by origin and destination for Seoul and New York. Error bars show 95% confidence intervals. The right axis reports the daily new Covid-19 cases in Daegu (top), Seoul (middle) and New York (bottom). See Fajgelbaum et al. (2020) for details.
Our paper has three results
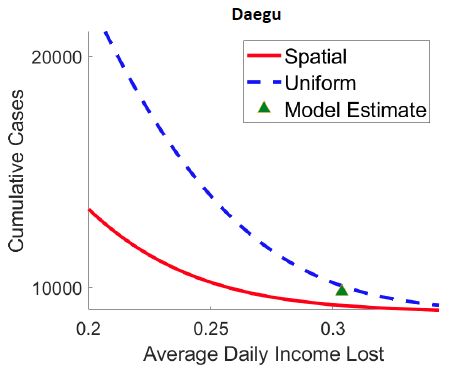
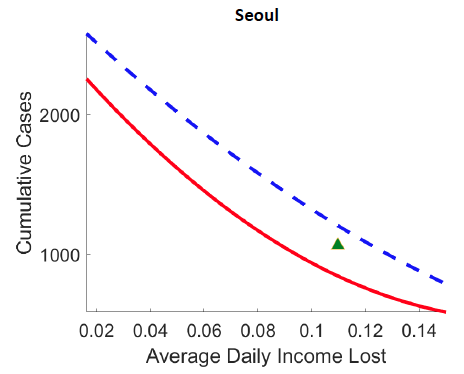
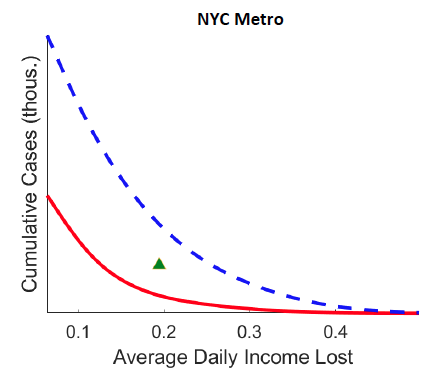
1. Figure 2 demonstrates that optimal spatial lockdowns have much smaller economic costs than uniform lockdowns. For any given level of Covid-19 cases (y-axis), an optimal spatially targeted lockdown yields smaller economic loss (daily income lost, x-axis) than the optimal uniform policy (i.e. with same lockdown in space). Given the actual case count and economic costs estimated by the model on 30 April, our model predicts that a targeted lockdown could reduce economic losses by 15%, 28%, and 50% in Daegu, Seoul, and New York, respectively.
Figure 2 Pareto frontiers: Spatially targeted versus uniform lockdowns
Panel a Daegu
Panel b Seoul
Panel c New York
Note: Figure plots the cumulative number of new cases (y-axis, log scale) and the average real income lost per day between the date of the first confirmed case and April 30, 2020 for parameterization of the value of life ranging from 1/100 to 100 times the benchmark (i.e. $10 million) in both the optimal lockdown with space and time variation (referred to as “Spatial”) and in the spatially uniform optimal solution with time variation only (“Uniform”, i.e., the same lockdown across all locations). The green triangle shows the case count and real income lost implied by the estimated model on 30 April 2020.
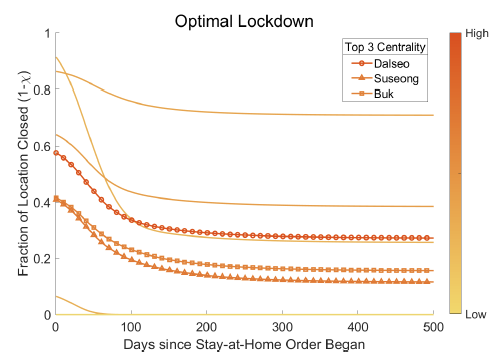
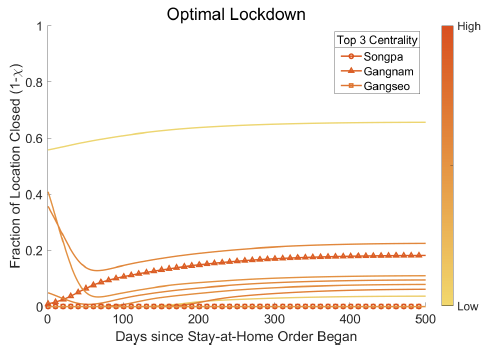
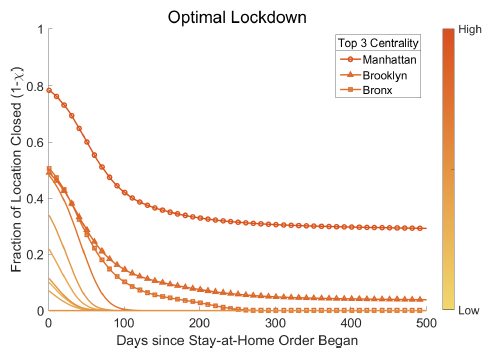
2. Figure 3 demonstrates that the optimal lockdown may require a strict initial lockdown in the most central locations, which is then relaxed over time. However, the optimal lockdown is not as simple as shutting down ‘highly central’ nodes within a commuting network. Instead, the optimal lockdown depends on the spatial distribution of commutes, real income, and initial (i.e. pre-lockdown) virus spread. For instance, commuters from a home district where Covid-19 cases are rising are more likely to carry the virus to their workplace. The probability of these commuters infecting others is higher in denser workplaces as these places are more likely to have increased incidences and intensity of social interactions. The optimal lockdown trades off the economic costs against the potential for diffusion of each location.
Figure 3 Centrality of commuting locations and optimal policies
Panel a Daegu
Panel b Seoul
Panel c New York
Notes: Figure plots the optimal policies over time for each location in the network. The floor of the line represents the centrality of the location in the network. The three most central locations in the network are indicated in the legend. See Fajgelbaum et al. (2020) for details.
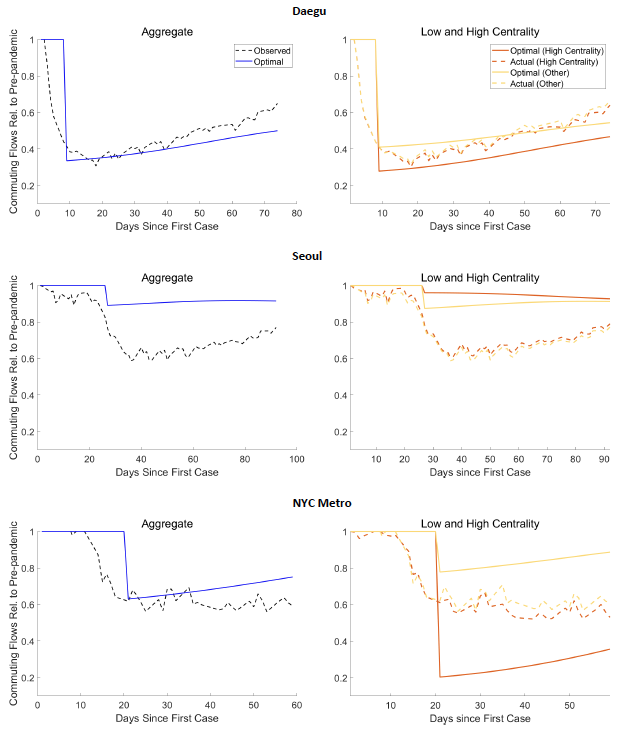
3. Figure 4 compares actual commute responses to the optimal benchmarks in the three cities. The left panel compares the aggregate commuting flows observed in the data to the (predicted) aggregate flows under an optimal spatial lockdown. For Daegu and New York, the two series are close to the model’s prediction. So, where do the gains from a spatially targeted lockdown come from? The right panel of Figure 4 reports commuting flows by high- and low-centrality locations. The time series of observed commute flows in high- and low-centrality locations are quite similar. In contrast, spatial lockdowns would impose very different commute paths in Daegu and New York, two cities that experienced a large initial virus spread. Our results suggest that the total case counts and economic losses would have been smaller in these two cities if the commuting reduction had been stronger in more central areas and weaker in less central areas. In the case of Seoul, which experienced a significantly smaller shock, the observed decreases in commuting were larger than the optimal prediction across all locations.
Figure 4 Changes in commuting flows: Optimal and observed
Note: In the left panels, the dashed black line shows the aggregate commuting flows in each city starting from the date of the first confirmed case in each city. The solid and circled blue lines show the aggregate commute flows implied by the optimal spatial policy. In the right panels, optimal and observed commuting responses are divided by top-three centrality locations (darker shade) and the other locations.
Our framework could be applied at coarser or finer spatial scales to inform the current debate over whether to restrict travel from states, and if so from which states.
References
Alvarez, F, D Argente, and F Lippi (2020), “A simple planning problem for COVID-19 lockdown”, NBER Working Paper 26981.
Deb, P, D Furceri, J D Ostry and N Tawk (2020), “COVID-induced economic uncertainty and its consequences”, VoxEU.org, 17 June.
Fajgelbaum, P, A Khandelwal, W Kim, C Mantovani and E Schaal. (2020), “Optimal lockdown in a commuting network”, NBER Working Paper 27441.
Fang, H, L Wang and Y Yang (2020), “Human mobility restrictions and the spread of the novel coronavirus (2019-ncov) in China”, NBER Working Paper 26906.
Hsiang, S, D Allen, S Annan-Phan, K Bell, I Bolliger, T Chong, H Druckenmiller, L Y Huang, A Hultgren, E Krasovich, et al. (2020), “The effect of large-scale anti-contagion policies on the COVID-19 pandemic”, Nature, 1-9.
Monras, J (2020), “Some thoughts on COVID-19 from a labour mobility perspective: From ‘red-zoning’ to ‘green-zoning’”, VoxEU.org, 25 March.
Piguillem, F and L Shi (2020), “The optimal COVID-19 quarantine and testing policies”, Working Paper.
Rowthorn, R and F Toxvaerd (2020), “The optimal control of infectious diseases via prevention and treatment”, Cambridge Working Papers in Economics 2027.
Torrejón Pérez, S, M Fana, I González-Vázquez and E Fernández-Macías (2020), “The asymmetric impact of COVID-19 confinement measures on EU labour markets”, VoxEU.org, 8 May.
Endnotes
1 Recent studies such as Alvarez et al. (2020), Piguillem and Shi (2020) and Rowthorn and Toxvaerd (2020), among others, have studied optimal policies in a single-location setting (e.g. a country or a city). Acemoglu et al. (2020), Baqaee et al. (2020), and Glover et al. (2020), among others, study lockdown with heterogeneous agents. A VoxEU column by Monras (2020) suggests policies could be targeted at commuting zones.