Over the past decade, advanced economy exchange rates have exhibited substantial variability, even as conventional empirical determinants – such as interest rates and inflation – have remained fairly stable. At the same, the Global Crisis was associated with unprecedented levels of risk and illiquidity, with obvious effects on financial markets. These developments call for a systematic assessment of exchange rate models.1
One way of assessing the relative empirical content of differing exchange rate models is by way of a horserace approach: see which model performs the best in predicting the actual level of the exchange rate when the determinants are assumed to be known. This approach has a long history, beginning with the work of Meese and Rogoff (1983). Earlier studies focused on a fairly narrow set of models, including ones where interest rate differentials, monetary factors, and foreign debt mattered. In more recent studies (Cheung et al. 2005) this set of models was augmented by those including a role for price levels, for productivity growth, and a composite specification incorporating several different channels whereby debt, productivity, and interest rates matter (i.e. behavioural equilibrium exchange rate, or BEER, models) – all with little success.
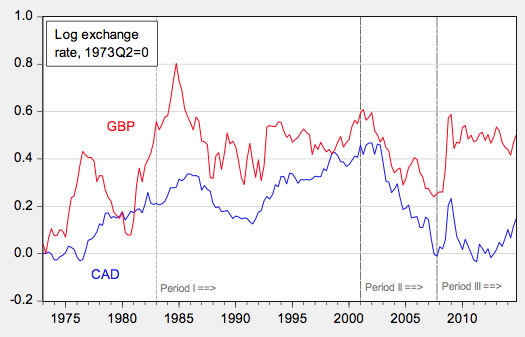
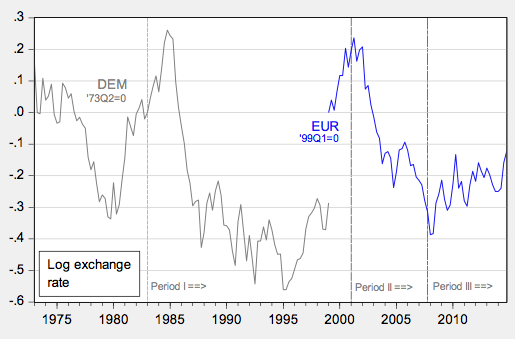
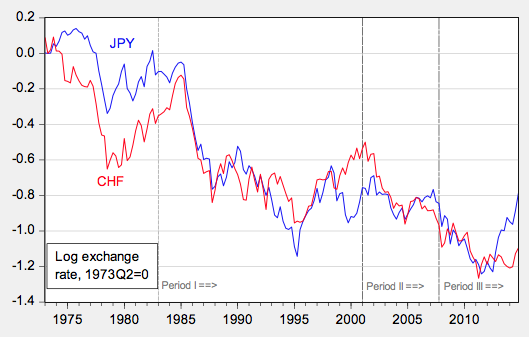
In our recent paper, we examine the British pound, the Canadian dollar, the euro, the Japanese yen, and the Swiss franc, all against the US dollar (Cheung et al. 2017). The euro is newly included relative to our 2005 paper, supplanting the Deutsche mark. These exchange rates are shown in Figures 1-3.
Figure 1. Exchange rates for Canadian dollar and British pound, end of month
Figure 2. Exchange rates for Deutsche mark and euro, end of month
Figure 3. Exchange rates for Japanese yen and Swiss franc, end of month
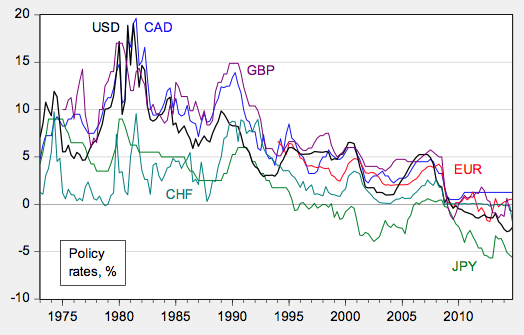
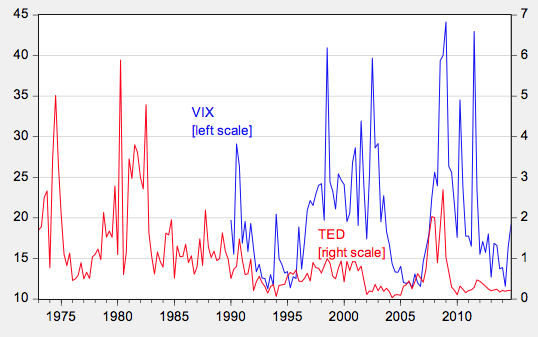
The set of models is further expanded to include the factors that central banks are believed to pay attention to – so called ‘Taylor rule fundamentals’ (e.g. Molodtsova and Papell 2009) such as the degree of slack in the economy, and the inflation rate – the difference between short and long term interest rates – sometimes called the slope of the yield curve (e.g., Chen and Tsang 2013). In this study, the analysis also addresses the special factors that have characterised the world economy over the last decade, including the fact that it is difficult to set interest rates much below zero (i.e. the advent of the zero lower bound), and the rise of importance in risk and liquidity in global financial markets. We account for the former by use of ‘shadow interest rates’ – that is, the short-term interest rate that is consistent with longer term interest rates (shown in Figure 4). We account for the latter by augmenting standard models based on monetary fundamentals with measures of risk, namely the VIX and the TED spread (shown in Figure 5).
Figure 4. Overnight interest rates and shadow rates
Figure 5. VIX (left scale) and TED spread (right scale)
The performance of each of these models is compared against the ‘no change’, or random walk, benchmark and over different time horizons (one quarter, one year, five years), using differing metrics. The first metric is whether the variability of the predictions around the actual values is greater than or less than that obtained by a ‘no-change prediction’. This is a comparison of the mean squared error of a model against a random walk model. The second metric is a direction of change comparison: Does the predicted change in the value of the exchange rate match the actual change? The third metric is a ‘consistency’ test, proposed in Cheung and Chinn (1998). This test requires that the predicted value and the actual exchange rate share the same trend.
Because the forms of the relationships are not known, we use two specifications. The first is assumes that the level of the exchange rate is related to the level of explanatory variables over the long term. Under this approach, if the level of the exchange rate is below the level predicted in the long run by the explanatory variables, then the exchange rate will be predicted to rise. The second is to assume the growth rate of the exchange rate as depending on the growth rate of the explanatory variables.
Finally, in order to ensure that our findings are not being driven by our selection of time periods, we conduct comparisons over three different periods, as shown in Figures 1-3:
1. The period after the US disinflation (starting in 1983);
2. The period after the dot.com boom (starting in 2001); and
3. The period starting with the beginning of the Great Recession (the end of 2007).
In summary, no model consistently outperforms a no-change – or random walk – prediction by a mean squared error measure, although the model that predicts a relationship between differences in price levels and the exchange rate – purchasing power parity – does fairly well. Further, specifications incorporating long-run relationships in levels tend to outperform specifications involving growth rates, particularly along the mean squared error dimension.
The models that have become popular in the last 15 years or so might not be much better than the older ones. Overall, the results do not point to any given model/specification combination as being very successful in either the mean squared error or consistency criteria. On the other hand, many models seem to do well, particularly using the direction of change criterion.
Of the economic models, purchasing power parity and interest rate parity do fairly well, perhaps due to the parsimoniousness of the specifications (interest rate parity requires no parameter estimation). In the most recent period, accounting for risk and liquidity tends to improve the fit of the workhorse sticky price monetary model, even if the predictive power is still unimpressive. But in general the more recent models do not consistently outperform older ones, even when assessed on the recent, post-crisis period.
The euro/dollar exchange rate appears particularly difficult to predict, using the models examined in this study. This outcome is likely attributable to the short span of data available for precisely estimating the empirical relationships.
References
Chen, Y-C and K P Tsang (2013), “What does the yield curve tell us about exchange rate predictability”, Review of Economics and Statistics 95(1): 185-205.
Cheung, Y-W and M Chinn (1998), “Integration, cointegration, and the forecast consistency of structural exchange rate models”, Journal of International Money and Finance 17(5): 813–830.
Cheung, Y-W, M Chinn and A G Pascual (2005) “Empirical exchange rate models of the nineties: Are any fit to survive?”, Journal of International Money and Finance 24(November): 1150-1175.
Cheung, Y-W, M Chinn, A G Pascual and Y Zhang (2017), “Exchange rate prediction: New models, new data, new currencies?”, NBER, Working paper 23267 (March).
Engel, C (2014), “Exchange rates and interest parity”, Handbook of International Economics, 4(Elsevier): 453-522.
Meese, R and K Rogoff (1983), “Empirical exchange rate models of the seventies: Do they fit out of sample?”, Journal of International Economics 14: 3-24.
Molodtsova, T and D H Papell (2009), "Out-of-sample exchange rate predictability with taylor rule fundamentals", Journal of International Economics 77(2): 167-180.
Rossi, B (2013) “Exchange rate predictability”, Journal of Economic Literature 51(4): 1063-1119.
Endnotes
[1] See also surveys by Engel (2014) and Rossi (2013).