Although few would disagree that today’s world cannot afford to misread China’s growth performance, China’s long-debated GDP data problem has remained inconclusive. While some studies suggest that official growth estimates tend to cover up external shocks, smooth out volatilities, and hence exaggerate China’s real growth, some claim that they are reasonably reliable and even have improved over the past decade. The debate is largely attributable to a widely used physical indicator approach that aims to gauge China’s growth performance while bypassing the official unreliable price data. However, regardless of the physical indicator - energy consumed, commodities produced, cargo handled, bank loans made, or night-time lights recorded – such an approach cannot integrate its alternative estimates with a productivity theory-based macroeconomic framework in which economists and national accountants can communicate with a common language.
The hidden price effect hypothesis
Observers of the Chinese economy have long argued that China’s practices in price statistics are the major barrier to a more reliable measure of China’s real growth performance. Among the earlier researchers, Field (1992), after identifying obvious flaws in official farm output data due to the ambiguity between current and constant prices, conjectured that China’s growth rates contained a serious upward bias. Rawski (1993), with a careful investigation, also denounced Chinese price data on industrial output. Woo (1996) and Maddison (1998) went further, suggesting that the institutional mishandling of constant and current prices began at the enterprise level and then influenced the entire system. These studies nurtured a hidden price effect hypothesis for China’s official growth rate and encouraged a search for alternative physical indicators to circumvent the price effect.
Unlike earlier researchers, Maddison realised that the physical indicator approach must be made systemic in line with the System of National Accounts (SNA) framework. He used commodity-based volume estimates for agriculture and industry and incorporated them into national input-output accounts, but allowed official estimates for the rest of the economy to remain intact in the absence of alternative information (excepting what he called ‘non-material’ services for which the number of workers was used as a proxy). Maddison (1998) arrived at a growth rate of 7.5% per annum for the period 1978-1995, which was 2.3 percentage points slower than that of China’s National Bureau of Statistics (NBS 2019). This finding appears to be robust after being supported by subsequent studies with updated data and refined methodologies (Maddison and Wu 2008, Wu 2013).
Our approach to directly addressing the price problem
Although Maddison’s work is superior to those of others who also use the physical indicator approach, it shed no light on the role of prices in China’s growth. Besides, its physical nature is by no means easier than others in communicating with national accountants and economists at large. It would be nonetheless wrong to conclude that the gap between Maddison’s real growth and the official nominal growth is a pure price effect with little information on how price data are collected, if and to what extent institutional deficiencies affect the pricing process, how output prices change relative to input prices, and how the deflated outputs of industries are aggregated.
Conceptually, the gap between the underlying real growth rate, likely closer to Maddison’s estimate rather than the official estimate, and the reported ‘real growth rate’ by the statistical authorities is composed of three major biases. These are the use of a single deflation approach when actual changes of input prices differ significantly from those of output prices, a constant price value (CPV)-based aggregation that inevitably introduces substitution bias, and data problems caused by all types of manipulations. We propose a national accounts approach to addressing the first two biases. Using China’s input-output tables (CIOTs) in time series and matching producer prices indices (PPI) matrices for the 37 economy-wide industries based on Wu and Ito (2015), revised and updated, we conduct double deflation at the industry level to correct a long-standing single-deflation bias embedded in official data, and then use a Törnqvist index approach to correct substitution biases embedded in the official CPV aggregation to obtain an alternative real growth rate for China.
An assessment of the official GDP deflators
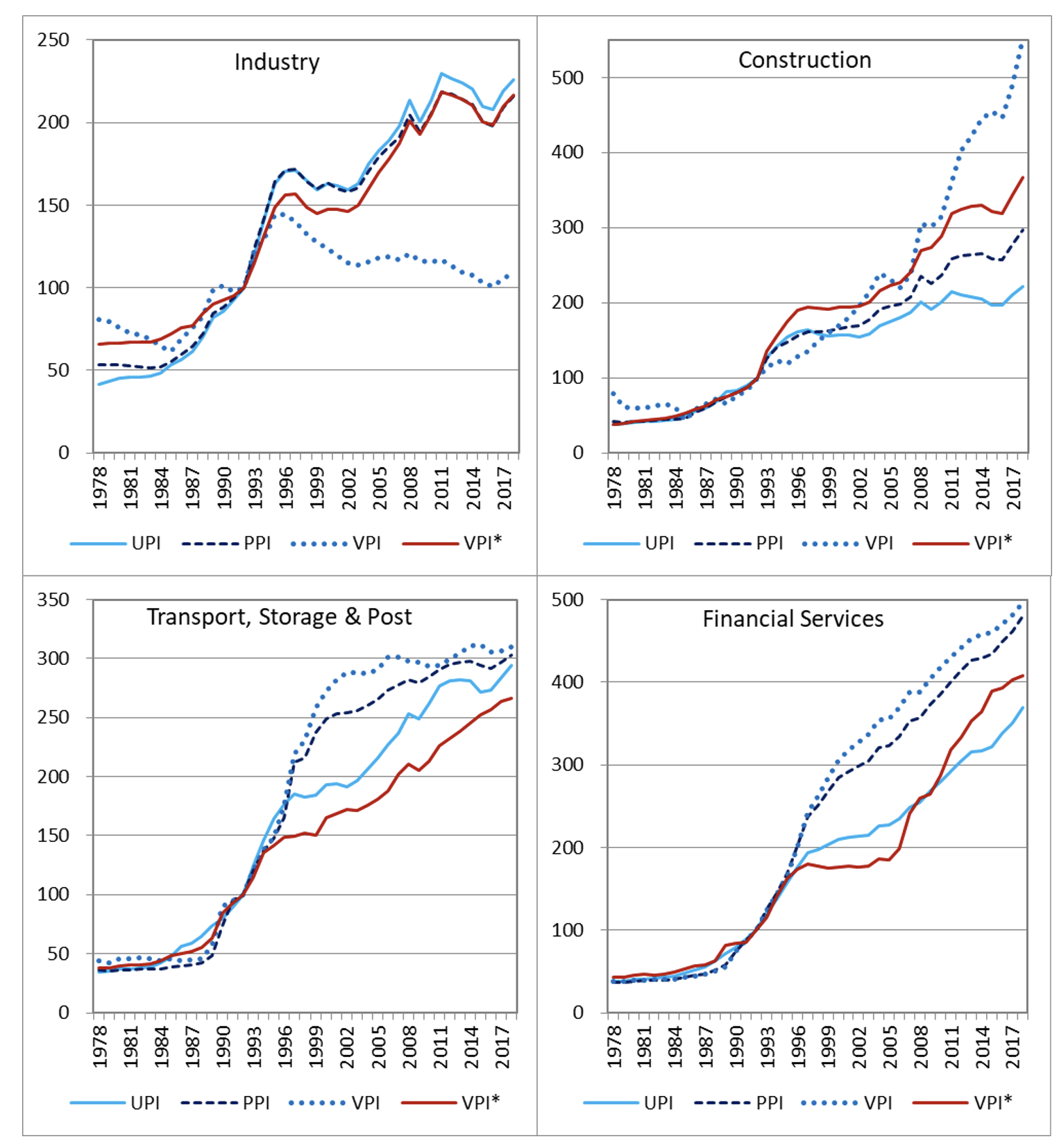
With the time-series CIOTs, PPI matrices are used to systematically generate price indices for purchasers or users, termed as user price indices (UPIs), by cost weighting the PPIs of all input-producing industries for each input-using industry. The examples shown in Figure 1 clearly indicate that changes in UPIs do not follow changes in PPIs and the discrepancies between the two differ significantly across industries. An implicit price index for value added (VPI) can also be derived for each industry. As expected, we see that changes in VPIs do not follow those in PPIs and UPIs, supporting the hypothesis that predicts the existence of the inequality if the perfect market assumption is not held (David 1966, Hulten 1973). This can help us assess the NBS value-added price index underlying its GDP accounts, denoted as VPI*.
Figure 1 Gauging price changes in the Chinese economy, selected sectors: Constructed PPI and IOT-derived UPI and VPI in comparison with official VPI*
Source: Selected from Figure 2 in Wu and Li (2021).
We begin with an assumption that NBS uses a single deflation method, thus an implicit equality is held, VPI*=PPI*=UPI*. Then, a comparison of our PPIs with official VPI*s should be equivalent to a comparison of two sets of PPIs. The hidden price effect hypothesis suggests that official price statistics are downward biased, hence exaggerating China’s real growth. In a further adjustment to PPI, we therefore assume that for any industry, a more rapid output price increase is closer to the reality, either by official VPI* (= PPI*) or by our alternative PPI.
Our solutions to the deflation and aggregation problems
In theory, a single deflation approach requires stringent assumptions such as constant-returns-to-scale technology and perfect competition in both intermediate and final goods and services markets (David 1966, Hulten 1973, Sato 1976). In the Chinese reality, given various market distortions, it is naïve to assume that changes in input prices are the same as changes in output prices. If the former is slower than the latter – or in other words, the real input grows more rapidly than the real output – holding others unchanged, the estimated growth rate will be upward biased. Therefore, to better capture price changes of both outputs and inputs, a double deflation method should be used as recommended by statistical agencies of international organizations (United Nations 2009, OECD 2001, European Communities, 2008).
The aggregation of the final outputs of industries is an unavoidable step before obtaining a growth rate for the total economy. The official usual practice is to choose a ‘base year’ for a price index to obtain a real output first for each industry, and then to sum up the results of all industries to achieve a national total real output. Yet, no choice of the base year, regardless of the nature of the index – Laspeyres or Paasche – is free of substitution bias caused by fixed weights of industries despite rapid changes of industrial structure. This aggregation problem can be addressed by a Divisia index, a theoretical construct that incorporates quantity and price changes over time from subcomponents that are measured in different units, and to summarise them in a time series of the changes in quantities. In practice, since economic data are not measured in continuous time, the Törnqvist index procedures, adopted in this study, make a close analogue in discrete time periods.
Interpreting the results
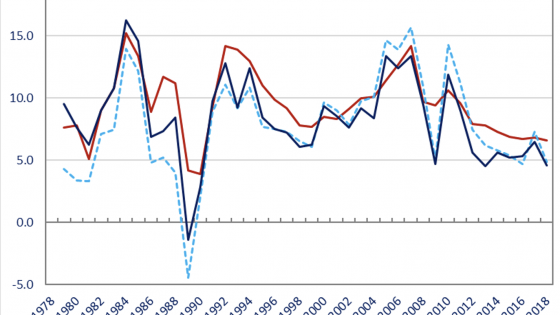
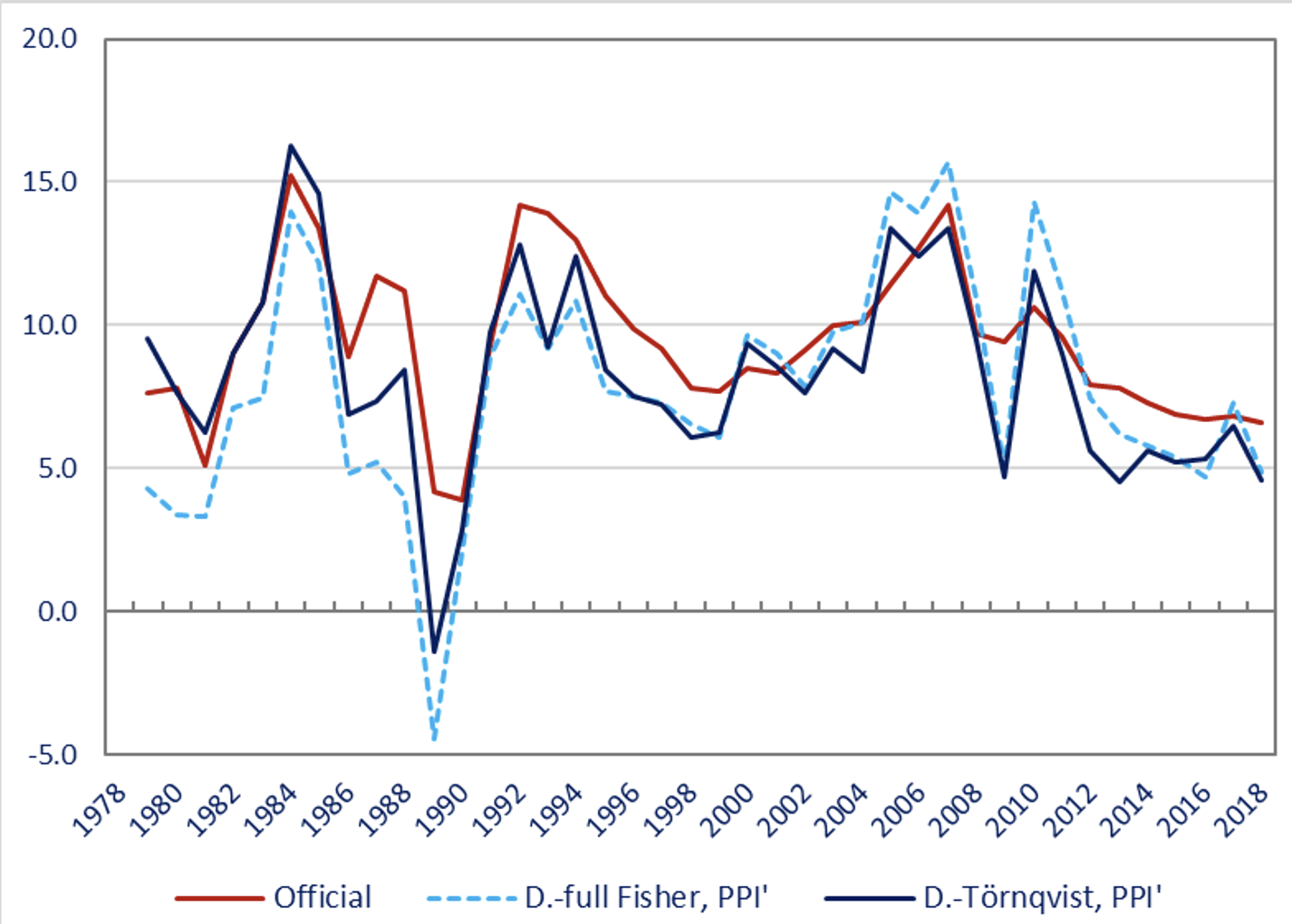
We benchmark our alternative estimates on the official GDP growth at 9.5% per annum (Figure 2). With a segmented Fisher index approach to the series obtained by the Laspeyres index with different base years and single deflation, we show that the so-estimated growth rate is 9.3% per annum if using the official deflators, but it reduces to 8.5% if using our alternative deflators. Then, if changing to a double deflation approach, ceteris paribus, the growth will be even slower, down to 8.1% per annum, and if using a segmented Fisher index, the growth rate will be further reduced to 7.8% per annum (D.-full Fisher, Figure 2). However, when applying a Törnqvist approach to the problem, that is, aggregating the nominal output-weighted growth estimates of all industries, still sticking to the double deflation approach and our reconstructed deflators, we arrive at a growth rate of 8.3% per annum (D.- Törnqvist, Figure 2). This means that the Törnqvist correction for substitution biases does not necessarily reduce the growth rate on average. These is nonetheless no case in which we could obtain an average growth rate for the period in question that is closer to the official estimate without violating the theory of deflation and aggregation. This clearly suggests that the official growth rate is surely exaggerated from a methodological perspective, regardless of the likelihood of data manipulations.
Figure 2 China’s growth performance reassessed (annual GDP growth in %)
Source: Figure 4 in Wu and Li (2021).
Concluding remarks
Our major contribution is to bring the deflation and aggregation procedures firmly in line with the productivity theory and have them empirically conform to the national accounts. Compared to the official estimates, our procedures have not only exposed more volatile movements and greater impacts of external shocks, but also slower growth. We show that over the entire reform period, from 1978-2018, China grew at 8.3% per annum, or 1.2 percentage points below the officially claimed 9.5% per annum. It nonetheless also implies that China’s accumulated real income over the past 40 years could be 36% smaller than we have presumed based on the official GDP data.
Editor’s note: The main research on which this column is based (Wu and Li, 2021) first appeared as a Discussion Paper of the Research Institute of Economy, Trade and Industry (RIETI) of Japan.
References
David, P (1966), “Measuring real net output: A proposed index”, The Review of Economics and Statistics 48(4): 419-425.
European Communities (2008), “Eurostat manual of supply, use and input-output tables”, Eurostat Methodologies and Working Papers, Luxembourg: Office for Official Publications of the European Communities.
Field, R M (1992), “China’s industrial performance since 1978”, The China Quarterly 131: 577-607.
Hulten, C R (1973), “Divisia index numbers”, Econometrica 41: 1017-1025.
Maddison, A (1998), Chinese economic performance in the long run, Organisation for Economic Cooperation and Development publishing, Paris.
Maddison, A and H X Wu (2008), “Measuring China’s economic performance”, World Economics 9 (2), April-June.
National Bureau of Statistics of China (2019), China statistical yearbook, China Statistics Press, Beijing.
OECD (2001), Measuring productivity: Measurement of aggregate and industry-level productivity growth, OECD Publishing, Paris.
Rawski, T G (1993), “How fast has the Chinese industry grown?”, World Bank Policy Research Working Paper 1194.
Sato, K (1976), “The meaning and measurement of the real value-added index”, The Review of Economics and Statistics 58(4): 434-442.
United Nations (2009), System of National Accounts 2008, New York.
Woo, W T (1996), “Chinese economic growth: Sources and prospects”, paper presented at Economics Discipline Seminar, RSPAS, Australian National University.
Wu, H X (2013), “How fast has Chinese industry grown? The upward bias hypothesis revisited”, China Economic Journal 6 (2-3): 80-102.
Wu, H X and K Ito (2015), “Reconstruction of China’s national output and income accounts and supply-use and input-output accounts in time series”, RIETI Discussion Papers 15-E-004.
Wu, H X and Z Li (2021), “Reassessing China’s GDP growth performance: An exploration of the underestimated price effect”, RIETI Discussion Papers 21-E-018.