Although the benefits of foreign direct investment (FDI) are well established in the economic literature, there remains a dearth of analysis of its impact within the European integration experience. Inward FDI is a major contributor to the diffusion of managerial best practices (Bloom et al 2012). It increases competition and shores up technological innovation (Alfaro et al 2004, Dhingra et al 2016). Also it should be more resilient than other international capital flows. Yet the literature estimating the FDI premium from EU membership remains scarce. European integration may have played a significant role and we need to get a good grasp of its effects.
Another reason to examine this issue is the comparison between the trade and the FDI impact of deep economic integration, of which the European integration experience is a textbook example. Focusing exclusively on trade, Glick and Rose (2016) find that earlier estimates of the effect of currency unions vanish when estimated using modern econometric techniques. Most of these techniques became standard after they published their original paper (Glick and Rose 2002). We ask whether the use of modern econometric techniques eliminates the effects of EU membership on FDI. We find that it does not, au contraire.
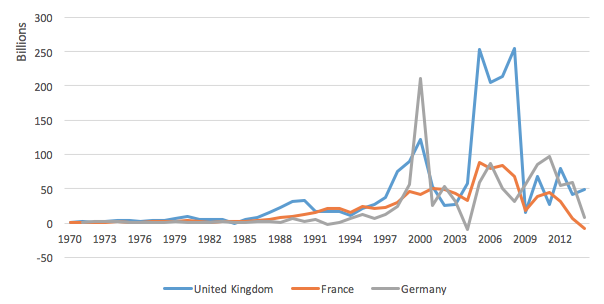
Figure 1 shows FDI net inflows for the three largest economies in the EU. The UK is by far the largest recipient. Net FDI inflows were small until the mid-1990s but exhibit two periods of rapid expansion – one in the second half of the 1990s and the other between the dot-com bubble and the financial crisis. It is also worth noting that these flows are much more volatile than expected, which may reflect the increasing share of more ‘footloose’ service activities, especially finance.
This column reports new estimates of the FDI premium from EU membership. We find that, between 1985 and 2013, EU membership increased FDI inflows by 28% (Bruno et al. 2016). This is a large, significant, and memorable effect – a percentage point for each of the 28 EU members. Our estimates for the FDI premium are robust and they range from 14% (Heckman) to 33% (OLS) to 38% (Poisson estimates). They survive the Glick-Rose critique and do so comfortably. However, and more importantly, they help advocate for FDI as a channel (in addition to trade) for delivering substantial payoffs from deep integration.
Figure 1. Foreign direct investment in France, Germany and the UK, 1970-2014
(net inflows, BoP, current US$)
Source: World Bank World Development Indicators 2015.
Estimating gravity
The gravity model has been a staple of international economics. It explains bilateral cross-border flows (trade, migration, investment, etc) based on the relative size and distance between countries or regions (Baldwin and Taglioni 2011, Head and Mayer 2014). A country’s economic size is expected to have a positive effect on bilateral flows while distance is expected to have a negative effect (distance is often taken to reflect a whole range of trade costs including language, bureaucracy, culture, etc). The last two decades have witnessed enormous progress in this area. Among many influential pieces, Anderson and van Wincoop (2003) and Santos Silva and Tenreyro (2006) are the crucial ones for our purposes. This new structural gravity approach (Fally 2015) provides needed theoretical underpinnings as well as strong support for the econometric estimation of gravity models.
In Bruno et al. (2016), we estimate the impact of EU membership on FDI. We used the latest available data on bilateral FDI flows, GDP and GDP per capita (sender and target), bilateral distance and the shares of manufacturing output, exports and imports in total GDP.
Our dataset covers 34 OECD countries between 1985 and 2013.1 Our data represent more than 70% of global FDI inflows and, because the countries are all OECD members, they are collected in a homogenous manner and are of relatively high quality. The main disadvantage of our data is the exclusion of developing countries including China and India.
The FDI premium from EU membership is 28%
We estimate the FDI premium from EU membership. Our modelling strategy follows the structural gravity approach. First, we estimate a baseline model using the natural logarithm of bilateral FDI flows; second, a Poisson model; and finally, a Heckman model that takes into account the zero bilateral trade flows and as such has a larger number of observations.2 In all cases, we control for dyadic fixed effects and time dummies.
We used the Heckman selection model to try to deal with whether we should treat all zero FDI in a special way. This is not a common approach in this literature, but it provides one additional robustness check because it should bias the estimated coefficients downwards. The likelihood of non-zero flows is modelled as a function of manufacturing, exports and import shares, and per capita GDP of the destination country. The selection equation generates some interesting lessons – a higher likelihood of positive FDI flows is related to lower per capita GDP in the destination country (FDI goes to countries where the return to capital is higher), higher industry shares (better integration in the value chain), lower export shares (substitution effect) and higher import shares of the target. The lambda term is significant and negative, suggesting that the error terms in the selection and primary equations are negatively correlated and the selection equation is needed.
Our dependent variable is bilateral FDI flows. The regressors in all specifications (OLS, Poisson, and Heckman) carry the expected signs. The size of the two countries (measured by GDP) and the level of development (GDP per capita) of the sender exert a positive effect on FDI flows (Bruno et al. 2016).
The main variable of interest for our present purposes is that capturing the effect of EU membership on FDI inflows. Focusing on the estimated coefficients for the EU target dummy for the host economy is between 14% and 38% depending on the estimator. This coefficient is always statistically significant. On the baseline OLS estimate the effect is 33% (= e0.285-1). In the Poisson model it is 38% (= e0.32 - 1). Using Heckman, which tries to control for selection on the zeros, the effect is 14% (= e0.13- 1) (for details, see Bruno et al. 2016).
A simple average of these three estimates would be 28% and we consider this to be the ‘baseline case’. In our view, this is a conservative estimate. If one takes the Glick and Rose critique seriously (and who can’t?), the econometrically appropriate average should be calculated either giving greater weight to the Poisson estimates or by severely downplaying the Heckman estimates (which is a method seldom used in this literature). Either way, a less conservative but more econometrically sensible estimate of the FDI premium from EU membership would put it at about 33%. This implies that FDI inflows are a third higher because the recipient country is a member of the EU.
How robust is our estimate of a 28% FDI premium from EU membership?
We have subjected our estimates to a wide range of robustness checks. First, we are implicitly treating the counterfactual to EU membership as simply being a standard member of the WTO, whereas we may believe being in the European Free Trade Association (EFTA) or the European Economic Area (EEA) is a more realistic alternative. If we add two dummy variables for being an EFTA sender or receiver, both coefficients are statistically insignificant and the EU recipient dummy remains positive and significant (0.211 with a standard error of 0.100). This suggests that it is being in the EU that matters. Further, the point estimate on being an EFTA recipient is actually negative (-0.206 with a standard error of 0.144). This implies that there may be some trade diversion from EFTA members like Switzerland to EU members (for example, because Switzerland is not in the single market for financial services). Second, we have focused on modelling flows, but an alternative would be to use FDI stocks. This gives qualitatively similar results. The EU recipient dummy always attracts a positive coefficient in the three alternative estimators in the equivalent to the results above. Third, we examine some of the dynamic impacts of EU membership. We find that the big effects came quite quickly following membership rather than taking a long time to feed through.
How does our 28% estimate compare with and relate to other estimates in the literature? Straathof et al. (2008) use a gravity model to examine bilateral FDI stocks. One of their specifications uses dyadic fixed effects, a somewhat different set of controls and earlier data (1981-2005). They find that EU membership yields a 28% increase in its inward FDI stocks from other EU countries and a 14% increase from non-EU countries (their Table 5.1, column 2). Bevan and Estrin (2004) focus on the new EU member states and show that even the announcement of start of EU membership negotiations has a positive and significant effect on FDI inflows. We can also look at the bilateral trade flows literature for a comparison, but we need to bear in mind that we focus on bilateral FDI in our model. Baier et al. (2008) find that trade is increased by about 130% after 10 to 15 years of EU membership, while the similar impact of EFTA membership is about 35%. We find instead that EU membership increases FDI inflows by about 28% in a country that is a member of the EU, which may be because trade is easier to adjust than FDI flows. This may help further our understanding of how benefits from deep integration actually take root (Campos et al. 2015).
Conclusions
How much additional FDI does a country receive as a consequence of being a member of the EU? This is obviously an important question for which, surprisingly, one still finds very few answers. We find EU membership robustly increases net FDI inflows. Our three main estimates range between 14% and 38% depending on the choice of econometric technique. The average of these is 28%. This is a large, robust, significant, substantial, and memorable benefit – a percentage point for each of the 28 members of the EU. Moreover, this result has enormous implications for the European integration project and for countries, like the UK, that are currently considering substantial changes to the terms of their relationship with the EU.
References
Alfaro, L, A Chanda, S Kalemli-Ozcan and S Sayek (2004) “FDI and economic growth: The role of local financial markets”, Journal of International Economics, 64(1): 89-112.
Anderson, J and E van Wincoop (2003) “Gravity and gravitas: A solution to the border puzzle”, American Economic Review, 93(1): 170-92.
Baier, S, J Bergstrand, P Egger and P McLaughlin (2008) “Do economic integration agreements actually work? Issues in understanding the causes and consequences of growth in regionalism”, The World Economy, 461-497.
Baldwin, R and D Taglioni (2011) “Gravity chains: Estimating bilateral trade flows when parts and components trade is important”, NBER, Working Paper No 16672.
Bevan, A and S Estrin (2004) “The determinants of foreign direct investment into European transition economies”, Journal of Comparative Economics, 32(4): 775-787.
Bloom, N, R Sadun and J Van Reenen (2012) “Americans do IT better: US multinationals and the productivity miracle”, American Economic Review, 102(1): 167-201.
Bruno, R, N Campos, S Estrin and C Meng (2016) “Gravitating towards Europe: An econometric analysis of the FDI effects of EU membership”, CEP Technical Paper, Brexit Analysis No 3.
Campos, N, F Coricelli and L Moretti (2015) “European integration: Benefits of deep versus shallow integration,” VoxEE.org, June.
Dhingra, S, G Ottaviano, T Sampson and J Van Reenen (2016) “The impact of Brexit on foreign investment in the UK”, CEP Brexit Analysis No 3.
Fally, T (2015) “Structural gravity and fixed effects”, NBER, Working Paper No 21212, forthcoming in Journal of Industrial Economics.
Glick, R and A K Rose (2002) “Does a currency union affect trade? The time-series evidence”, European Economic Review, 46(6): 1125-51.
Glick, R and A K Rose (2016) “Currency unions and trade: A post-EMU mea culpa”, mimeo (previous version NBER Working Paper No 21535, 2015).
Head, K and T Mayer (2014) “Gravity equations: Workhorse, toolkit, and cookbook”, chapter 3 in G Gopinath, E Helpman and K Rogoff (eds), Handbook of International Economics vol 4: 131-95, Elsevier.
Santos Silva, J M C and S Tenreyro (2006) “The log of gravity”, Review of Economics and Statistics, 88(4): 641-58.
Straathof, S, G-J Linders, A Lejour and J Mohlmann (2008) “The internal market and the Dutch economy: Implications for trade and economic growth”, CPG Netherlands Document No 168.
Endnotes
[1] The 34 OECD countries included are Austria, Australia, Belgium, Canada, Chile, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hungary, Iceland, Ireland, Israel, Italy, Japan, Korea, Luxembourg, Mexico, Netherlands, Norway, New Zealand, Poland, Portugal, Slovakia, Slovenia, Spain, Sweden, Switzerland, Turkey, the UK and the US.
[2] The maximum theoretical number of observations is 34*33*29=32,538. For many countries, especially before the 1980s, bilateral FDI flows are in fact zero. The missing values for FDI in the data reflect these zeros. Missing observations are assigned zeros.