Knowing whether an economy is too slack or at risk of overheating is crucial for macroeconomic policy. Economists generally look at price inflation, GDP level relative to potential, and the unemployment rate to assess, this but each measure has issues as can be seen when looking at the current US economy coming out of the Covid-19 crisis.1 An increase in inflation, as experienced in 2021, can be a marker of an overheating economy, but inflation can also increase due to temporary disruptions such as supply chain issues. Assessing whether GDP is below or above potential is challenging as a crisis like Covid-19 also affects the productive potential of the economy. The unemployment rate is 3.6% as of March 2022, not yet lower than just before Covid-19 when the economy did not show signs of overheating.
In this column, we propose a very simple rule to assess whether the economy, or more precisely the labour market, is too tight or too slack: are there more job openings than there are unemployed workers? This simple rule has intuitive appeal. If somehow job seekers were to be matched to job openings, would there be excess job openings, suggesting an economy with a shortage of willing workers (i.e. an overly tight labour market), or would there be excess job seekers left, suggesting an economy with too few jobs (i.e. an overly slack labour market)? It turns out that this simple intuitive rule can also be justified using the modern matching model that economists use.2 This reconciles economic theory with the widely scrutinised job-seeker-per-job-opening statistic.3
The Beveridge curve
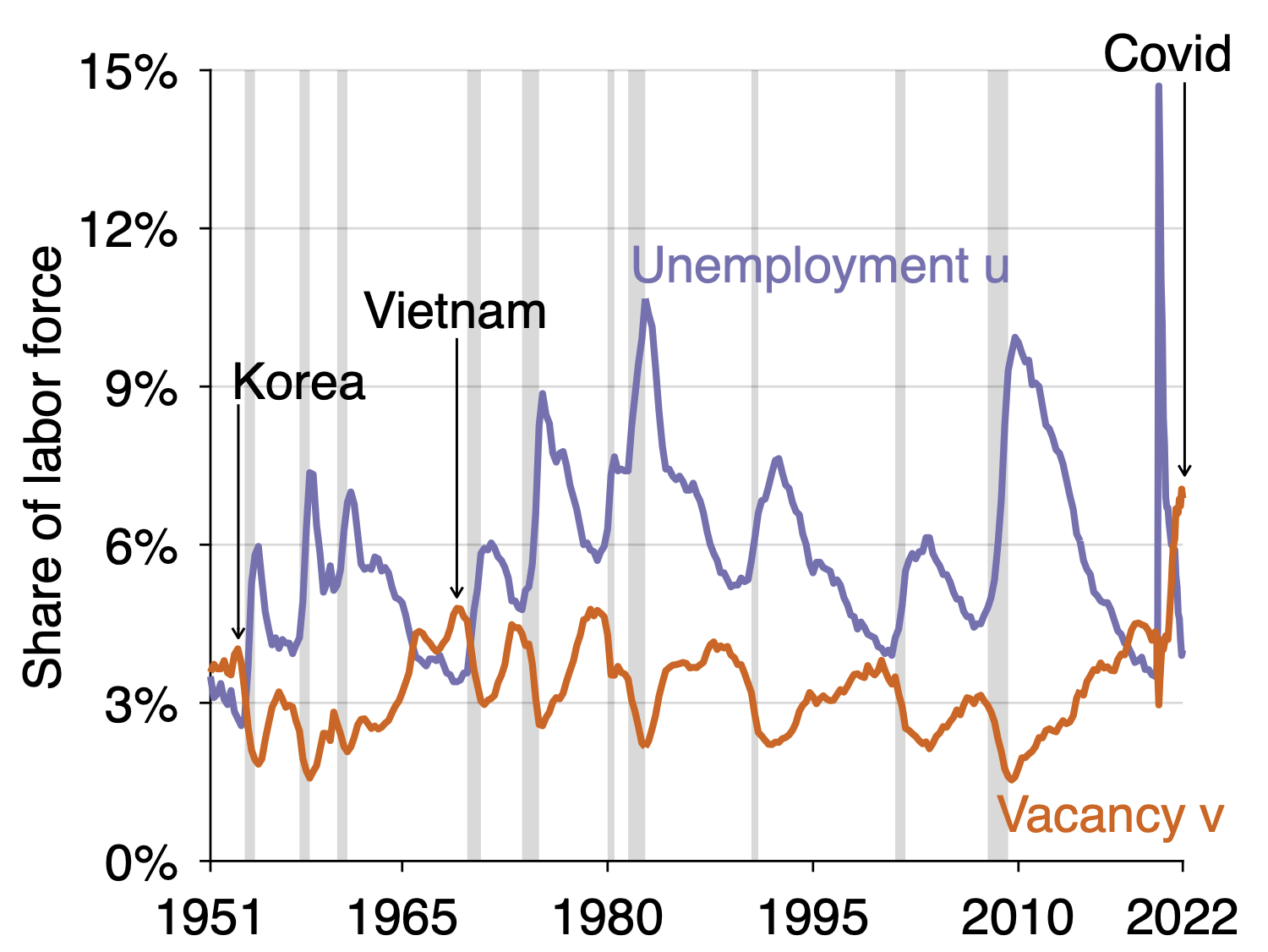
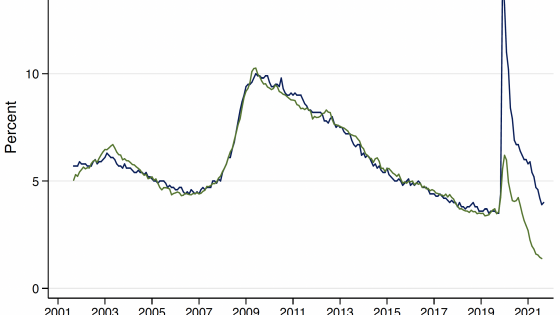
William Beveridge first noted in 1944 that the number of job openings and the number of job seekers in the UK move in opposite directions: When the economy is depressed, there are lots of job seekers and few job openings. Conversely, when the economy is booming, there are few job seekers and many job openings. This relationship has therefore been dubbed the ‘Beveridge curve’ and holds remarkably well in the US as well.4 Figure 1 depicts the time series of the unemployment rate u (all job seekers divided by the labour force which includes all workers and job seekers) and the vacancy rate v (all job openings divided by the same labour force) since 1951. The figure shows clearly that u and v move in opposite directions.
Figure 1 The US unemployment and vacancy rates since 1951
Note: This figure depicts the US unemployment rate and vacancy rate since 1951. The unemployment rate u is constructed by the Bureau of Labor Statistics as the number of active job seekers divided by the civilian labour force. The vacancy rate v is the number of job openings measured by the Bureau of Labor Statistics in the Job Opening and Labor Turnover Survey and also divided by the civilian labour force. The unemployment and vacancy rates move in opposite directions over the business cycle. The vacancy rate v exceeds the unemployment rate u only rarely. Since 1951, this happened in the early 1950s during the Korean War, the late 1960s during the Vietnam War, 2018-2019 just before Covid-19, and most prominently since mid-2021 coming out of the Covid-19 crisis.
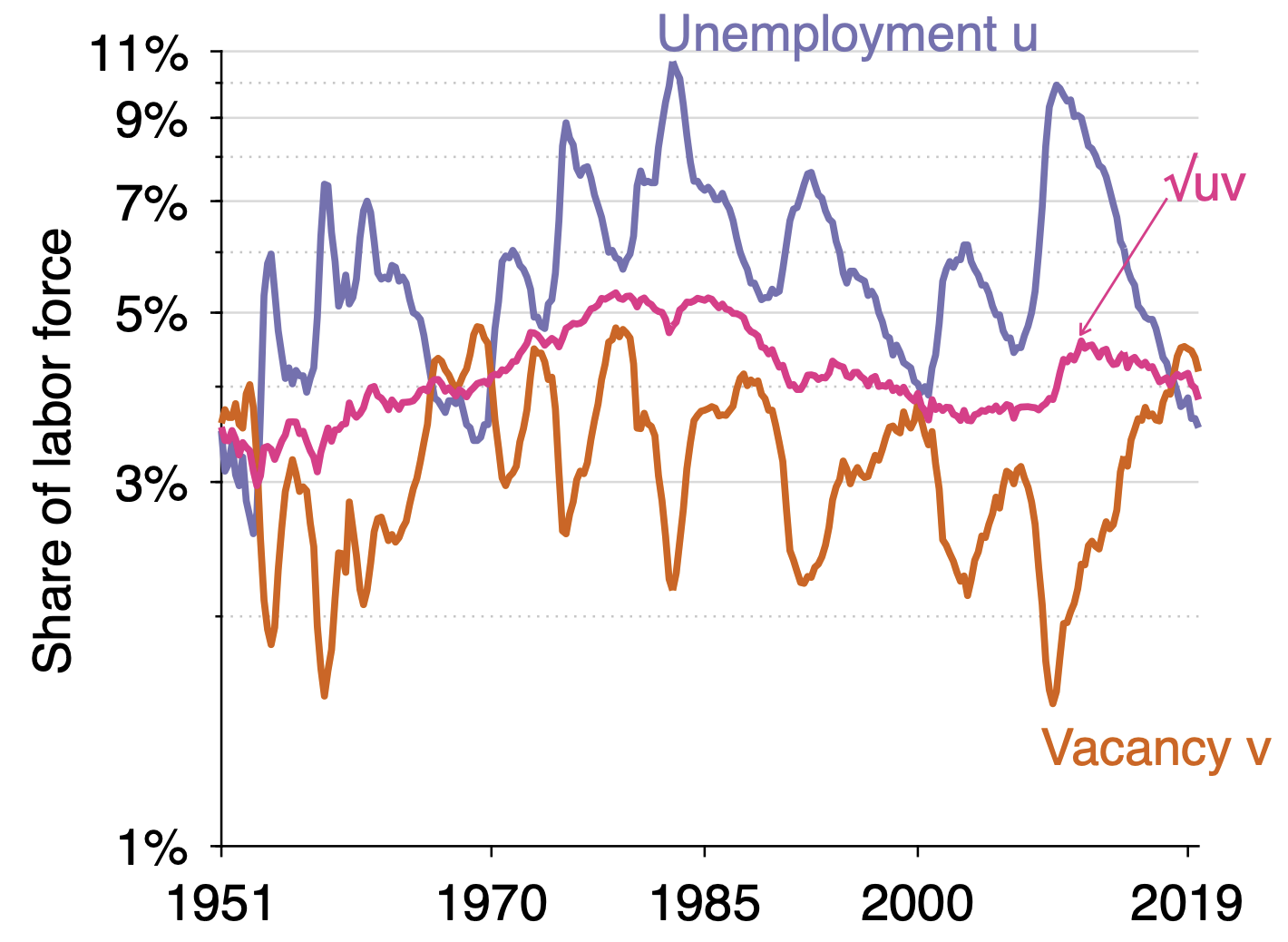
At any point in time, during good times or bad times, many workers quit their jobs or are laid off (separations) and many job seekers find jobs (new matches). Such gross flows dwarf net flows (the net increase or decrease in the total number of jobs). Therefore, new matches roughly equal separations. Every month in the US, about 4% of all jobs end up in a separation and a roughly equivalent number of new matches are created.5 New matches depend both on the number of job seekers and the number of job openings. Hence, if there are few job seekers, many job openings are needed to create all these new matches. Conversely, if there are many job seekers, fewer job openings are needed. Quantitatively, the unemployment rate u and the vacancy rate v are linked so that they are the inverse of each other, namely that doubling u cuts v in half and inversely.6 Indeed, Figure 2 displays again u and v but now in log-scale, and you can see that the movements up and down of u and v are almost like the mirror image of each other, looking like butterfly wings. Why is that? Empirically, the number of new matches depends symmetrically on the number of job seekers and job openings.7 Doubling job seekers increases new matches the same as doubling job openings. This makes intuitive sense as both job seekers and job openings are striving to find each other. This is obvious for job seekers who spend time looking for jobs, applying, doing interviews, but this is also the case for job openings where workers in the recruiting firm have to advertise job openings, screen, and interview applicants. Therefore, as new matches have to meet the level of job separations, cutting in half the number of job seekers requires doubling the number of job openings, explaining why u and v are the inverse of each other.
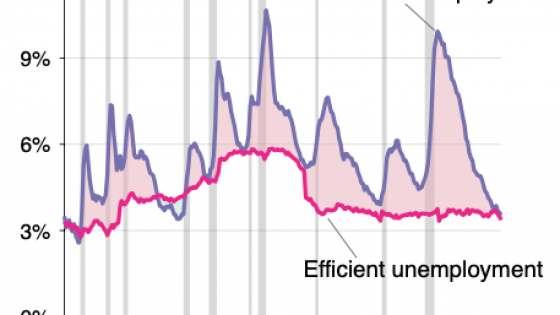
Figure 2 The efficient unemployment and vacancy rate in the US, 1951-2019
Note: This figure repeats Figure 1 but excluding the Covid-19 period and using a log-scale for the unemployment rate and the vacancy rate. The figure shows that the two statistics – log(u) and log(v) – are mirror images of each other. This is particularly striking at both statistics are constructed completely independently of each other. This symmetry implies a Beveridge curve where u and v are (almost exactly) inversely related (uv = constant). Minimising waste u + v subject to the Beveridge curve uv = constant implies u* = v* = √(uv). The time series of √(uv), this efficient unemployment and vacancy rate is depicted on the figure, it lies exactly in the middle of u and v (in log-scale). It is fairly constant over time and hovers between 3% and 5%. The actual unemployment rate is too high except in rare instances: 1951-1953 (Korean War), 1966-1969 (Vietnam War), 2018-2019 (just before the Covid-19 crisis).
Efficient unemployment
What is the ideal level of unemployment? Unemployment is clearly a waste of economic resources as people who would like to work and produce are not able to do so. Yet, contrary to naïve intuition, an almost zero unemployment rate is neither feasible nor desirable because, by the logic of the Beveridge curve, it would require a huge number of job openings. As we mentioned, servicing job openings takes work in the form of posting ads and screening and interviewing candidates – work that has to be diverted away from other productive tasks. Therefore, job openings also consume economic resources. It turns out that, on average, servicing one job posting requires the attention of one worker. Intuitively, it takes work for the job opening search to be active. Job recruiting is as labour-intensive as job seeking is. Machines cannot do recruiting for firms. Therefore, one job opening consumes about as much resources as what is wasted when one person is looking for a job instead of working.8
Ideally, we would like to minimise wasted resources from both unemployment and from servicing job openings. Because a job opening is as costly as a job seeker, this means minimising the sum of job seekers and job openings. Equivalently, this amounts to minimising the sum of the unemployment rate u and the vacancy rate v. We can’t set them both at zero because u and v are inversely related through the Beveridge curve. Minimising the sum of the unemployment rate and the vacancy rate knowing that these two rates are inversely related through the Beveridge curve has the simple symmetric solution that the optimal unemployment and vacancy rates u* and v* should be equal and both are given by the geometric average of the current unemployment rate u, and the current vacancy rate v.9 In other words, the number of job seekers should be equal to the number of job openings. If u exceeds v, the labour market is too slack, and reducing u and increasing v would reduce waste. If u is less than v, the labour market is too tight, and increasing u and reducing v would reduce waste.
We depict the efficient unemployment rate in Figure 2; it typically hovers between 3% and 5% since 1951. Most of the time, the unemployment rate is too high, and particularly so during recessions. The labour market is rarely too tight. Before Covid-19, this has happened only three times since 1951: 1951-1953, 1966-1969, 2018-2019. The 1951-1953 and 1966-1969 episodes correspond to the Korean and Vietnam Wars that sent many young men serving overseas and removed them from the civilian labour force, making the civilian job market tighter. The pre-Covid-19 boom also appears as a period where the labour market was slightly too tight according to our formula.
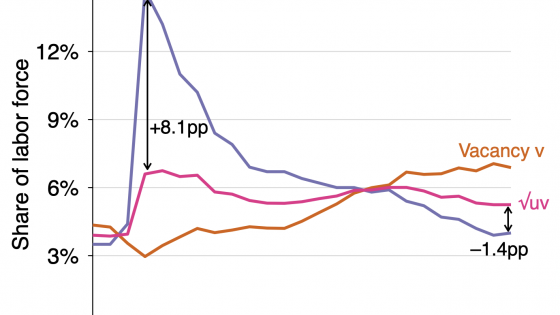
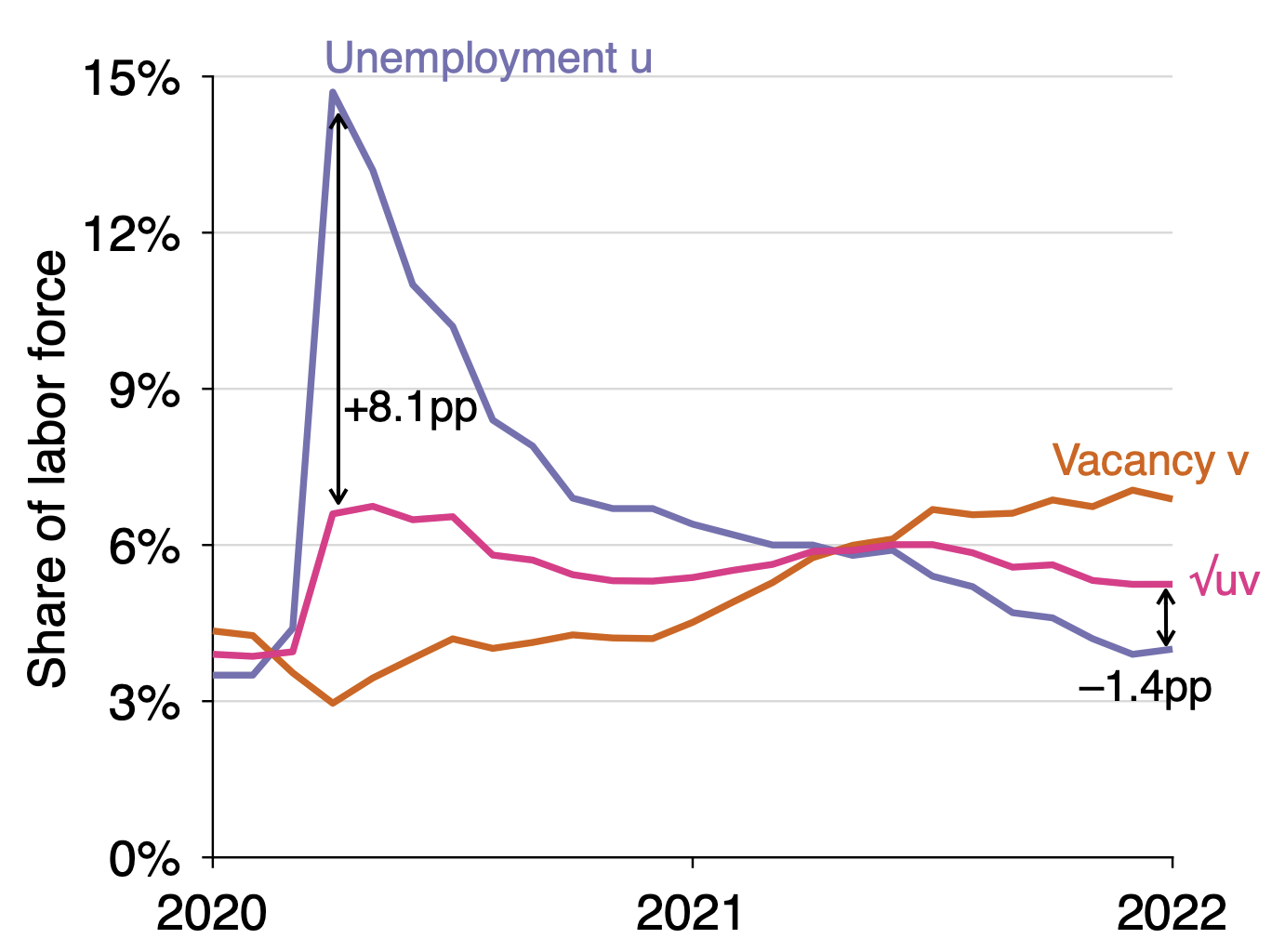
Figure 3 zooms in on the Covid-19 period. The unemployment rate shot up to almost 15% during Covid-19 which was the highest since 1951. However, the unemployment rate quickly dropped and the vacancy rate increased. Around May 2021, the u and v curves crossed at 6%. This is a time where the efficient unemployment rate is quite high (at 6%) because of the extraordinary disruptions of the Covid-19 crisis that shifted out the Beveridge curve. Since May 2021, the vacancy rate v exceeds the unemployment rate, implying that the labour market is too tight. In the last months of 2021 and early 2022, v has exceeded u by more than three points, which has never happened in the US over the last 70 years. Therefore, our analysis suggests that the labour market has become excessively tight in the second part of 2021 and that by 2022, the US labour market is at its tightest since at least 1951. We estimate that the current unemployment rate of 3.6% is about 1.5 percentage points below its efficient level, which is around 5%.
Figure 3 US unemployment and vacancy rates: Actual versus efficient during Covid-19
Note: This figure depicts the actual unemployment rate u and vacancy rate v monthly during the Covid-19 period from January 2020 to January 2022. It also depicts the efficient unemployment rate u* and vacancy rate v* given by the formula u* = v* = √(uv). Early in the Covid-19 crisis, the unemployment rate was 8.1 percentage points above its efficient level, the worst unemployment gap since 1951 (see Figure 2). However, this gap has closed quickly and since May 2021, the vacancy rate v exceeds the unemployment rate implying that the labour market has become too tight. In January 2022, actual unemployment is 1.4 percentage points below its efficient level. The unemployment rate has never been so much below its efficient level since 1951 (see Figure 2). This suggests that in early 2022, the US economy is experiencing its tightest labour market since 1951.
References
Blanchard, O and P Diamond (1989), “The Beveridge Curve”, Brookings Papers in Economic Activity 20(1): 1–76.
Domash, A and L H Summers (2022), “Overheating conditions indicate high probability of a US recession”, VoxEU.org, 13 April.
Elsby, M W L, R Michaels and D Ratner (2015), “The Beveridge Curve: A Survey”, Journal of Economic Literature 53(3): 571–630.
Hosios, A J (1990), “On the Efficiency of Matching and Related Models of Search and Unemployment”, Review of Economic Studies 57(2): 279–298.
Michaillat, P and E Saez (2020), “Keeping track of the unemployment gap”, VoxEU.org, 12 April.
Michaillat, P and E Saez (2021), “Beveridgean Unemployment Gap”, Journal of Public Economics Plus 2, 100009.
Petrongolo, B and C A Pissarides (2001), “Looking into the Black Box: A Survey of the Matching Function”, Journal of Economic Literature 39(2): 390–431.
Pissarides, C A (2000), Equilibrium Unemployment Theory, 2nd edition Cambridge, MA: MIT Press.
Villena-Roldan, B (2010), “Aggregate Implications of Employer Search and Recruiting Selection”, CEA Working Paper 271.
Endnotes
1 The VoxEU column by Domash and Summers (2022) provides a recent stimulative discussion.
2 A more detailed and general presentation is proposed in Michaillat and Saez (2021) and summarised in Michaillat and Saez (2020).
3 https://www.bls.gov/charts/job-openings-and-labor-turnover/unemp-per-job-opening.htm
4 The classical study of the US Beveridge Curve is Blanchard and Diamond (1989).
5 See https://fred.stlouisfed.org/series/JTSTSR
6 Mathematically, u times v is approximately constant.
7 Technically, the matching function in the US appears to follow a Cobb-Douglas form with exponents of 0.5 on unemployment and vacancies (see Michaillat and Saez (2021, p. 9) for a survey of the US estimates based on aggregate data, and Petrongolo and Pissarides (2001) for a broader survey).
8 The cost of recruiting can be measured from the National Employer Survey, which was conducted by the Census Bureau in 1997 (Villena Roldan 2010). Michaillat and Saez (2021, p. 11) estimates that servicing a vacancy requires 0.92 (i.e. almost 1) worker at any point in time.
9 Mathematically, min u + v subject to uv = C implies that u* = v* = √C = √uv.