How a firm grows is one of the important themes in the industrial organisation literature and has been discussed extensively. An influential paper is the seminal work by Gibrat (1931), which continues to receive much attention in the theoretical and empirical literature (for a review, see Sutton 1997). If the growth rate of a firm is defined as the difference in the logarithm of the firm’s size, Gibrat’s model is described by the following assumptions:
- The growth rate of a firm is independent of its size.
- The successive growth rates of a firm are independent of each other.
- The growth rate of a firm consists of small shocks that satisfy the conditions of the standard central limit theorem (CLT).
In his model, firm growth is considered as the consequence of an accumulation of many small shocks. By the central limit theorem, the model predicts that the distribution of growth rates becomes Gaussian.
In the literature, a large number of studies have been devoted to test the validity of assumptions 1 and 2 (see Santarelli et al. 2006 for a review). Although the results are inconclusive—which is why many economists continue to test Gibrat’s model empirically more than 80 years after its publication—they seem to suggest that assumptions 1 and 2 can be taken as a good starting point. However, recent studies show that the empirical distribution of growth rates of firms is not Gaussian.
Laplace distribution and jump processes
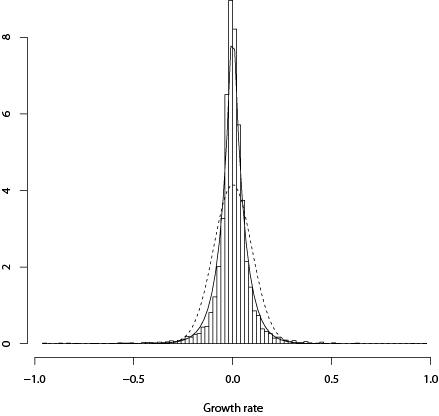
Since Stanley et al. (1996), subsequent papers have confirmed that the distribution of firm growth rates is not Gaussian; rather, it closely follows the Laplace distribution. See Figure 1 for Japanese firms. The Laplace distribution has a fatter tail than the Gaussian, namely, there is a relatively higher probability that a firm experiences more extreme events than predicted by a Gaussian distribution. The non-normality of growth rates challenges the existing models based on Gibrat because it indicates the underlying mechanism of firm growth is different from the one suggested by Gibrat’s model. More interestingly, the same characteristics of firms’ growth rate distributions appear at the finer sectoral level. This is a robust feature that holds at various levels of aggregation. Obviously, it is important to investigate why Gibrat’s model fails and which assumption of the model is violated. As discussed above, assumptions 1 and 2 are supported by empirical data whereas assumption 3 is not.
Figure 1. Histogram of the growth rate of Japanese firms. The solid (dotted) curve is the Laplace (Gaussian) distribution.
In Arata (2014), we assume that the growth rate consists of independent random shocks but does not satisfy the conditions of the standard central limit theorem. A firm grows for all sorts of reasons, for example, the introduction of new products, quality improvement of existing products, cost reduction induced by technological progress, creation of new markets, and effective advertisement. On the other hand, firm size can also decrease, for example, due to competition with other firms, serious conflicts with a labour union, change of consumer preferences, and emergence of superior substitutes for the firm’s product. It is plausible to assume that these shocks are different in terms of their impacts on the firm’s performance. Some shocks are expected to have a disproportionate impact on the firms. Therefore, we need a broad generalisation of the standard central limit theorem.
A fundamental limit theorem on sums of independent random variables was given by Khintchine (1937). The theorem states that if the distribution of sums converges, its limit belongs to infinitely divisible distributions. This family of distributions includes the Laplace distribution, as well as the Gaussian. Moreover, if an infinitely divisible distribution is given, there exists a corresponding Levy process. The Levy process corresponding to the Laplace distribution is called variance gamma process. Therefore, the sample path properties of this process represent how a firm grows. One can find that this process is a pure jump process, that is, its value increases or decreases by jumps (see Figure 2).
Figure 2. An example of jump processes; the process increases its value by jumps.
This is in sharp contrast to the Brownian motion, which is predicted by Gibrat’s model. Because the Brownian motion has only a continuous part, only small continuous movements exist in Gibrat’s model. On the contrary, the firm growth dynamics in our model are characterised by discrete movements, that is, jumps. If we collect a small number of such large jumps (e.g., successful innovations), that would largely explain the firm’s growth.
Using data on publicly traded Japanese companies, we can estimate the structure of the jumps. For example, a positive growth shock larger than 3%, on average, occurs once every two years. In the case of an 8% growth shock, on average, it occurs once every 10 years. Note that these jumps are comparable to annual growth rates. That is, the growth of firms is largely determined by these large jumps.
Conclusion
Our analysis is also related to radical innovation in the literature on innovation management. Radical innovations involve the development or application of something fundamentally new that creates a wholly new industry or causes a complete transformation of the market structure. In our model, the radical innovations correspond to large jumps. Radical innovations are critical to the long-term growth of firms and differ significantly from incremental innovation (see, for example, Leifer et al. 2000). Firms that dominate the existing market but lag behind in competition for radical innovation often fail to maintain their leading positions Small firms that engage and succeed in radical innovation usually bring down giants and gain the leading position in the market. Thus, radical innovation (or large jumps) is a key element in the long-term success of a firm. The observed Laplace distribution of growth rates clearly represents these phenomena. A small number of successful innovations leads to the rapid expansion of a firm.
Moreover, radical innovation is an engine of economic growth. It revolutionises existing markets or opens up whole new industries. As Schumpeter (1942) states, “Creative destruction is the essential fact about capitalism.” Therefore, investigating the statistics of growth rates has an important meaning in macroeconomics as well as firm growth theory.
Editor's note: The main research on which this column is based (Arata 2014) first appeared as a Discussion Paper of the Research Institute of Economy, Trade and Industry (RIETI) of Japan.
References
Arata, Y (2014), “Firm Growth Dynamics: The importance of large jumps”, RIETI Discussion Paper Series 14-E-033.
Gibrat, R (1931), Les Inegalites Economiques, Recueil Sirey.
Khintchine, A (1937), “Zur theorie der unbeschrankt teilbaren Verteilungsgesetze,” Mat Sbornik 2 (44), 1.
Leifer, R, C McDermott, G C O’Connor, L Peters, M Rice, R Veryzer (2000), Radical Innovation: How Mature Firms Can Outsmart Upstarts, Boston: Harvard Business School Press.
Santarelli, E, L Klomp, A Thurik (2006), “Gibrat’s Law: An Overview of the Empirical Literature,” In: Santarelli, E. (Ed.), Entrepreneurship, Growth, and Innovation; Vol. 12 of International Studies in Entrepreneurship, Springer US, pp. 41–73.
Schumpeter, J A (1942), Capitalism, Socialism and Democracy, New York: George Allen & Unwin.
Stanley, M H, Amaral, L A, Buldyrev, S V (1996), “Scaling behaviour in the growth of companies”, Nature 379 (6568), 804–806.
Sutton, J (1997), “Gibrat’s Legacy”, Journal of Economic Literature 35 (1), pp. 40–59.