Even before the euro crisis started, it had been widely argued that the Eurozone needed a mechanism to help countries overcome idiosyncratic shocks. The experience of the crisis itself seemed to make this case overwhelming, and throughout the EU institutions it is now taken for granted that the Eurozone needs a system of fiscal shock absorbers. For example, The Report of the President of the European Council calls for:
“Stage 3 (post 2014): establish a well-defined and limited fiscal capacity to improve shock absorption capacities, through an insurance system set up at the central level…”
Following this line of thought, a number of shock absorber mechanisms have been proposed recently. These mechanisms usually stipulate that a certain percentage of each upswing or downturn in the economy should be offset by payments to a central fund (see Dullien 2013 or Enderlein 2013, for example). But this approach neglects a key insight from the economics of insurance.
Insurance and convexity
Insurance is useful when the cost of unpredictable events is convex – when a shock of twice the magnitude of another one causes more than twice as much damage. The standard case for insurance at the microeconomic level is simply that utility functions are assumed to be concave (and hence the cost of losing income convex). The euro crisis has vividly illustrated that the costs of large shocks can be more than proportionally large, especially when a shock impairs access to financial markets. In this case consumption smoothing is no longer possible, or very expensive. The case of Greece has also shown that the social cost of very large, ‘catastrophic’ shocks can be extremely severe, because a shock which leads to insolvency creates other problems, including widespread bankruptcy costs. By contrast, the small shocks that were prevalent during the ‘Great Moderation’ did not involve large costs, as temporary shocks to output or income can be smoothed at a low cost via savings or borrowing in the capital market.1
There are thus good reasons why social loss functions are assumed to be convex. Most optimal control models simply assume a special form of convexity, namely that the social loss function is quadratic in output (or output compared to its equilibrium level – see Blanchard and Fischer 1989).2
Insurance with deductible first best
A widespread practice in the insurance industry is to offer clients full coverage only above a certain deductible or threshold. This approach should be applied to the discussion about the need for a shock absorber for the Eurozone as well.
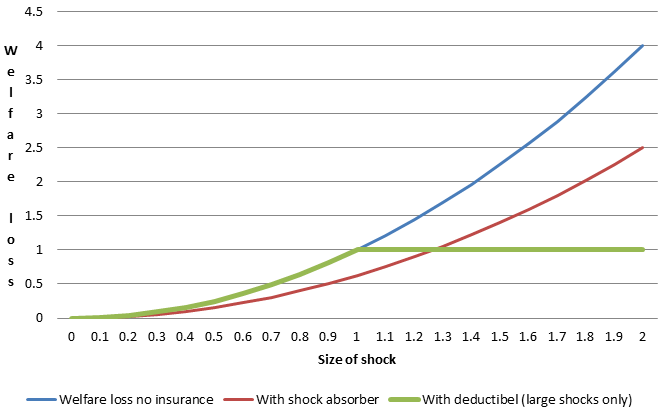
The basic idea behind insurance with a deductible can be illustrated easily: Figure 1 below shows the usual quadratic social loss function (blue lines) as the square of the shock which is hitting the economy (e.g. the increase in unemployment or the fall in GDP) on the horizontal axis. This is what the economy would be subject to in the absence of an insurance mechanism.
With a (partial) shock absorber which offsets a certain percentage of the shock (as proposed by Enderlein 2013), the welfare impact of all shocks is lower, as indicated by the red line.
An alternative to a shock absorber is to introduce a deductible, but to fully compensate all shocks above that threshold. The resulting welfare loss as a function of the shock is indicated by the green line (where the threshold was set at 1).
The actuarially fair price for both insurance policies will of course depend on the parameters of the probability density function of the shocks, the percentage of the shock absorbed, and the deductible.
In Figure 1 below, the difference between the welfare losses under the two approaches can be determined as the difference between the areas between the green and the red lines to the left and to the right of the point where they meet. The example drawn here suggests that the area to the right is much larger, but the two areas must be weighted by the probability of these shocks occurring. It thus seems that a priori it is not possible to say whether a shock absorber or an insurance contract with a deductible is superior.3
However, there exists a general theorem that insurance with a deductible is superior. Arrow (1974) proved that “if we stay within the class of contracts with the same expected loss, EU [expected utility] maximizers prefer a contract with full (100%) insurance above a fixed deductible.”4
Figure 1. Welfare loss with a (partial) shock absorber vs insurance with deductible
Source: own calculations.
An illustration: Normally distributed shocks
The advantage of insurance with a deductible over a shock absorber (with the same premium) can be illustrated graphically using the most widely used functional form concerning the distribution of the shocks, namely that they are normally distributed. This is often a convenient assumption to solve linear quadratic problems, but has the disadvantage that, for the normal (Gaussian) distribution (or probability density function) of the shock, one can only calculate numerically the truncated variances and expected values that one needs to evaluate the welfare losses and the actuarially fair cost of providing either a shock absorber or insurance with a deductible.5
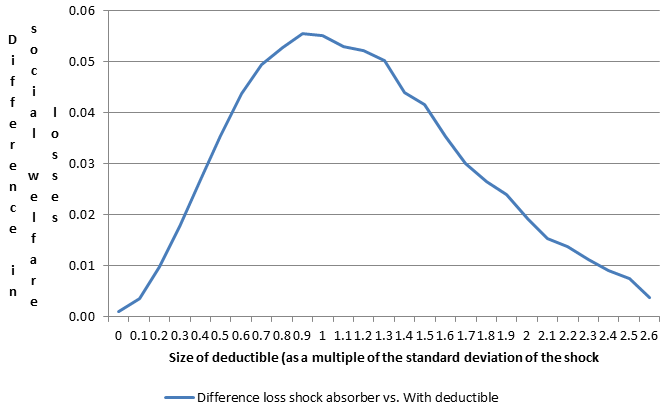
Figure 2 below thus shows the difference between the welfare loss under a shock absorber and insurance with a deductible as a function of the deductible in terms of the standard deviation of the distribution of the shock. The size of the shock absorber was in all cases adjusted so that the actuarially fair price of both contracts was the same.
It is apparent that in Figure 2 the difference is always positive, i.e. the welfare loss is always lower under an insurance contract with a deductible, as proven more generally by Arrow (1974).
Figure 2 shows also a general property of insurance with a deductible. The value of such an insurance contract depends on the size of the deductible: if it is zero the contract provides full insurance; whereas if the deductible is infinity there is no insurance at all. This also implies that the difference between a shock absorber and insurance with a deductible must go towards zero as the deductible goes to zero (in this case the shocks absorber will have to go to full shock absorption); and it must also go to zero as the deductible goes towards infinity, since at that point there will be little difference between the two types of insurance.
Figure 2 below refers to the case of the shock having a standardised Gaussian distribution. In this case the difference reaches a maximum if the deductible is equal to one (one standard deviation). In other words, a deductible equal to one standard deviation of the shock provides the situation where the advantage of this type of contract is largest.
Figure 2. Difference between social losses shock absorber vs insurance with deductible
Source: own calculations, based on data provided by Claudius Gros
Conclusions
Many observers and policymakers now argue that the Eurozone needs a system of fiscal shock absorbers like that of the US.
A recent study by the IMF (2013a and 2013b) finds that about 20% of shocks to state income are offset by the US federal fiscal system. But such a system would have been of limited value in the euro crisis. Offering a country whose output falls by 1% (relative to the Eurozone average) a transfer of 0.2% of GDP would be of very limited usefulness. A country hit by a very large shock, say 5% of GDP (like Portugal or Ireland) would of course receive a larger transfer, but the problems would not be substantially different (a fall of income by 4% instead of 5%). By contrast, in a system of insurance with a deductible, of say 1% of GDP, the country hit by a small shock would receive nothing. But most of the large shock – everything above the 1% deductible – could then be offset.
What the Eurozone really needs is not a system which offsets all shocks by some small fraction, but a system which protects against shocks which are rare, but potentially catastrophic. The many minor cyclical shocks which do not impair the functioning of financial markets can then be dealt with via borrowing at the national level.
The European Stability Mechanism – the Eurozone’s rescue mechanism – does not provide the needed insurance function because it only provides loans, which have to be repaid with interest, rather than a transfer when a shock materialises. One way to create an insurance mechanism with a deductible would be to create a system of reinsurance for national unemployment insurance systems, under which the national systems would pay regular premiums to a central Eurozone fund. This fund would then support the national system in countries where the unemployment rate has increased suddenly above a certain threshold. This is the type of absorption capacity that the Presidents of the EU should be considering – not merely copies of the way the US federal fiscal system appears to offset a small proportion of all shocks.
References
Arrow, K (1974), “Optimal Insurance and Generalized Deductibles”, Scandinavian Actuarial Journal, 1974(1): 1–42.
Asdrubali, Pierfederico, Bent E Sorensen, and Oved Yosha (1996), “Channels of Interstate Risk Sharing: US 1963–90”, Quarterly Journal of Economics, 111(4): 1081–1110.
Benigno, P P and Michael Woodford (2004), “Optimal monetary and fiscal policy: a linear-quadratic approach”, ECB Working Paper 345.
Blanchard, O and S Fischer (1989), Lectures on Macroeconomics, MIT Press, Chapter 11.
Dullien, Sebastian (2013), “A Common Unemployment Insurance System for the Euro Area”, DIW Economic Bulletin, 3(1).
Enderlein, H, L Guttenberg, and J Spiess (2013), “Making One Size Fit All – Designing a Cyclical Adjustment Insurance Fund for the Eurozone”, Notre Europe Policy Paper 61.
Furceri, D and A Zdzienicka (2013), “The Eurozone Crisis: Need for a Supranational Fiscal Risk Sharing Mechanism”, IMF Working Paper 13/198.
Gollier, C and H Schlesinger (1996), “Arrow’s Theorem on the Optimality of Deductibles: A Stochastic Dominance Approach”, Economic Theory, 7: 359–363.
IMF (2013a), “Toward a Fiscal Union for the Euro Area”, prepared by Céline Allard, Petya Koeva Brooks, John C Bluedorn, Fabian Bornhorst, Katharine Christopherson, Franziska Ohnsorge, Tigran Poghosyan, and an IMF Staff Team.
IMF (2013b) “Toward a Fiscal Union for the Euro Area: Technical Background Notes”, September.
Mayer, Thomas (2002), “The Macroeconomic Loss Function: A Critical Note”, CESifo Working Paper 771.
Russell, Thomas (2004), “Catastrophe Insurance and the Demand for Deductibles”, manuscript, Santa Clara University Department of Economics.
1 There is some confusion in the literature on the purpose of shock absorbers. In principle, the ultimate motive for insurance should be to smooth consumption over time. But most empirical analysis concentrates on the variability of income (GDP). Asdrubali et al. (1996) are among the few to analyse how variations in income are transmitted to variations in consumption. Furcieri and Zdzienicka (2013) build their proposal on this approach.
2 Benigno and Woodford (2004) derive this functional form somewhat more generally. For a critique, see Mayer (2002).
3 Formally, the cost of a shock absorber under which a fraction alpha of any shock, x, is absorbed by the insurer is given by alpha*E(x). If welfare losses are a quadratic function of the shock, one can calculate the following expected losses:
1) No shock absorber. In this case the welfare loss would be proportional to the variance of the shock, i.e. E(x2).
2) Shock absorber: In this case the welfare loss would be proportional to the variance of the shock attenuated by the fraction alpha, or (1-alpha)2*E(x2).
3) Insurance with deductible: In this case the welfare loss would be given by the sum of two elements: For a shock smaller than the deductible (indicated by gamma) one has to take the expected value of x2, but for larger shocks (i.e. x>gamma) the welfare loss will be just equal to gamma2 (which has to be multiplied by the probability that x>gamma).
4 See Russel (2004). See also Gollier and Schlesinger (1996) for a more general version of the theorem about the optimality of full insurance above some fixed deductible.
5 Another drawback of the normal distribution is that reality has ‘fat tails’ – large events occur more often than one would expect if the distribution were normal.