This year marks the 60th anniversary of the workhorse model of trade – the gravity equation (Tinbergen1962). Gravity is a ‘celebrity’ among economic models; it has been applied and extended in thousands of papers by trade economists, colleagues from other fields, and policy practitioners. Moreover, as noted by the brilliant late Peter Neary, the gravity equation is probably the only econometric model that has been featured on the front page of the Financial Times (on 19 April 2016).
Unfortunately, and as sometimes happens to celebrities, the gravity model is misspecified (misunderstood) by the press. More worrisome, we often see gravity applications in academic papers and policy reports that are not consistent with theory and/or do not take into account major developments in the empirical gravity literature. As a result, the estimates in such papers could be severely biased and their policy recommendations could be misleading. Moreover, while it is well understood that trade theory and trade-policy analysis should be set in general equilibrium (GE), there is still a division and scepticism among academics and trade-policy practitioners about the usefulness of the gravity as a Computable GE (CGE) framework for counterfactual projections. A prominent example, which motivated the inclusion of the gravity equation in the Financial Times, is the debate among UK economists over gravity-based projections of the Brexit effects.
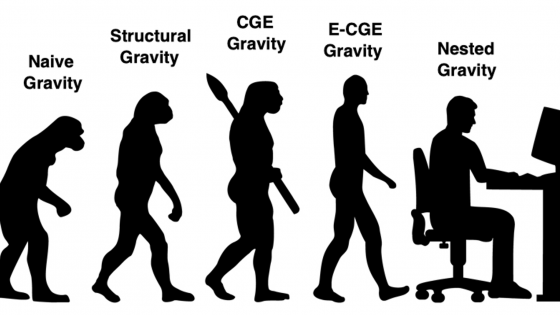
To celebrate gravity’s anniversary and address some misconceptions about the gravity model, in a new paper (Yotov 2022) I trace its evolution, as depicted in Figure 1, from a naive application to an ‘estimating CGE’ (E-CGE) model that can be nested in more complex frameworks.
Figure 1 Evolution of the gravity model of trade
An important reason for the popularity of gravity is that, by analogy with physics:
Gravity is very intuitive.
Just like Newton's law of universal gravitation, the gravity equation of trade implies that trade (the gravitational force) between two countries (two objects) is directly proportional to the product of their sizes (masses) and inversely proportional to the trade frictions (the square of distance) between them. In other words, the larger and the closer two countries are, the more they trade with each other. What makes this analogy even more impressive is that:
Gravity has solid theoretical foundations.
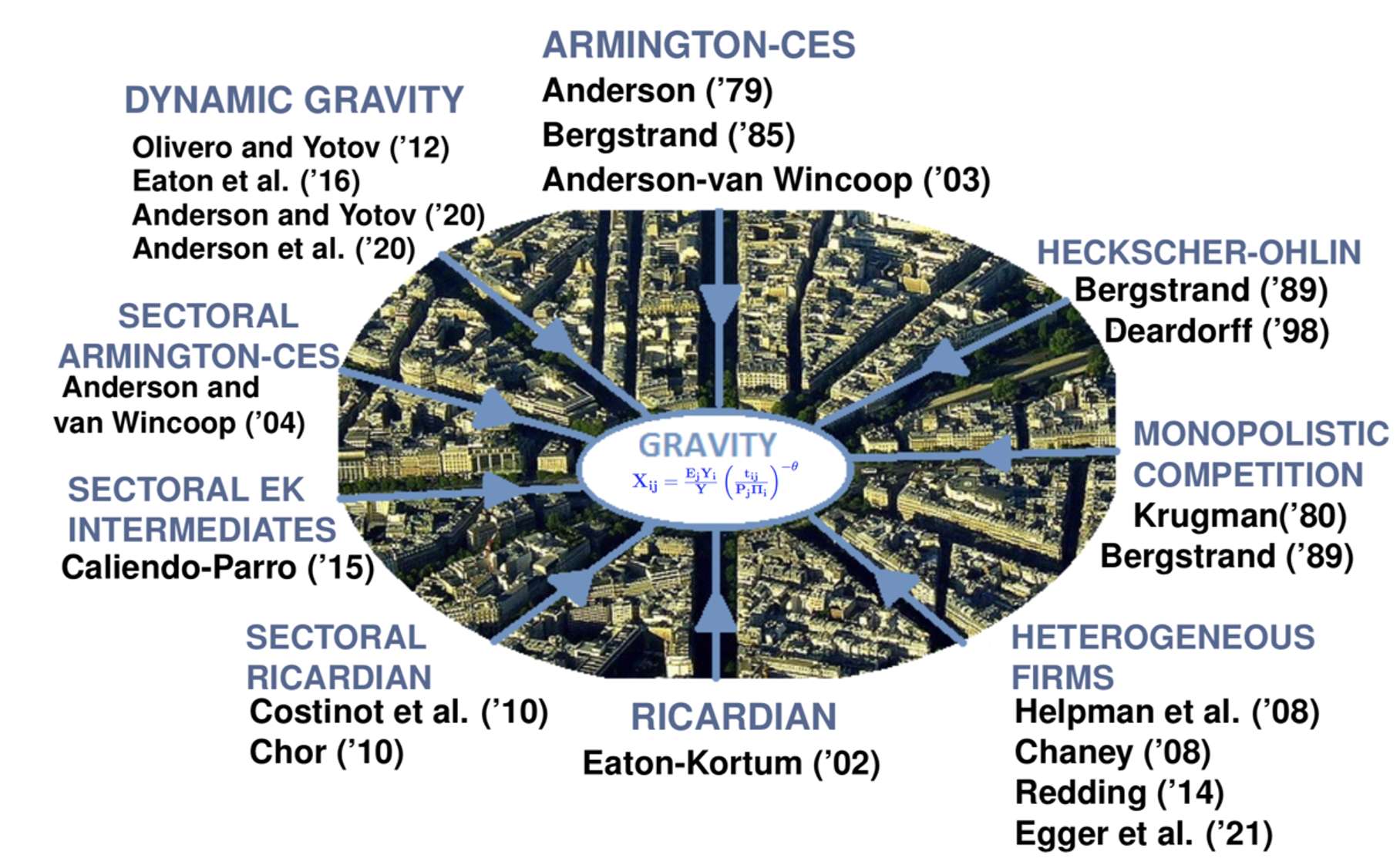
Subject to some inconsistencies (e.g. the proverb says “All roads lead to Rome”, while I use a picture of Paris), Figure 2 visualises the fact that, as seminally demonstrated by Arkolakis et al. (2012), many trade theories deliver exactly the same gravity equation, subject to parameter interpretation.
Figure 2 All roads lead to... gravity
Another important reason why the gravity equation is a popular favourite is that:
Gravity has trememdous predictive power.
Since Tinbergen, whose naive specification obtained R2=0.7, gravity consistently delivers excellent fit and plausible estimates on a number of ‘standard’ covariates, such as distance, free trade agreements (FTAs), and size (Head and Mayer 2014). Borchert et al. (2022) offer disaggregated gravity estimates for 170 sectors in agriculture, mining, manufacturing, and services. Some argue that the remarkable performance of gravity is due to the use of exporter and importer fixed effects, which are standard in gravity regressions. This is not true. Gravity performs quite well without any fixed effects. Remarkably, owing to a special property of the PPML estimator (Fally 2015), one can replace all exporter and importer fixed effects in the gravity regression with just two structural variables, and the fit will remain unchanged. Thus, not only gravity delivers a great fit, but it is a structural estimating model and, therefore, its predictive power is indeed unprecedented.
The next reason for the celebrity status of gravity is that:
Gravity is a very flexible environment.
As such, it has been used to quantify the impact of many determinants of trade in hundreds of academic papers, and it is routinely employed for policy analysis. Most authors rely on gravity to study the effects of ‘traditional’ determinants of trade (e.g. distance and FTAs). Others quantify the effects of more ‘exotic’ determinants of trade (e.g. trust and institutions). A third group of authors use gravity to link trade to other economic outcomes (e.g. growth).
It is safe to conclude that, to study the impact of any determinant on trade or other economic outcomes via trade, one would inevitably resort to some version of gravity.
Traditionally, gravity is used to obtain estimates of the direct effects of policies on trade. However, partial-equilibrium policy analysis alone is inadequate to appropriately quantify big policy changes (e.g. FTAs) because it necessarily misses third party effects that can be important. Gravity, however, is well-suited to conduct GE analysis too, because the estimating gravity equation is part of a GE ‘structural gravity system’.
Gravity is a computable general equilibirium model.
The most famous structural gravity systems are those of Eaton and Kortum (2002) and Anderson and van Wincoop (2003), but Arkolakis et al. (2012) show that many other theories converge to the same gravity system, which delivers two first-order GE effects: ‘trade diversion effects’ and ‘nominal size effects’. Thus, gravity allows researchers and policymakers not only to obtain sound estimates of the direct impact of various policies, but also to easily move from partial equilibrium estimates to first-order GE indexes (i.e. policy effects obtained while holding the supply vector constant) within the same tractable and transparent theoretical framework and with the same data. However, what makes the structural gravity system truly special is that:
Gravity is an estimating-CGE model.
This remarkable property of the structural gravity system is due to two contributions. First is the additive PPML property (Fally 2015), according to which the exporter(-time) and importer(-time) fixed effects from gravity regressions capture exactly and only the corresponding theoretical terms. Thus, the PPML estimator delivers estimates of the GE consumer and producer prices without the need to solve the non-linear gravity system. Second, exploiting the full structure of the gravity system, Anderson et al. (2020) derive a structural estimating equation for income. In combination with the structural estimating gravity equation, the estimating equations for the consumer prices, producer prices, and income make the structural gravity system completely estimating. Anderson et al. (2018) implement the gravity system in Stata to demonstrate how gravity can deliver partial and GE projections with built-in commands (i.e. without custom coding).
The implication is that gravity is a fully self-sufficient estimating-CGE model that can establish causal links and estimate a number of key structural parameters (e.g. trade costs, direct trade policy effects, and trade elasticities) and first-order GE effects within the same tractable model and with the same data that are used for the CGE counterfactuals. Thus, gravity is at least a complement and a benchmark that may provide useful information for calibration and selection of parameter values in more complex CGE structures, which rely on external parameters and assume without testing some important relationships.
The simplicity and tractability of the GE analysis with gravity come with limitations. For example, the factors of production are exogenous (i.e. an endowment setting). Moreover, while the gravity system can be estimated for individual sectors, it does not account for intersectoral linkages. This is why some view gravity as ‘a small-scale’ CGE model. However:
Gravity can be nested within more complex models.
To illustrate the idea, I think of the gravity system as a ‘universal engine’, which can run different vehicles (Figure 3). The fuel for this engine is changes in trade costs. The power and beauty of gravity is that it can structurally translate the changes in the universe of bilateral trade costs into two indexes for each country: an effect on consumer prices and an effect on producer prices. Once gravity ‘collapses’ the bilateral dimension into two country-specific indexes, it is possible to nest the gravity system into many country-specific models from different fields in order to investigate the links between trade and various economic outcomes, such as input-output links (Caliendo and Parro 2015) and sectoral investment dynamics (Eaton et al. 2016).
Figure 3 Nested gravity
The ability to structurally nest gravity in other models has two important implications. First, it means that one can and should still take advantage of all the nice properties of the structural gravity system (e.g. estimate key parameters, establish causal relationships, obtain tractable and transparent first-order GE effects within the same model and with the same data that are used for the counterfactual analysis). Second, assuming the objective is to quantify the effects of trade cost changes, the gravity model must be the heart of the corresponding CGE framework, regardless of how complicated the latter is. Therefore, it is impossible to conduct competent trade policy analysis without taking into account the fundamental, albeit ‘small-scale’, first-order GE relationships that are captured by the structural gravity system. Thus, to me, doing complicated CGE trade policy analysis without (understanding) gravity is like building an impressive skyscraper without a solid foundation.
Gravity continues to be very popular today. As usual, most papers apply gravity to new applications, such as COVID (Baldwin and Dingel 2021), or to improve on existing analysis using better methods or better data, such as re-evaluating the impact of the WTO. Moreover, despite proven success:
Gravity offers many opportunities for new contributions.
For example, on the estimation front, we have better computational abilities, further reassurances for the use of PPML, and new methods to quantify the effects of country-specific determinants of trade. On the theory front, we see new gravity models on the extensive margin of trade and with imperfect competition (Breinlich et al. 2021).
I used late Peter Neary's wisdom to motivate this note, and I will rely on him to end it. In one of our last exchanges Peter commented:
"Gravity is endless fun!"
He was right!
References
Anderson, J E and E van Wincoop (2003), “Gravity with Gravitas: A Solution to the Border Puzzle”, American Economic Review 93(1): 170–192.
Anderson, J E, M Larch and Y V Yotov (2018), “GEPPML: General equilibrium analysis with PPML”, The World Economy 41(10): 2750–2782.
Anderson, J E, M Larch, and Y V Yotov (2020), “Transitional Growth and Trade with Frictions: A Structural Estimation Framework”, Economic Journal 130(630): 1583–1607.
Arkolakis, C, A Costinot, and A Rodriguez-Clare (2012), “New Trade Models, Same Old Gains?,” American Economic Review 102(1): 94–130.
Baldwin, R and J Dingel (2021), “Telemigration and development. How many services jobs will be offshored?”, VoxTalk, 9 November.
Borchert, I, M Larch, S Shikher, and Y V Yotov (2022), “Disaggregated Gravity: Benchmark Estimates and Stylized Facts from a New Database,” Review of International Economics 30: 113-136.
Breinlich, H, H Fadinger, V Nocke. and N Schutz (2020), “Gravity with Granularity”, VoxEU.org, 21 November.
Caliendo, L and F Parro (2015), “Estimates of the Trade and Welfare Effects of NAFTA,” Review of Economic Studies 82(1): 1–44.
Eaton, J and S Kortum (2002), “Technology, Geography and Trade”, Econometrica 70(5): 1741–1779.
Eaton, J, S Kortum, B Neiman and J Romalis (2016), “Trade and the Global Re- cession,” American Economic Review 106(11): 3401–38.
Fally, T (2015), “Structural Gravity and Fixed Effects,” Journal of International Economics 97(1): 76–85.
Head, K and T Mayer (2014), “Gravity Equations: Workhorse, Toolkit, and Cookbook”, Chapter 3 in G Gopinath, E Helpman, and K S Rogoff (eds), Handbook of International Economics, Vol. 4, Elsevier.
Tinbergen, J (1962), Shaping the World Economy: Suggestions for an International Economic Policy, Twentieth Century Fund.
Yotov, Y V (2022) “Gravity at Sixty: The Bijou of Trade”, Drexel School of Economics Working Paper 2022-01.