Social and professional networks are pervasive in our everyday lives and, directly or indirectly, they influence our choices and their behaviour. For example, the decision to engage in crime is affected by the social environment (Jackson 2008 and Bramoullé et al. 2016 provide overviews). These agents do not have a perfect knowledge of their environment, and that is an important aspect of their decision. For example, when someone decides to commit a crime, she does not know with certainty the probability of being caught and, if caught, how severe the punishment would be. As a result, would-be criminals need to form expectations about these aspects. In a social network context in which agents are affected by their peers, they also need to form expectations about the actions of their peers, the actions of their peers' peers, and so on (in other words, ‘higher order beliefs’).
We study these questions by developing a Bayesian network game in which players, embedded in a network of social interactions, bear a cost from deviating from the social norm of their peers (Rapanos, Sommer, and Zenou 2019). They face uncertainty about the private benefits and the private and social costs of their actions.
These parameters are potentially heterogeneous across players and consist of two components: a global component is common to all players, and represents the universal or invariant payoff or cost resulting from an action; an idiosyncratic component captures the part of benefit or cost of the action that depends on the individual characteristics of each individual.
To model uncertainty, each player is assumed to observe some (potentially noisy) signal about the value of these payoff parameters, based on which she optimally chooses an action. Agents are directly affected only by the choices of their immediate neighbours in the network, but they also need to infer the actions of players located more than one link away, since these 'higher-order neighbours' may affect their immediate neighbours, who in turn affect them. Because of linear best responses, Nash equilibrium outcomes will depend on higher-order average expectations.
A framework
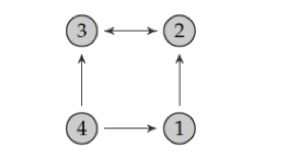
To illustrate this model, consider the following network of four criminals. A direct link (outdegree) from offender i to offender j signifies that offender j belongs to the reference group of offender i and can be interpreted as offender i paying attention to the behaviour of offender j – or, alternatively, offender j being a role model to offender i. In this network, we see that offender 1’s reference group (or social norm) consists of offender 2, offender 2’s reference group of offender 3, offender 3’s reference group of offender 2, and offender 4’s reference group of offenders 1 and 3.
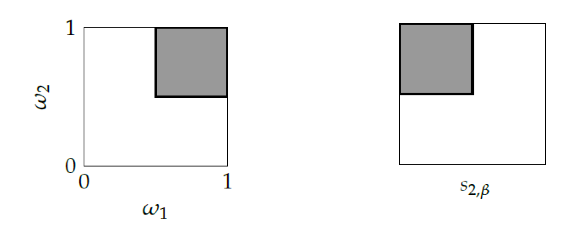
A key element that affects an individual’s decision about whether to commit a crime, and to what extent, is the perception of the probability of being apprehended and convicted. The fraction of police officers on duty in a precinct, denoted by ω1 ∈ [0,1], and a measure of the strictness of the judge or jury, denoted by ω2 ∈ [0,1], constitute the state of nature ω, that is, ω = (ω1,ω2), ∈ [0,1]2.
To illustrate this, consider offender 2 and assume that offender 2’s private cost of committing crime is given by the left-hand panel of Figure 1.
Figure 1 The private cost and private signal of the cost of committing a crime
Source: Rapranos et al. (2019).
Assume two states of nature: the high state is when the cost of committing crime is high, and the low state is the opposite. The area shaded in dark grey corresponds to the high state – that is, if a lot of police officers are on duty in this precinct (high ω1) and there is a tough sentencing judge (high ω2). The white area corresponds to the low state.
Assume that the private signal of offender 2 is given by the right panel of this figure. This signal is partially informative about the state of nature. There is no uncertainty about the value of the cost that gives rise to a high signal value (the area shaded in dark grey) since offender 2 knows with certainty that the state is low. As a result, starting with the prior that the probability of having a low cost (high cost) of committing crime is 3/4 (1/4), offender 2 updates her beliefs as follows: if she receives a low signal, the probability of low cost is 2/3 and that of high cost is 1/3. If she receives a high signal, then she knows with certainty that the state is low.
Equilibrium
We can calculate the Bayesian-Nash equilibrium of this game with four offenders who choose the crime effort to maximise their utility, for which they seek to minimise the distance between their effort and that of their social norm. Table 1 shows the equilibrium values.
Table 1 Bayesian-Nash equilibrium of the crime network game
| Offender |
Effort |
Payoff |
Social norm |
|---|
| 1 |
1.49 |
0.77 |
1.40 |
| 2 |
1.40 |
0.62 |
1.52 |
| 3 |
1.52 |
0.79 |
1.40 |
| 4 |
1.42 |
0.76 |
1.51 |
Source: Rapranos et al. (2019).
In equilibrium, offender 3 exerts the highest effort, has the highest payoff, but faces the lowest social norm so that her effort is above her social norm. In contrast, offender 2 makes the lowest effort, obtains the lowest payoff, and faces the highest social norm so that her effort is below her social norm.
This shows that imperfect information about the presence of police in one’s neighbourhood and the severity of the judge if someone is arrested strongly affect offenders’ behaviour. This should be taken into account if one wants to address policies aiming at reducing crime. Policy interventions may aim to change the payoff parameters, the network structure, or the availability and quality of information.
Changing the network
One set of policies would focus on cutting the communication and influence channels between offenders. An interesting, counter-intuitive finding is that severing directed links, even between relatively active offenders, does not necessarily lead to a decrease in the aggregate level of crime. This implies that, under relatively weak assumptions, a dense criminal network may be associated with a lower overall crime rate than a sparser network.
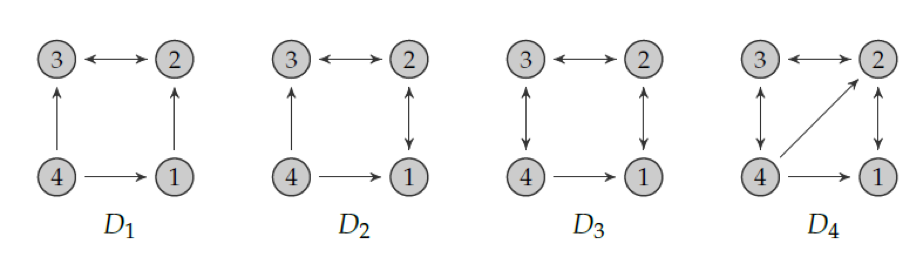
To discuss the effects of changes in the topology of the network that connects offenders, we consider a network formation game over four periods of time. In the first period, the network is as above (we call it Network D1). In every period τ=2,3,4, offender τ expands her reference group by forming a single directed link to another offender such that the new directed link benefits her most (in terms of ex ante expected equilibrium payoff). The resulting sequence of networks D1, D21, D3, D4 is displayed in Figure 2, and the outcomes in Figure 3.
Figure 2 Expanding the reference groups of offenders in the crime network game
Source: Rapranos et al. (2019).
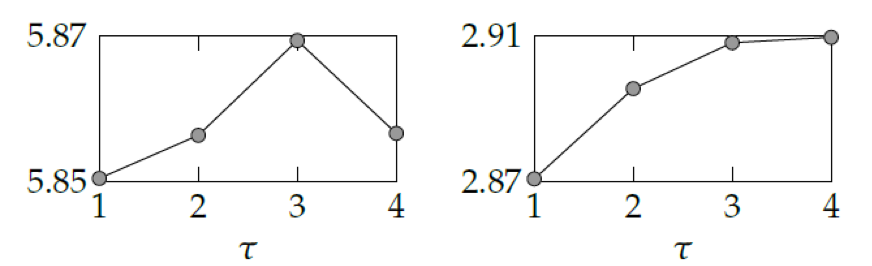
Figure 3 Outcomes of crime game network game: total crime (left-hand panel) and welfare (right-hand panel)
Source: Rapranos et al. (2019).
We see that the effect of having a denser network (from D1 to D2 to D3 to D4) has a non-monotonic impact on total crime (aggregate effort) and an increasing and concave effect on total welfare. This is because, when the number of links increases in the network, the social norm of each offender changes and therefore they change their criminal behaviour accordingly as they want to reduce the distance between their effort and their social norm.
So policy may seek to isolate a convicted offender from the reference group by enforcing restrictions on association, location, or residence. The policy seeks to decrease network density, but this result suggests that, even if successful in doing this, it would not necessarily reduce aggregate criminal activity. Note, however, that this non-monotonicity is rooted in the design and the structure of the crime network game.
Implications of the gap between actual and perceived risks
One of the most important questions for perceptual deterrence research is the degree of correspondence between actual and perceived risks and the role of social norms. In particular, if perceptions do not closely mirror reality, which means that the signal is uninformative about the cost of committing crime, then changes in policy will go unnoticed by potential offenders. In that case, the outcomes of policy research will tend to be of limited value in studying deterrence.
For example, Blanes i Vidal and Mastrobuoni (2018) show that if offenders do not know the presence of police in their area, so that there is a large gap between the actual and perceived risks of being caught, then increasing the number of police in an area has no effect on crime deterrence. We also model the influence of direct friends or co-offenders on own-crime activity and, therefore, how the gap between the actual and perceived risks of committing crime of one’s friends affects own criminal activities.
We believe that these are important issues because in order to address adequate policies aiming at reducing crime, we need to understand how offenders would react and change their beliefs when there is an increase in police, or an increase in punishment. Using Norwegian data, Bhuller et al. (2018) estimate the effect of the punishment of criminals on their co-offenders and their brothers. Using the quasi-random assignment of criminal cases to judges, they show that when a defendant is sent to prison, there are reductions of 51 and 32 percentage points, respectively, in the probability his criminal network members and younger brothers will be charged with a crime over the ensuing four years.
Our model can provide an explanation of these empirical results. When a criminal is facing a 'tough' judge, she updates her beliefs about the severity of crime punishment and transmits this information to her co-offenders and younger brothers. In turn, they update their own beliefs and, as a result, reduce their criminal activities.
References
Bhuller, M, G B Dahl, K V Løken, and M Mogstad (2018), "Incarceration Spillovers in Criminal and Family Networks", unpublished manuscript, University of Chicago.
Bramoullé, Y, B W Rogers, and A Galeotti (2016), The Oxford Handbook of the Economics of Networks, Oxford University Press.
Blanes i Vidal, J, and G Mastrobuoni (2018), "Police Patrols and Crime", IZA discussion paper 11393.
Jackson, M O (2008), Social and Economic Networks, Princeton University Press.
Rapanos, T, M Sommer, and Y Zenou (2019), "Imperfect Information, Social Norms, and Beliefs in Networks", CEPR Discussion Paper 14087.