Should Barack Obama worry about the Bradley effect? The much-discussed effect refers to observed discrepancies between voter opinion polls and election outcomes, in which African-American candidates receive a smaller vote share than would be predicted using opinion polls. In this column, I study US congressional and gubernatorial contests from 1998 to 2006 – black candidates on average receive a 2-3% lower share of the two-party vote than non-black candidates with similar numbers in the polls. If an effect of a similar size would appear in the current presidential race, then it would lower Obama’s probability of winning from 85% to 53%. However, black Republican candidates drive the result, so it may not apply to Obama’s campaign.
Data
My sample includes 431 elections for the offices of House, Senate and Governor 1998-2006 for which I have election and opinion poll data and information on whether the candidate was black. The data on elections was provided by Jim Snyder at MIT, the data on candidate race is from the Joint Center for Political and Economic Studies, and the polling data was gathered from various sources. This data is similar to that of Daniel Hopkins (2008), who uses data from 133 gubernatorial and Senate elections from 1989-2006.
There are 26 black candidates in the sample, 17 Democrats and 9 Republicans (4 in gubernatorial races, and 11 each for the offices of House and Senate). I will only analyse races where a black candidate ran against a candidate who was not black. This eliminates two races, one of which is Barack Obama’s race for Senator of Illinois against Alan Keyes in 2004. I am left with 22 races. The relevant sample of 22 elections is quite small, so all results should be taken with a grain of salt (still, the sample is larger than existing studies).
The 2-3% Bradley effect
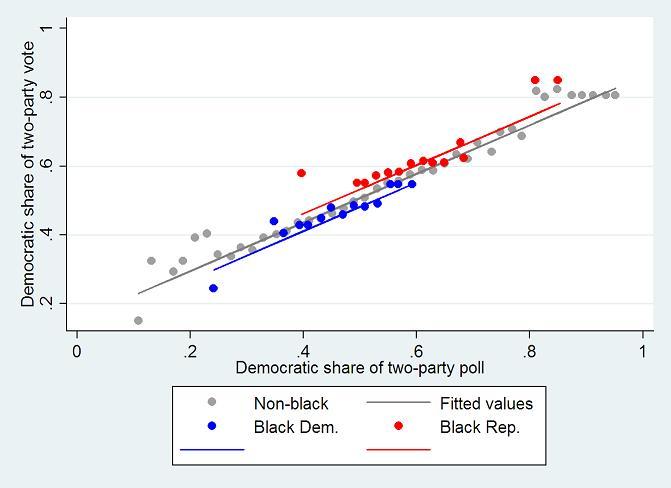
Figure 1 shows the relationship between polling and vote outcomes for races for House, Senate and Governor 1998-2006. I only include polls performed from August to the date of the election. Each dot shows the poll and vote average within each two-percent opinion poll interval, 0-2, 2-4, etc. The grey dots are non-black candidates, the blue dots are black Democratic candidates, and the red dots are black Republican candidates. The grey line shows the fitted values of a regression of Democratic vote share on Democratic poll share, for non-black candidates. As you can see, black candidates on average do worse than other candidates polling at the similar numbers in the polls: Democratic black candidates more often lie below the regression line (expected vote, conditional on poll) and Republican black candidates more often lie above.
Figure 1. Democratic vote and poll shares
This is confirmed in a regression analysis, see Table 1. The first column shows the results from a regression of the Democratic two-party vote share on the Democratic two-party poll share in the full sample. The coefficient on poll is less than one, indicating that the lagging candidate typically does better in the election than in the polls. The variable Black Democratic candidate second column adds a variable that equals one if a black Democratic candidate is running against a non-black Republican, –1 if a black Republican candidate is running against a non-black Democrat, and 0 otherwise. The estimate of –0.025 implies that when there is a black Democratic (Republican) candidate, then the expected Democratic (Republican) vote share is 2% lower. In other words, a black candidate forecast to win against a non-black 52.5% to 47.5% in fact, has no lead when race is taken into account.
Table 1. Democratic share of the two-party vote
| |
I |
II |
III |
IV |
V |
VI |
| Democratic share of two-party polls |
0.707 |
0.68 |
0.718 |
0.685 |
0.665 |
0.696 |
| |
(0.029)*** |
(0.038)*** |
(0.031)*** |
(0.041)*** |
(0.137)*** |
(0.149)*** |
| Black Democratic candidate |
-0.025 |
-0.024 |
-0.028 |
-0.026 |
-0.028 |
-0.029 |
| |
(0.006)*** |
(0.006)*** |
(0.006)*** |
(0.006)*** |
(0.010)*** |
(0.011)** |
| Incumbent |
|
0.009 |
|
0.011 |
|
|
| |
|
(0.004)** |
|
(0.005)** |
|
|
| Partisan poll |
|
-0.014 |
|
-0.014 |
|
|
| |
|
(0.003)*** |
|
(0.004)*** |
|
|
| Constant |
0.153 |
0.167 |
0.149 |
0.166 |
0.185 |
0.165 |
| |
(0.015)*** |
(0.020)*** |
(0.017)*** |
(0.022)*** |
(0.072)** |
(0.078)* |
| Observations |
2481 |
2400 |
2017 |
1961 |
200 |
179 |
| R-squared |
0.735 |
0.754 |
0.766 |
0.781 |
0.848 |
0.891 |
Notes: Standard errors, clustered by election, in parentheses. * significant at 10%; ** significant at 5%; *** significant at 1%.
The next column adds the variable Incumbent, taking the value 1 if the incumbent is Democrat, -1 if the incumbent is Republican, and 0 if there is no incumbent running. Even taking the polls into account, the incumbent has a 1% advantage. This specification also adds the variable Partisan poll, taking the value 1 if the pollster’s name contains (D) or Democratic, -1 if the pollster’s name contains (R) or Republican, and zero otherwise. The estimate tells us that we should discount partisan pollsters’ numbers by 1.4%.
The next two columns repeat the previous two specifications for Senator and Governor races only. For House races, I have mainly been able to obtain internal/partisan campaign polls that had been "leaked" to the media, which in many cases I would not consider reliable.1 Also, I only have opinion poll data for a few House races and selection bias may be an issue, as I will discuss further below. The final two columns include only contests for which there was one black and one non-black candidate, with and without House races.
Table 2 contains the same specifications as Table 1, but only uses the last poll available before the election. The results are similar, although estimates are less precise as the number of observations is radically reduced.
Table 2. Democratic share of the two-party vote, last poll before election
| |
I |
II |
III |
IV |
V |
VI |
| Democratic share of two-party poll |
0.673 |
0.639 |
0.755 |
0.693 |
0.766 |
0.837 |
| |
(0.022)*** |
(0.026)*** |
(0.028)*** |
(0.034)*** |
(0.106)*** |
(0.066)*** |
| Black Democratic candidate |
-0.021 |
-0.02 |
-0.031 |
-0.029 |
-0.023 |
-0.022 |
| |
(0.010)** |
(0.010)* |
(0.014)** |
(0.013)** |
-0.015 |
(0.011)* |
| Incumbent |
|
0.011 |
|
0.018 |
|
|
| |
|
(0.004)*** |
|
(0.005)*** |
|
|
| Partisan poll |
|
-0.016 |
|
-0.024 |
|
|
| |
|
(0.005)*** |
|
(0.013)* |
|
|
| Constant |
0.164 |
0.182 |
0.125 |
0.155 |
0.146 |
0.091 |
| |
(0.011)*** |
(0.013)*** |
(0.014)*** |
(0.017)*** |
(0.056)** |
(0.035)** |
| Observations |
431 |
421 |
213 |
211 |
22 |
13 |
| R-squared |
0.707 |
0.733 |
0.794 |
0.811 |
0.859 |
0.982 |
Notes: Standard errors in parentheses. * significant at 10%; ** significant at 5%; *** significant at 1%.
Why does these results suggest a Bradley effect?
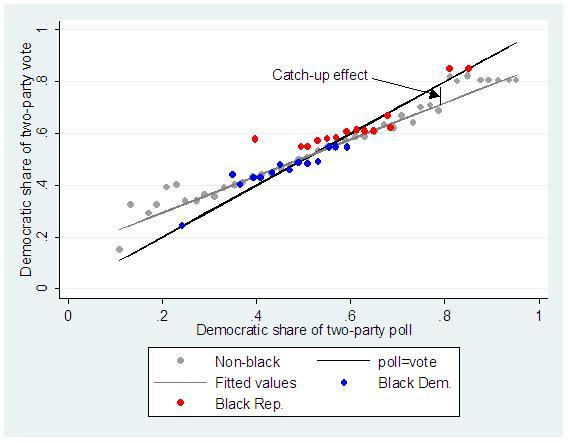
The most-discussed recent study of the Bradley effect is Hopkins (2008). He finds no Bradley effect. The reason, I think, is that he compares election outcomes to polls and does not correctly account for the fact that black candidates more often are lagging. This is shown graphically in Figure 2, which as Hopkins, only include races for Senate and Governor. Black candidates are behind in the polls: there are few black Democratic candidates in races where Democrats have more than half of the polls share, and few black Republican candidates in races where the Republicans have more than half of the polls share. The lagging black candidates’ votes are close to their poll shares (the black line), but this is worse than the average lagging non-black candidate that typically gets a result closer to 50-50 than the polls indicated.
Figure 2. Votes and polls in contests for Senate and Governor with black candidates
The catch-up effect is measured by the difference between the poll share (black line) and the expected vote share of non-white candidates (grey line). At 20% support in the polls, the lagging candidate is expected to catch-up around 3.5% in vote shares compared to polls shares, at 40% in the polls the catch-up effect is around 1%. This means that a lagging black candidate at 30% poll shares is expected to gain 2% from the catch-up effect, and to lose 2% from the Bradley effect. So this observation should be on the 45-degree line.
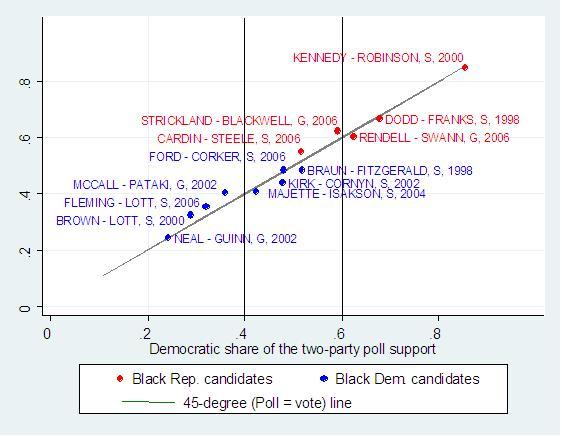
If we want to measure the Bradley effect from the difference between polls and vote shares, we can do this in close races where the catch-up is small. In Hopkins’ sample, like mine, the average difference between the black candidates’ opinion poll shares and their vote shares is zero. However, in the sub-sample of close elections, where the black candidate has 45-55% in the polls, the mean difference between elections and polls is –3.5%. The gap is –2.3% in races where the black candidate polls between 40-60%. Absent the catch-up effect, the black candidates do worse than the polls. Note that 40-60% races seem the relevant comparison with Obama, since he is not lagging. For concreteness, Figure 3 shows the details of the races included and the 45-degree line. Note the small number of close elections: six races containing three races in 2006, and one race each in 1998, 2002 and 2004.
Figure 3. Votes and polls in contests for Senate and Governor with black candidates
How much does this matter for the presidential race?
There are all sorts of issues in applying these estimates from congressional and gubernatorial contests to presidential elections. They are inherently different, and the states and districts with black candidates are not representative of the states important for the outcome of the presidential election. It may also be that Obama appears as “less black” than the average candidate in my sample, that there are larger shares of young, black and Hispanic voters than in previous contests, etc. Still, it is useful to gauge how much the presidential race would change with a similarly sized Bradley effect.
I do this using the forecasting model of presidential elections from my recent paper in the American Economic Review (Strömberg 2008). It uses a vote-forecast equation based on opinion polls similar to that estimated above. It is straightforward to add the estimated black candidate effect (estimated from the last poll) to that model.
Without the Bradley effect, Obama has an 84% chance of winning, receiving 52% of the two-party vote share. (Obama is expected to receive 52% even though he is polling at 53% of the two-party vote share, because of the catch-up effect.) However, the race is a coin flip if the presidential race will exhibit a Bradley effect of the same size as the average for the 22 House, Senate and Governor races 1998-2006 for which I have data. Obama’s win probability drops to 53%, with an expected vote share of 49.9.
A caveat. The Bradley effect seems more severe for Republican than Democratic black candidates. This can be seen in Figure 1, as the Republicans lie further from the regression line than the Democrats. Although we rely on very small samples when estimating the effects in sub-groups, only the effect of the nine Republican black candidates is significant when one allows for separate effects by party.
Some final issues
The probability of winning may be related the Bradley effect in a non-linear way. To investigate this, I simulated the probability of winning, drawing 100 draws from the estimated distribution of the Bradley coefficient: a normal distribution with the estimated mean of 2.3% and variance of 1.1%. This gave me an almost identical result to using the mean, Obama’s win probability is 53% and his expected vote share is 49.8%. My intuition is that this is because the mean effect of 2.3% brings the probability of winning close to 50-50 and the Bradley effect is roughly linear around that point.
There may be a selection bias in the set of races where polls are available, e.g., races where it is "surprising" that a black is doing quite well against a non-black (perhaps too well). However, for the set of races for Governor and Senator, this unlikely to be an issue, since I have opinion polls for all races with black candidates for even years 1998-2006. There is a significant Bradley effect in these races.
Of course, the possibilities of small sample bias are huge. The bottom line – based on recent elections for House, Senator and Governor, there is weak evidence to support the Bradley hypothesis. In contrast to Hopkins (2008), I conclude that there is no evidence to reject it.
References
Stromberg, David (2008). "How the Electoral College Influences Campaigns and Policy: The Probability of Being Florida. " American Economic Review, 98(3): 769–807.
1 I thank Nate Silver for pointing this out to me.