A vital challenge confronting economists is how to forecast. The task is yet more exacting but ever more pertinent during a recession because livelihoods seem to depend on forecasts – will unemployment fall soon enough to stave off foreclosures?
Perhaps unsurprising then is a recent clash in the blogosphere over forecasting US GDP in the coming quarters. Greg Mankiw contested the US government’s forecasts of GDP growth, questioning the trend stationarity assumption upon which the forecasts were made. Paul Krugman wrote an outraged response, accusing Mankiw of “evil wonkishness”. Brad DeLong weighed in too, pointing out that a univariate analysis was “useless”; unemployment must be included in the analysis.
The exchange emphasises not just that economic variables are important in forecasts, but that econometric issues matter. If GDP is trend stationary, the implications are very different for forecasting than if GDP is a random walk with drift – one will correct to some equilibrium, the other won’t. Economic nuances matter too – what other variables make up this equilibrium relationship? Historically, there has been such a steady state, but whether that is the same one to which we will soon correct is unclear, and bad forecasts may result.
Finally, much has been made of prediction markets as effective forecasting models (Wolfers and Zitzewitz 2004). Market participants in prediction markets buy and sell contracts whose payoff is contingent on a particular event happening, such as a recession in the US by the end of 2008. Evidence suggests that such markets are well calibrated; if a contract is at 90%, then 9 times out of 10 that contract will pay out (Smith, Paton and Vaughan-Williams 2006; Croxson and Reade 2008). Perhaps the way forward is to forecast using prediction markets?
Judging forecasts
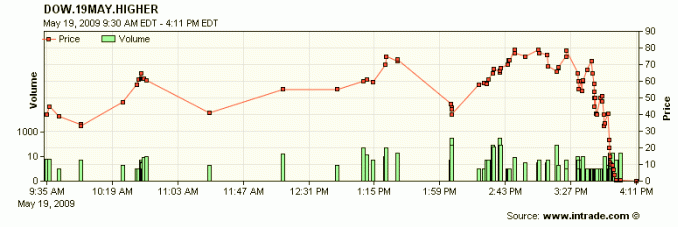
With econometric models of forecasting, we tend to only consider one realisation of reality and judge model and strategy. This is somewhat akin to judging InTrade, one of the most popular prediction markets, based on one market, for example the “Dow to close higher than previous close” market, plotted above for June 9 2009. Even at 3:45pm the market was priced at 88, implying a 88% chance of the Dow ending higher. As can be inferred, the Dow ended lower. But based on the 3:24pm price for 1000 days, this may have been one of the 120 contracts to efficiently fail to pay out. The technique followed for forecasting matters, and we should not judge it based on one realisation.
Figure 1. An InTrade realisation
Prediction markets, particularly on frequent similar events such as soccer matches, provide an excellent natural “simulation” study to determine forecast accuracy. By considering thousands of sports matches, we can ascertain the accuracy of prediction markets. With the economy, and with econometric methods for forecasting, we generally do not have such ability. Monte Carlo simulation affords us something akin to this. We generate thousands of artificial datasets, run our models and assess the outcomes. If a technique performs well in simulation, then we might consider using it to forecast the next period, just as we might consider using the InTrade price for an economic recovery in 2009Q1 as an accurate forecast given its track record.
Of course, trusting prediction markets to forecast well in the future relies on the assumption that the event they are predicting is stationary; that soccer matches do not suddenly change in their nature overnight – the goals aren’t widened or the rules drastically altered. In that non-stationary situation, it would be impossible to know whether InTrade would continue to forecast well.
Prediction markets can be viewed as a form of forecast pooling or model averaging, a common forecast technique (Bates and Granger 1969, Hoeting et al 1999 and Stock and Watson 2004). That is, forecasts from different models are combined to produce a single forecast. In prediction markets, each market participant makes a forecast based on his or her own forecasting model, and the market price is some function of each of these individual forecasts.
Averaging forecasts
Averaging forecasts is motivated by the perceived difficulty of choosing a single model. It is often not clear in advance which model will forecast best, thus we take the insurance of averaging over a number of models. We forecast worse than the best model (the premium), but we forecast better than the worst model (the pay out) by smoothing forecast errors.
However, is this a sensible strategy? Do we do better by averaging? The alternative to averaging forecasts is to select one particular forecast, but framed in the context of 2K possible models for K variables in a dataset, choosing the “right” model seems an impossible task when K is at all large.
But judging success of selecting a model by whether one selects the “true” model is not a useful metric. There will be many models quite similar to the “true” model that will also perform well, and selecting any one of these models is a more realistic target than just choosing the “true” model. Furthermore, that metric would rule out using standard statistical tests on the “true” model: one t-test in a four-variable true model with true t-ratios of 4 for each variable would reject 10% of the time (Hendry and Krolzig 2005).
General-to-specific modelling vs. forecast averaging
Hendry (1995) emphasised a general-to-specific strategy of starting with the most general empirical model possible. This general model would incorporate variables from all economic theory and previous econometric work. It should also be well specified, satisfying the assumptions placed on the statistical model. From there, a search would begin for the simplest model that still satisfied the statistical assumptions.
Hoover and Perez (1999) and Hendry and Krolzig (1999, 2002, 2005) automated this procedure into a program, allowing multiple path searches. Monte Carlo simulation of such search algorithms allows something akin to the calibration testing described above, giving a way to assess how well the algorithm performs.
The metric of success to judge between strategies might be forecast success – how often will a forecast turn out accurately? Furthermore, other strategies for forecasting such as averaging can be compared in this context. This is precisely what we have done in recent research, presented at the Royal Economic Society Conference in April.
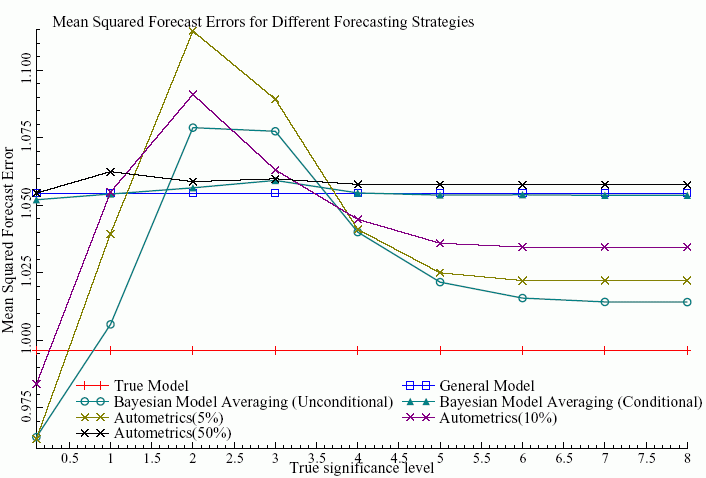
We find that the differences between a forecast from an averaged set of models performs about as well, and sometimes worse, than a forecast from a model selected by the available general-to-specific model selection package, Autometrics.1 The figure below plots the mean squared forecast error for a number of forecasting strategies for different levels of significance of variables.
No clear winner emerges. The simulation uses datasets in which the variables are essentially uncorrelated with each other, and free from misspecification. Five of the ten variables in the general model are significant, and their significance rises along the horizontal axis.
Forecasting methods that involve significance-based selection between the 10 variables suffer when the true significance level is around 2. This “hump” is caused by type-II errors – relevant variables are incorrectly omitted causing larger forecasts. This is true for model selection with Autometrics with a 5% or 10% significance level, and is also true for Bayesian Model Averaging (BMA), when model weights are not scaled to sum to unity for a particular regressor (unconditional). Both penalise bad models or insignificant variables.
On the other hand, these methods perform better when variables are potentially very significant, or not at all significant. Methods that do not omit these borderline variables, do not exhibit the hump. Conditional BMA, where weights are scaled to sum to unity for each variable, and Autometrics with a 50% significance level (essentially accepting all variables) do not have a hump but instead produce higher forecast errors throughout.
Our simulations are on simple, small datasets, yet undoubtedly have implications for wider work. The performance of averaging depends on selection; How do you select the set of models you average over? Averaging does not escape the difficulties of selection – bad forecasts must be omitted from those averaged over.
Non-stationarity has been mentioned – our simulations in that context appear to reverse many of the orderings of forecasting methods found in the stationary case above. Clements and Hendry (2004) provide some reasons why this might be the case.
Fortunately, the econometric theory of model selection has advanced, as have computer packages implementing it automatically. Doornik (2009) compares Autometrics to other well-used selection packages, such as stepwise regression, and find Autometrics performs much more effectively.
Conclusion
One must take forecasting technique seriously, and issues surrounding model selection cannot be ignored. Good forecasts rely on good models, regardless of how the final forecast is composed. A prediction market populated by toddlers will not forecast the next UK election winner simply because it is a prediction market.
References
Bates, J. M. C. W. J. Granger (1969) The Combination of Forecasts, OR, Vol. 20, No. 4 (Dec., 1969), pp. 451-468
Clements, Michael P. and Hendry, David F., Pooling of Forecasts. Econometrics Journal, Vol. 7, No. 1, pp. 1-31, June 2004.
Croxson and Reade (2008). “Information and Efficiency: Goal Arrival in Soccer Betting.”
Doornik, J.A. (2009), ‘Autometrics’, in ‘The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry’, Castle, J.L and Shephard, N. (eds.), OUP, Oxford.
Hendry, David F. (1995). Dynamic econometrics. Oxford University Press.
Hendry, David F. and Hans-Martin Krolzig (1999). “Improving on 'Data mining reconsidered' by K.D. Hoover and S.J. Perez.” Econometrics Journal 2(2): 202-219.
Hendry, David F. and Hans-Martin Krolzig (2002). “New Developments in Automatic General-to-specific Modelling.”
Hendry, David F. and Hans-Martin Krolzig (2005). “The Properties of Automatic GETS Modelling” Economic Journal, Vol. 115, No. 502, pp. C32-C61, March 2005
Hoeting, Jennifer A. David Madigan, Adrian E. Raftery, Chris T. Volinsky (1999) Bayesian Model Averaging: A Tutorial , Statistical Science, Vol. 14, No. 4 (Nov., 1999), pp. 382-401
Hoover, David and Stephen Perez (1999). “Data mining reconsidered: Encompassing and the general-to-specific approach to specification search.” Econometrics Journal 2, pp. 167–191.
Smith, Michael A., Paton, David and Vaughan Williams, Leighton, Market Efficiency in Person-to-Person Betting. Economica, Vol. 73, No. 292, pp. 673-689, November 2006
Stock JH, Watson MW. 2004. Combination forecasts of output growth in a seven country dataset. Journal of Forecasting 23: 204–430.
Wolfers, Justin and Eric Zitzewitz (2004) Prediction Markets, The Journal of Economic Perspectives, Vol. 18, No. 2 (Spring, 2004), pp. 107-126
1 Autometrics (Doornik, 2009) is available with OxMetrics (Hendry and Doornik, 2009), available from www.doornik.com or www.timberlake.co.uk.