Decisions about consumption, work, leisure, pricing, investment, and other private and public policy decisions rely on forecasts of the future. The ‘permanent-transitory confusion’ refers to the fact that, even when they know all past and current information, individuals are uncertain about the persistence of the current state. This all-pervasive informational limitation makes it optimal, in general, to use all past information when forecasting the future even under rational expectations.
The importance of the permanent-transitory confusion for current decisions cannot be overemphasised. Friedman’s (1957) permanent income hypothesis requires separating the current permanent component of income from past and current transitory movements in income. Lucas and Rapping (1969) highlight the importance of identifying whether a period of layoffs is permanent or not for career and employment decisions. More generally, separating the persistent components of demand and productivity from their past transient movements is a basic determinant of firms’ pricing and production decisions, as well as of monetary policy decisions of central banks.
The objective of this column, drawing on Cukierman (2009), is to remind the profession of this basic fact and to point out some of its implications. I do so by showing at both the theoretical and the empirical levels that forecasts of the future are generally adaptive in the sense that they depend on available past information even when information is utilised efficiently. This is done along the following dimensions: first, by showing that the permanent-transitory confusion injects the past even into purely forward-looking New-Keynesian frameworks such as that of Clarida et al. (1999); second, by showing empirically that inflationary expectations in the US Survey of Professional Forecasters rely on past inflation.
In the presence of the persistent-transitory confusion, the past is a guide for the future even in purely forward-looking rational expectations models
The claim in the title of this section is illustrated within the framework of Clarida et al. (1999). This early New-Keynesian model is purely forward-looking, which implies that inflation persistence is due solely to gradual adjustments of individual prices through the Calvo coefficient.
However, empirical studies of the Phillips curve reveal that the inflation process is more persistent than can be justified by the Calvo coefficient (Fuhrer and Moore 1995, Fuhrer 1997). Roberts (2001) finds that the New-Keynesian purely forward-looking Phillips curve does not fit the US data well. In particular, this equation requires additional lags of inflation not implied by the model under rational expectations. Gali and Gertler (2000) and Steinsson (2003) propose hybrid modifications of the purely forward-looking Phillips curve that is consistent with higher inflation persistence. In those specifications, a certain fraction of backward-looking producers is assumed to set their prices as a function of past inflation. This assumption implies that the inflationary expectations of the backward-looking firms are not rational.
In the third section of Cukierman (2019), I show that, in the presence of the persistent-transitory confusion and under rational expectations, inflation, the output gap, expected inflation, and interest rate policy all depend on past observations of relevant shocks even in purely forward-looking models. The reason is that under persistent-transitory confusion, the persistent Markov component is mixed with a white noise process. Note that the persistent-transitory confusion differs from Muth’s (1960) pioneering formulation of the permanent-transitory confusion since, in the latter case, the stationary Markov component is replaced by a random walk. However, none of these processes is ever observed separately, implying that the optimal predictor of the Markov component depends on all past history. One implication of this result is that it is not necessary to introduce ad hoc assumptions about the backward-looking behaviour of price setters in order to justify the empirical appearance of past variables in hybrid New-Keynesian models.
This is demonstrated within a modified, compact form of the Clarida et al. (1999) model.1 The main novelty of the modified variant is that it acknowledges explicitly the existence of a persistent-transitory confusion concerning the mark-up/cost push shock in the New-Keynesian Phillips relation. This is done by replacing the first-order Markov process postulated by Clarida et al. (1999) with a process that feature the persistent-transitory confusion.
The main result of this exercise is that inflation, the output gap, expected inflation, and interest rate policy all depend on past observations of the cost shock in spite of the fact that the model is purely forward-looking. Since the cost shock is subject to the persistent-transitory confusion, the optimal predictor of the persistent component depends on the entire past history of the shock. The dependence of the endogenous variables on this same history is a consequence of the fact that both expected inflation and the expected output gap affect all endogenous variables in the model. A central implication of this result is that it is not necessary to introduce ad hoc assumptions about the backward-looking behaviour of price setters in order to justify the empirical appearance of past variables in hybrid New-Keynesian models.
An empirical application of the persistent- transitory confusion to professional forecasts of inflation
The previous sections imply that in stochastic processes that feature the persistent-transitory confusion or the permanent-transitory confusion, rational expectations rely on past information. In this section I use data on professional inflation forecasts in order to examine whether those directly measured expectations rely on data from the past or not. The data come from the US Survey of Professional Forecasters that is collected and maintained by the Federal Reserve Bank of Philadelphia. I use quarterly data on one year ahead average forecasts between 1981 and 2017.
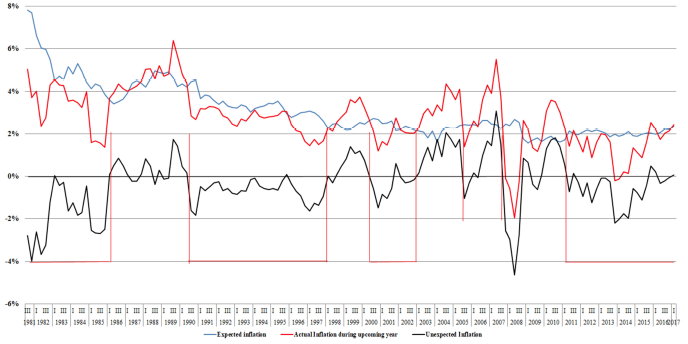
Figure 1 shows actual (in red) and expected (in blue) inflation as well as unexpected inflation (in black). The main regularity that emerges from the figure is that, more often than not, during periods of sufficiently sustained decreases in inflation, unexpected inflation is negative and inflationary expectations follow a gradual descent. This suggests that professional forecasters adapt their expectations in line with past movements of inflation. This is particularly striking during the last phases of Volcker’s disinflation in the first part of the 1980s. During the entire sample period more than half of the time unexpected inflation is negative. Such periods are highlighted by means of red vertical and horizontal lines.2
Figure 1 Actual versus expected inflation and unexpected inflation
A test of the hypothesis that expectations are backward looking within a persistent-transitory confusion framework
A natural way to test whether expectations in the US Survey of Professional Forecasters are backward-looking is to specify a stochastic process that is composed of more and less persistent components, none of which is ever observed separately, for actual inflation, derive the optimal predictor of future inflation and fit it to the inflationary expectations data series. After some preliminary experimentation, I settled on a process composed of a first-order Markov process, a white noise process and a constant for actual inflation. The corresponding optimal predictor of future inflation is a distributed lag on actual past inflation plus a constant. The speed of learning implied by the optimal predictor depends on the ratio of the variance of the innovation to the first-order Markov component to the variance of the white noise process, on the coefficient of correlation between current and past inflation and on the constant.
Fitting of this optimal predictor to the one year ahead inflationary expectations from the US Survey of Professional Forecasters results in an equation in which current expected inflation depends on previous actual and expected inflation plus a constant. All coefficients are significant and the adjusted R-squared is 0.95. In addition, the fact that current expected inflation significantly depends on both past actual and expected inflation supports the conclusion that those expectations are backward-looking.3 Another way to evaluate the fit of the optimal predictor in characterising the behaviour of expectations in the US Survey of Professional Forecasters is to calculate the goodness of fit between the original data and its fitted value based on the optimal predictor. The 0.95 value for the adjusted R-squared suggests that the fit is quite good. This may be labelled as a one step ahead tracking method.
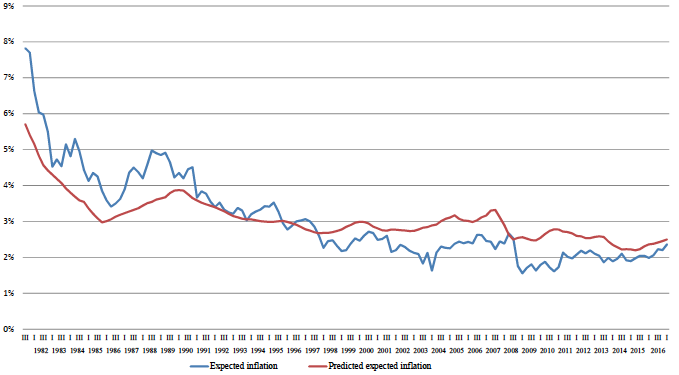
Since one of the regressors in this equation is the lagged value of the original expectation, this is a relatively undemanding measure. Another, more demanding measure, can be obtained by using the estimated equation to generate past inflation instead of using the past survey expectation. Since it utilises the structural dependence of the optimal predictor along with the estimated coefficients on past inflations rather than the original expectation data, the ability of the resulting fitted values to track the behaviour of expectations in the US Survey of Professional Forecasters constitutes a stronger test of the optimal predictor fit. I shall refer to this method as a dynamic tracking method. The actual and dynamic predicted values of expectations in the US Survey of Professional Forecasters are shown in Figure 2. Eyeballing the two curves suggests that the fit of the dynamic tracking method is reasonable. The standard deviation of the difference between the two curves over the entire sample is 0.72%.
Figure 2 Actual and DTM predicted values of SPF expectations
Illustration of the speed of learning implied by the stochastic process fitted to characterise inflationary expectations
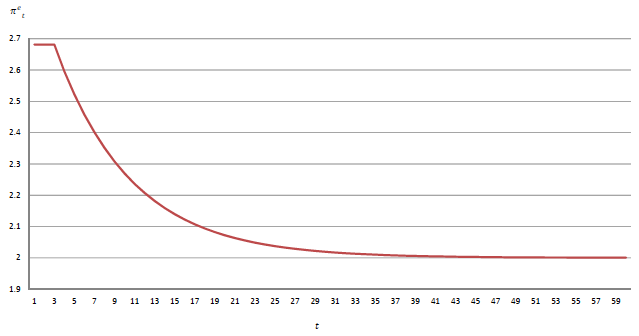
It is convenient to characterise the speed of learning by means of a graph. Figure 3 illustrates the time path it takes to move from the inflationary steady state implied by the estimated optimal predictor to another equilibrium in which inflation is maintained forever at a constant level that permanently maintains expectations at the widely accepted 2% target.4 Applying the steady state definition to the estimated optimal predictor yields an inflationary steady state in which actual and expected inflation are equal to 2.68%. The rate of inflation that would maintain inflationary expectations at the 2% target forever is 1.21%.
Consider now the following thought experiment. Following a sustained period in which actual and expected inflation are both equal to 2.68%, actual inflation goes down unexpectedly to 1.21% and remains there forever. Due to slow learning, this permanent change is perceived only gradually. Figure 3 shows the decrease in expected inflation implied by the estimated optimal predictor as a function of the number of quarters that have elapsed since the downward jump in inflation.
Figure 3 Speed of learning implied by the estimated stochastic process used to characterise SPF inflationary expectations
The figure shows that the estimated process implies a rather slow speed of learning. It takes about ten quarters for expectations to travel halfway between the steady state and the two percent target and about twenty quarters to complete 90% of the adjustment. The first four years at the beginning of the sample during which unexpected inflation is consistently negative (1981-1985 in Figure 1) are roughly consistent with this finding. This supports the view that even when a determined effort to stabilise a gradual inflation is made, as was the case in that period under Volcker, it takes several years for inflationary expectations to fully internalise that this is the case.
References
Clarida, R, J Gali and M Gertler (1999), “The science of monetary policy: A New Keynesian perspective”, Journal of Economic Literature 37(4): 1661-1707.
Cukierman, A (2019), “Implications of the permanent-transitory confusion for New-Keynesian modeling, inflation forecasts and the post-crisis era”, CEPR Discussion Paper 13727.
Friedman, M (1957), A theory of the consumption function, Princeton University Press: Princeton NJ.
Fuhrer, J, and G Moore (1995), “Inflation persistence”, Quarterly Journal of Economics 110(1): 127–159.
Fuhrer, J (1997), "The (un)importance of forward-looking behavior in price specifications", Journal of Money, Credit and Banking 29(3): 338–350.
Gali, J and M Gertler (1999), “Inflation dynamics: A structural econometric analysis”, Journal of Monetary Economics 44(2): 195– 222.
Lucas, R E Jr and L Rapping (1969), “Real wages, employment and inflation”, Journal of Political Economy 77(5): 721-754.
Muth, J F (1960), “Optimal properties of exponentially weighted forecasts”, Journal of the American Statistical Association 55(290): 299-306.
Roberts J. (2001), “How well does the New Keynesian sticky-price model fit the data?”, unpublished manuscript, Board of Governors of the Federal Reserve System.
Steinsson, J (2003), “Optimal monetary policy in an economy with inflation persistence,” Journal of Monetary Economics 50(7): 1425- 1456.
Endnotes
[1] Although this is illustrated within the framework of Clarida et al. (1999), this result is substantially more general, applying to any model in which at least some of the exogenous shocks are subject to either the permanent-transitory confusion or the persistent-transitory confusion.
[2] Since the beginning of the 21st century, fluctuations in actual inflation are less persistent and, in parallel, inflationary expectations are less sensitive to inflationary developments.
[3] The methodology used for the estimation procedure and related details appear in section 4 of Cukierman (2019).
[4] An inflationary steady state is defined as a state in which actual and expected inflation are equal to each other and constant over time. Note that, although they are equal over time, actual and expected inflation are not necessarily equal to each other as is the case in a full steady state.