When the US Federal Reserve finally raised its target for the Federal Funds Rate in December 2015, this likely marked the end of the zero lower bound (ZLB) on short-term nominal interest rates for the US after a staggering seven years. Japan’s ZLB period will most likely exceed this duration under ‘Abenomics’, while the Bank of England similarly has had near-zero interest rates since March of 2009. The ECB is also not expected to raise interest rates for years. Combined with the previous experiences of the ZLB on interest rates that occurred during the Great Depression and in Japan during the 1990s-2000s, this suggests that the two most prominent empirical features of ZLB episodes are that they are rare but long-lived.
The ZLB on interest rates raises a number of profound problems for monetary policymakers, one of which is the traditional question of what the optimal inflation rate should be. While it is well-understood that even stable inflation has costs (such as those arising from price dispersion), higher average inflation is also associated with higher nominal interest rates, which can benefit policymakers by giving them extra room to avoid running into the ZLB. Quantifying the optimal rate of inflation then requires balancing the costs of inflation against its benefits, such as minimising the frequency and severity of ZLB episodes.
But quantifying this potential benefit of higher inflation is difficult because the paucity of ZLB episodes makes their frequency and duration hard to gauge. For example, Schmidt-Grohe and Uribe (2010) calibrated their model prior to the start of the Great Recession and had no post-WWII ZLB episodes in the US to guide their choice over the frequency of hitting the ZLB. The resulting ZLB episodes from their calibration were very rare and short-lived, since violating the zero bound required the nominal interest rate to fall more than 4 standard deviations below its target level. They concluded that the optimal rate of inflation was close to zero. Other pre-Great Recession studies also discussed the ZLB on nominal interest rates as a potential reason for positive inflation but generally considered the ZLB to be such an improbable event as to have little quantitative impact on optimal inflation rates.
The pervasiveness of the ZLB during and since the Great Recession has provided new, but changing, evidence on ZLB durations and frequencies. Coibion et al. (2012) used the fact that the US had spent three years at the ZLB at the time of their writing out of the post-WWII period to fix their frequency, yielding more frequent but still mostly short-lived episodes. These authors conclude that the optimal rate of inflation is unlikely to be much above 2% despite the ZLB on interest rates. But given that actual durations of the most recent ZLB experienced by developed economies continued to rise for several years, previous studies likely underestimated the average duration of ZLB episodes, and therefore the potential benefits of higher levels of target inflation on the part of central banks.
In a recent paper, we revisit the question of the optimal inflation rate in light of longer-lived ZLB episodes (Dordal-i-Carreras et al. 2016). To generate an empirically realistic distribution of ZLB episodes, we integrate an alternative modelling strategy for the shocks that drive the economy into the ZLB (the typical approach generates an excessive proportion of very short-lived episodes) into an otherwise standard New Keynesian model. Each period risk premiums, a shock used to push a model economy into the ZLB, follow a regime-switching process. When the economy is not at the ZLB, there is a fixed probability that the risk premium will rise for a set number of periods. If the increase in the premium is large enough, this shock can generate a very long-lived ZLB episode, although offsetting shocks can end ZLB periods even when risk premiums remain high. Using this framework, we can assess whether (or how much) raising the rate of inflation is optimal, in a welfare sense, to offset the presence of the zero bound on interest rates, since long-lived ZLB episodes generate particularly large welfare costs, which higher levels of steady state inflation can help avoid by reducing their frequency.
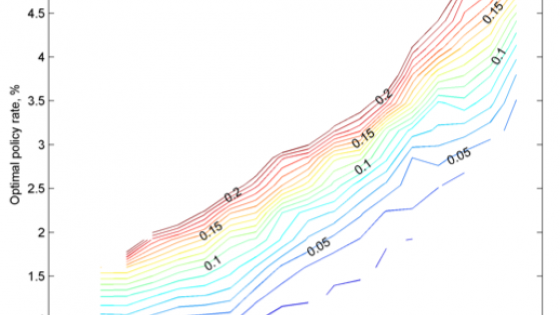
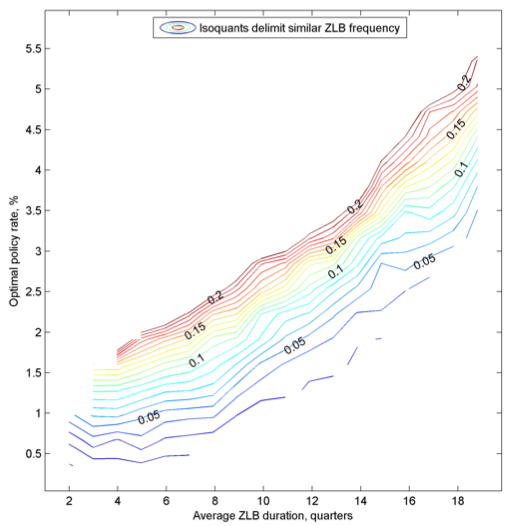
Figure 1 plots the optimal inflation rates (vertical axis) from the model associated with different average durations of ZLB episodes (horizontal axis) and unconditional frequencies of the ZLB (captured by isoquants), where the latter two are measured at a 3.5% steady state inflation rate (historical average for the US). As the average duration of ZLB episodes increases, for a given frequency of being at the ZLB, the optimal inflation rate rises, approximately 1% for every extra year in the average duration of ZLB episodes. The optimal inflation rate is also increasing in the frequency of ZLB episodes, approximately 0.25-0.5% for every additional 5% of time spent at the ZLB. Taking a stand on the optimal rate of inflation therefore requires a good sense of what the historical frequencies and durations of the ZLB are.
Figure 1. Optimal inflation for different frequencies and durations of ZLB episodes
Note: The figure plots the optimal annualised inflation rate (y-axis) associated with different levels of average ZLB durations (x-axis) and unconditional frequencies of the ZLB (indicated by isoquants) for regime switching risk premiums (probability of entering ZLB and duration of elevated risk are varied to change the average durations of ZLB episodes).
Using data from all advanced economies since 1950, we estimate an average frequency of being at the ZLB to be 7.5% and an average duration of ZLB episodes to be three and a half years. Given Figure 1, these magnitudes imply an optimal inflation rate of 2.5-3% per year. However, the estimated frequencies and durations are quite sensitive to individual country experiences. For example, excluding Japan reduces the frequency and duration to 6% and just under three years respectively, lowering the optimal rate of inflation to 2% per year. Excluding the period 1968-1984 when inflation and nominal interest rates were too high for the ZLB to be practically reached, on the other hand, raises the estimated frequency and duration of ZLB episodes to 10% and four and half years respectively, thereby raising the optimal inflation rate to almost 4% per year, the level advocated by economists like Olivier Blanchard and Paul Krugman.
In summary, the specific optimal rate of inflation implied by the model remains very sensitive to one’s beliefs about the frequency and duration of ZLB episodes, values for which history provides only limited guidance. Given the uncertainty associated with measuring historical frequencies and durations of ZLB episodes, the wide range of plausible outcomes that can be reached for the optimal inflation rate implies that profound humility is called for by anyone advocating a specific inflation target.
References
Coibion, O, Y Gorodnichenko, and J Wieland (2012), "The optimal inflation rate in New Keynesian models", Review of Economic Studies 79, 1371-1406.
Dordal-i-Carreras, M, O Coibion, Y Gorodnichenko, and J Wieland (2016), “Infrequent but Long-Lived Zero-Bound Episodes and the Optimal Rate of Inflation”, Annual Review of Economics 8(1).
Schmitt-Grohé, S, and M Uribe (2010), "The Optimal Rate of Inflation", in B M Friedman and M Woodford (eds.), Handbook of Monetary Economics, 1 (3), chapter 13, 653-722, Elsevier.