One of the fundamental challenges in economics is to explain what causes the large cross-country differences in the level of income per capita. Development accounting – which has become the standard approach to address this question – typically assumes a production function for total value added (GDP) and backs out aggregate productivity differences as a residual. That is, aggregate productivity differences are computed as the unobserved factor that explains the cross-country variation in income per capita left unexplained by variation in the physical production factors. Typically, studies within this approach find that around 50% of the variation in per capita income is due to aggregate productivity differences.
Of course, such an aggregate approach leaves open the question about the micro determinants of the observed differences in aggregate productivity. These include within-sector distortions (e.g., due to market power or differential access to finance - see Hsieh and Klenow 2009), sector-specific productivity differences (in particular, low agricultural productivity levels in developing countries – see Gollin et al. 2013), and cross-country differences in input-output (IO) structure interacting with sectoral productivity differences or distortions. In particular, an old literature in development economics has long emphasised the role of IO linkages for aggregate economic performance (e.g. Hirschman 1958) and recently this insight has received new attention by mainstream macroeconomists.
Why do linkages across sectors make a difference for how sector-specific productivity shocks or distortions propagate to the aggregate level? Consider, for example, a productivity increase in the transport sector. This reduces the price of transport services and thereby increases productivity in sectors that use transport services as an input (e.g. mining). Increased productivity in mining in turn increases productivity of the steel sector by reducing the price of iron ore, which in turn increases the productivity of the transport equipment sector. In a second-round effect, this productivity increase improves productivity of the transport sector and so on. Thus, IO linkages between sectors lead to multiplier effects. The IO multiplier of a given sector summarises all these intermediate effects and measures by how much aggregate income will change if productivity of this sector changes by 1%. The size of the sectoral IO multiplier depends mostly on the number of sectors to which a given sector supplies and the intensity with which its output is used as an input by the other sectors1.
Two recent papers on linkages and aggregate productivity differences (Ciccone 2002, Jones 2011) emphasise that IO multipliers and complementarities between inputs of different sectors can in principle amplify relatively small sectoral productivity differences and lead to large aggregate productivity differences across countries. They make this point in a purely theoretical context. On the empirical front, Bartelme and Gorodnichenko (2015) collect IO tables for many countries and time periods and show that countries’ average IO multipliers are positively correlated with aggregate productivity.
In a new empirical study (Fadinger et al. 2016), we complement the existing literature by investigating how differences in the distribution of sectoral IO multipliers, capturing differences in IO structure across countries, interact with sectoral productivities to determine cross-country differences in aggregate income. To this end, we combine data from the World Input-Output Database (Timmer 2012) and the Global Trade Analysis project (GTAP Version 6), and construct a unique dataset of IO tables and sectoral total factor productivities (TFPs) for a large cross section of countries in the year 20052.
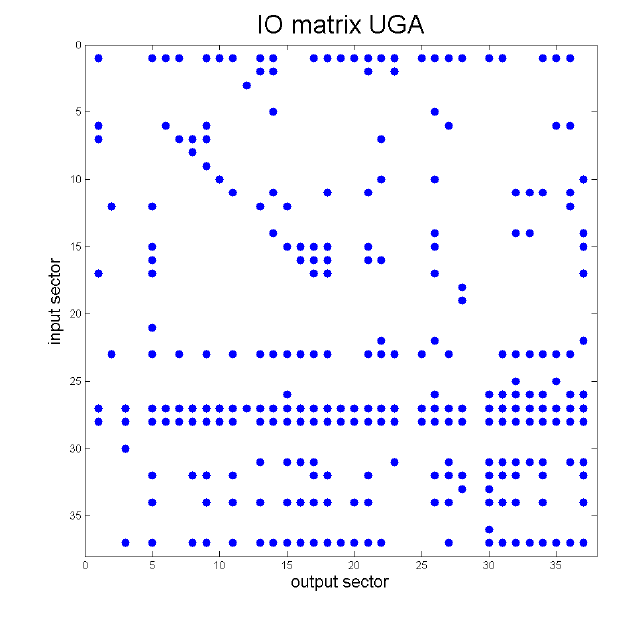
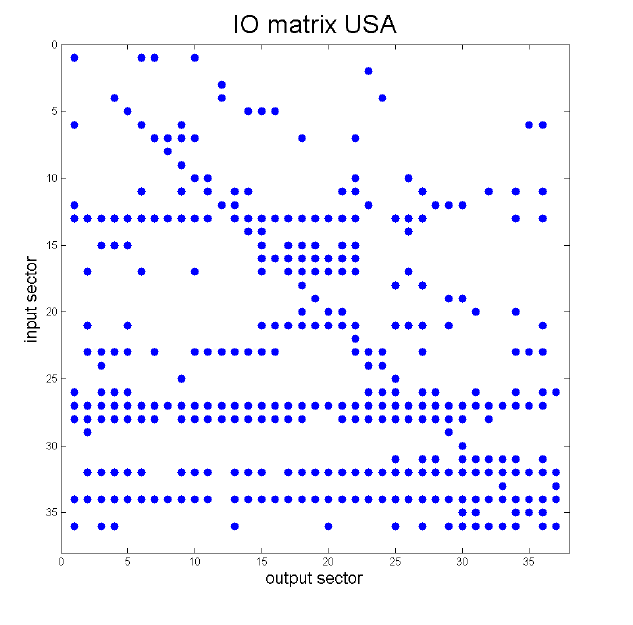
We document substantial differences in the structure of IO linkages between poor and rich economies. Although in all countries there is a relatively small number of sectors with large IO multipliers (the performance of which therefore crucially affects aggregate outcomes), low-income countries typically have a large number of sectors with very low multipliers and only relatively few sectors with intermediate multipliers, while high-income countries have a denser input-output network. To visualise these differences, in Figure 1 we plot a graphical representation of the IO matrices of two countries: Uganda (per capita GDP of $964 PPP in 2005) and the US (per capita GDP of $42,500 PPP in 2005). The columns of the IO matrix are the producing sectors, while the rows are the sectors whose output is used as an input. A dot in the matrix indicates that the column sector uses some of the row sector's output as an input and a blank space indicates that there is no significant connection between the two sectors.
Figure 1. IO matrices of Uganda vs. USA
By comparing the matrices, it is apparent that in Uganda there are only four sectors that supply to most other sectors (Agriculture row 1, Electricity in row 23), Wholesale and Retail Trade in row 27), and Transport in row 28). These sectors are the high-IO-multiplier sectors, where a change in sectoral productivity has a relatively large effect on aggregate output. Most other sectors are quite isolated in Uganda, in the sense that their output is not used as an input by many sectors. By contrast, the US has a significantly larger number of sectors that supply to many others: Chemicals (row 13), Electricity (row 23), Construction (row 26), (Wholesale and Retail) Trade (row 27), Transport (row 28), Financial Services (row 32), and Business Services (row 34), among others.
To study the role of these observed structural differences for aggregate income, we develop and analytically solve a multi-sector general equilibrium model with IO linkages and sector-specific productivities. We then estimate this model using a statistical approach that employs the moments of the distributions instead of actual values. The crucial advantage of this strategy is that it allows us to derive a simple closed-form expression for aggregate per capita income that conveniently summarises the interactions between IO structure and sectoral productivities, without having to deal with the complicated IO matrices directly. Aggregate income is a simple function of the first and second moments of the distribution of IO multipliers and sectoral productivities. From this expression, it follows that income per capita increases in average IO multipliers and average sectoral productivities. Moreover, it is larger when the correlation between sectoral IO multipliers and productivities is positive. The latter reflects the intuition that high sectoral productivities have a larger positive impact if they occur in high-multiplier sectors.
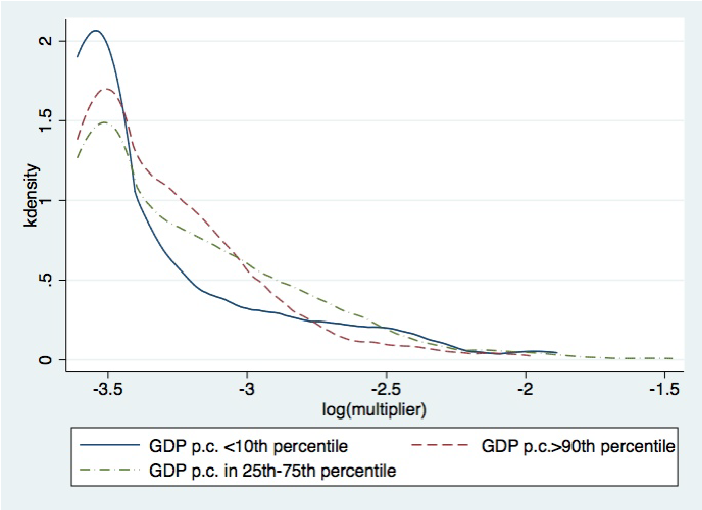
We estimate the parameters of the model to fit the joint empirical distribution of IO multipliers and productivities for the countries in our sample. In line with our earlier observation, we find that low-income countries have more extreme distributions of IO multipliers. While most sectors have very low multipliers, there are a few very high-multiplier sectors. In contrast, rich countries have relatively more sectors with intermediate multipliers (see Figure 2). Moreover, while sectoral IO multipliers and productivities are positively correlated in low-income countries, they are negatively correlated in high-income ones.
Figure 2. Multipliers across rich and poor countries
With these parameter estimates in hand, we use our closed-form expression for income per capita as a function of the moments of the joint distribution of IO multipliers and productivities to predict income differences across countries. We also compare our model with two simpler alternatives: a ‘naïve model’, which only allows for differences in capital per worker but abstracts from any productivity differences across countries, and a model without IO structure, which just averages sectoral productivities but abstracts from linkages between sectors.
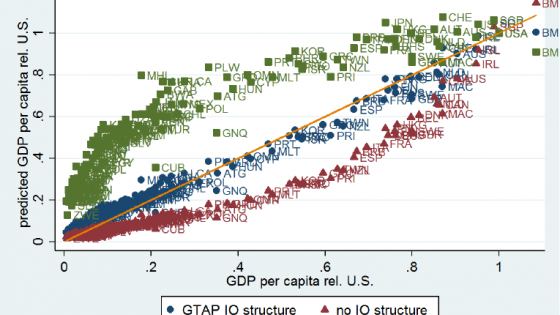
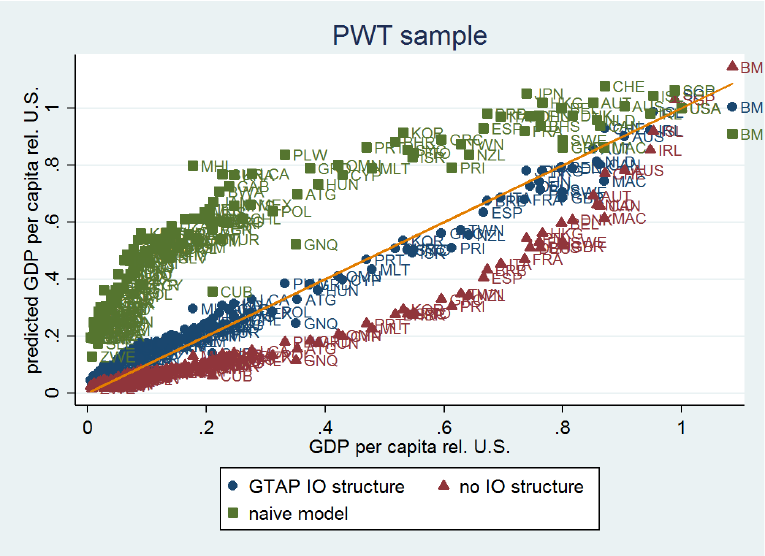
Our findings are demonstrated by Figure 3, which plots predicted income levels (relative to those of the US) against actual income differences for the three models using the Penn World Tables sample (of 155 countries). Our model with IO linkages predicts cross-country income differences extremely well, explaining up to 98% of the cross-country variation in relative income per capita. This is very large compared to standard development accounting exercises (which explain around 50% of this variation – see the naïve model). Moreover, it also does significantly better in terms of predicting income differences than the model that just averages estimated sectoral productivities and ignores IO structure. In fact, this model predicts too large cross-country income differences. The reason is that the big sectoral TFP differences that we observe in the data are to some extent mitigated by countries' IO structures, since low-productivity sectors in low- and middle-income countries tend to be isolated. Thus, if we measured aggregate productivity levels by just averaging sectoral productivities, income levels of low- and middle-income countries would be significantly lower than they actually are.
Figure 3. Predicted income levels vs. actual income differences
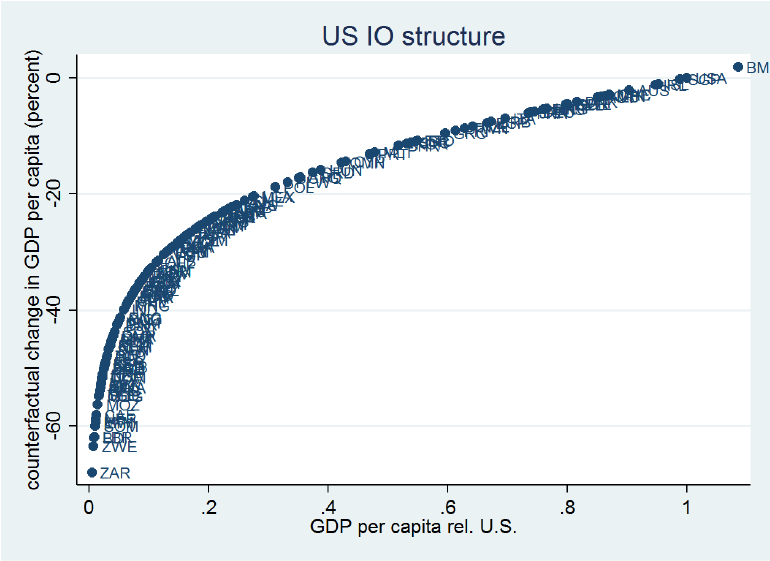
Finally, we perform a number of counterfactuals. For example, we impose the IO structure of the US on all countries, which forces them to use the relatively dense US IO network. We find that this would significantly reduce the income of low- and middle-income countries. For a country at 40% of the US income level (e.g. Mexico) per capita income would decline by around 20% and income reductions would amount to up to 60% for the world's poorest economies (e.g. Congo). The intuition for this result is that poor countries tend to have higher-than-average relative productivity levels (relative to those of the US in the same sector) in precisely those sectors that have higher IO multipliers, while their typical sector is quite isolated from the rest of the economy (an important exception is agriculture, which, in low-income countries, has a high IO multiplier and a below-average productivity level). This implies that they do relatively well given their really low productivity levels in many sectors. Consequently, if we impose the much denser IO structure of the US on poor countries – which would make their typical sector much more connected to the rest of the economy – they would be significantly poorer.
Figure 4. US input-output structure
Thus, differences in IO structure between rich and poor countries have an important effect on aggregate income differences, and this, in turn, has implications for policy. In a poor country like Uganda, changes in the productivity of a few crucial sectors can have large effects on aggregate income, while productivity in most sectors does not matter much for aggregate outcomes, because these sectors are isolated. On the other hand, in rich countries, productivity levels of many more sectors have a significant impact on GDP because the IO network is much denser. To some extent this is good news for low-income countries – in those countries policies that focus on just a few crucial sectors can have a large effect on aggregate income, while this is not true for middle-income and rich economies.
Of course, observed IO linkages are an endogenous outcome of firm’s sourcing decisions. These may be affected by implicit tax wedges that change the intensity of intermediate input use. In an extension of our model, we back out these wedges and show that eliminating them would lead to relatively modest income gains for most countries (a similar conclusion is reached by Bartelme and Gorodnichenko 2015). More generally, productivity and IO structure may be simultaneously determined. To see this, consider the fact that firms adapt their sourcing decisions to economic institutions. For example, when the quality of contracting institutions is low, firms may source some inputs in-house that they would otherwise source at arm’s length. Such decisions may reduce observed linkages and may also lower productivity if they prevent firms from sourcing inputs from the most efficient supplier (see Boehm 2016 for a quantitative model with endogenous IO linkages). Similarly, the price level in output markets may also jointly affect firms’ vertical boundaries and their performance (see e.g. Alfaro et al. 2016). While IO tables should in principle measure linkages independently of whether flows occur inside or outside firm boundaries, in practice this is often not the case. In particular, the inputs produced by single-plant firms that are vertically integrated are often not measured. The same applies to service inputs provided within the firm. All these facts make IO tables endogenous to firm boundaries.
In conclusion, economists are just starting to understand how firms’ sourcing decisions, observed IO linkages and productivity differences are connected and much work remains to be done.
References
Alfaro, L, P Conconi, H Fadinger and A F Newman (2016), "Do Prices Determine Vertical Integration?", Review of Economic Studies, 83(3), 855-888.
Bartelme, D, and Y Gorodnichenko (2015), “Linkages and Economic Development”, NBER Working Paper 21251.
Boehm, J (2015), “The Impact of Contract Enforcement Costs on Outsourcing and Aggregate Productivity”, unpublished manuscript.
Ciccone, A (2002), “Input Chains and Industrialization”, Review of Economic Studies, 69 (3), 565-587.
Duarte, M, and D Restuccia (2010), "The Role of the Structural Transformation in Aggregate Productivity," The Quarterly Journal of Economics, 125(1), 129-173.
Fadinger, H, C Ghiglino, and M Teteryatnikova (2016), “Income Differences and Input-Output Structure”, CEPR Discussion Paper No. DP11547.
Gollin, D, D Lagakos, and M Waugh (2013), “Agricultural Productivity Differences across Countries”, American Economic Review, 104(5), 165-170.
Hirschman, A O (1958), The Strategy of Economic Development, New Haven, CT: Yale University.
Hsieh, C-T, and P J Klenow (2009), “Misallocation and Manufacturing TFP in China and India”, Quarterly Journal of Economics, 124 (4), 1403-1448.
Jones, I C (2011a), “Intermediate Goods and Weak Links in the Theory of Economic Development”, American Economic Journal: Macroeconomics, 3 (2), 1-28.
Timmer, M, (2012), “The World Input-Output Database (WIOD): Contents, Sources and Method", WIOD Working Paper No. 1.
Endnotes
[1] The intensity of input use is measured by the IO coefficient, which states the cents spent on that input per dollar of output. There are also higher-order effects that depend on the number and the IO coefficients of the sectors which supply to the sectors that use the initial sector's output as an input.
[2] Data on sectoral TFPs are available for 36 countries and data on IO tables for 65 countries.