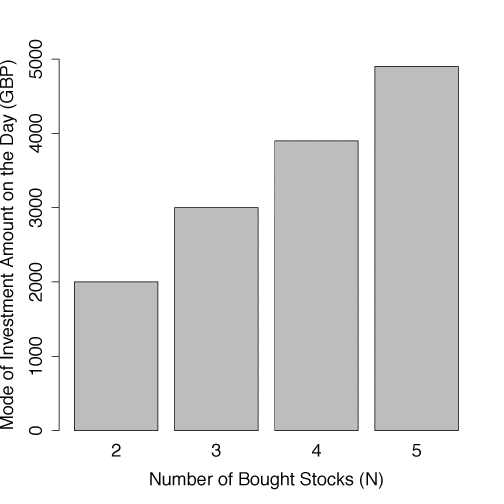The rise of the mutual fund industry and growing number of diversified investment products – such as exchange-traded funds, closed-end funds and unit investment trusts – has provided individual investors with more opportunities than ever to invest in highly diversified, low-cost stock market investments. Yet many choose instead to build a portfolio containing only a few stocks. These investors therefore face the choice of how to diversify over the stocks they hold.
The 1/N heuristic
Portfolio theory guides investors on how to optimally diversify (Markowitz 1952), but in practice most individual investors do not diversify enough (Goetzmann and Kumar 2008).
In our recent work (Gathergood et al. 2019), we analyse how investors who buy individual stocks make diversification choices. We use data from Barclays Stockbroking, a large online broker operating in the UK market. A simple diversification strategy is to equalise portfolio shares across all the stocks held in the portfolio, known as the ‘1/N heuristic’. In theory, this performs roughly as well as other more complicated strategies (DeMiguel et al. 2009). People making a one-shot allocation of pension money across funds often make 1/N allocations (Benartzi and Thaler 2001, Huberman and Jiang 2006).
We show that investors who buy individual stocks often use a simple 1/N diversification rule. They split purchase value equally across stocks bought. When we look at their subsequent behaviour, they do not follow a 1/N heuristic to balance their portfolio shares. Instead, the individual investors apply the 1/N rule only when splitting purchase value across the stocks they buy on a given day.
In other words, they buy 1/N, but they don’t hold 1/N.
For example, an individual following the balanced 1/N portfolio rule would split an investment of £10,000 into equal £5,000 amounts when buying Stock A and Stock B for the first time. Later, the value of the investor’s position in Stock A may have risen to £8,000, and the position in Stock B fallen to £4,000. When investing £10,000 a second time, an investor following a balanced strategy would allocate £3,000 to Stock A and £7,000 to Stock B, creating a balanced portfolio of £11,000 in each stock. We found that investors instead tend to split the second £10,000 equally across the stocks, resulting in a portfolio with £9,000 in Stock A and £13,000 in Stock B.
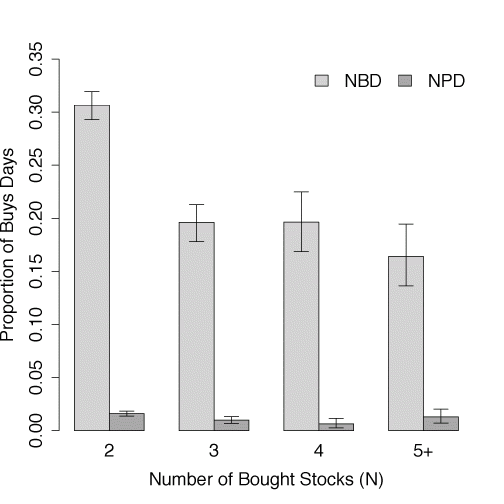
These investors engage in naïve buying diversification (splitting purchase value equally across stocks bought), but not naïve portfolio diversification (splitting purchase value to achieve 1/N portfolio shares). Figure 1 shows, for a sample of all days on which investors purchase more than one stock, that naïve buying diversification is far more common.
Figure 1 Naïve buying diversification and naïve portfolio diversification
Source: Gathergood et al. (2019) based on data from Barclays Stockbroking.
Why does this occur?
This is an example of what economists call narrow framing – the tendency to make choices in isolation rather than making an integrated overall decision. Investors in our sample appear not to be making an overall decision about their portfolio, but instead a narrower decision about how to split purchase values. This challenges existing behavioural finance models of investment choices, which typically model individual investors as trying to optimise an overall portfolio, even though departing from the assumption of strict rationality (for an overview, see Barberis 2018).
It's plausible investors use naïve buying diversification because they have a preference for simplifying the decision problem, and splitting purchase values equally every time you buy stocks is a very simple rule. When we examine the way in which investors implement the rule, there is evidence of a preference for simplicity. The investors commonly choose the denominator and numerator of the 1/N calculation to make the calculation as simple as possible. For example, when investors spend £2,000 they often buy two stocks but rarely three. When investors spend £3,000 they often buy three stocks but rarely two. And when investors spend £4,000 they often buy two stocks but rarely three.
Figure 2 shows this buying behaviour. The figure plots the mode of the total amount invested by the investor in our sample on the day against the number of stocks bought. When investors buy two stocks, the modal amount invested is £2,000. For three stocks, the modal amount invested is £3,000, and so on.
Figure 2 Modal investment amount by number of bought stocks
Source: Gathergood et al. (2019) based on data from Barclays Stockbroking.
These patterns suggest that individuals may not be very concerned about diversification strategies. Maybe individual investors focus on stock-picking – attempting to choose a small collection of stocks that they think will outperform the market. How to diversify may, in their minds, be a secondary issue of much lower importance, and so they tend to employ simplistic diversification rules.
Not portfolio theory
These new results contribute to research that shows that individual investors often make choices at odds with optimal portfolio theory. This highlights a paradox in the behaviour of individual investors. By investing in stocks, some individual investors are smart enough to access the excess returns of the stock market over risk-free investments. Yet, the same individual investors take on excessive risk by holding under-diversified portfolios, and fail to follow a prudent diversification strategy.
References
Barberis, N (2018), "Psychology-based Models of Asset Prices and Trading Volume", Chapter 2 in D Bernheim, S Della Vigna and D Laibson (eds.) Handbook of Behavioral Economics, North Holland.
Benartzi, S and R Thaler (2001), "Naive Diversification Strategies in Defined Contribution Saving Plans", American Economic Review 91: 79–98.
DeMiguel, V, L Garlappi, and R Uppal (2009), "Optimal Versus Naive Diversification: How Inefficient is the 1/N Portfolio Strategy?" Review of Financial Studies 22: 1915–1953.
Gathergood, J, D Hirshleifer, D Leake, H Sakaguchi and N Stewart (2019), "Naïve Buying Diversification and Narrow Framing by Individual Investors", NBER working paper 25567.
Goetzmann, W N and A Kumar (2008), "Equity Portfolio Diversification", Review of Finance 12: 433–463.
Markowitz, H (1952), "Portfolio Selection", Journal of Finance 7: 77–91.