“A growing number of economists say that the government should shift its approach to measuring growth. The current system emphasises data on spending, but the bureau also collects data on income. In theory the two should match perfectly – a penny spent is a penny earned by someone else. But estimates of the two measures can diverge widely, particularly in the short term...”
[Binyamin Appelbaum, The New York Times, 16 August 2011]
Measurement of aggregate real output (GDP) is arguably the most important data collection task. It is a staple in empirical work from vector autoregressions to regime-switching models. It is invariably a key variable used in estimating Dynamic Stochastic General Equilibrium models. Despite its quarterly frequency and the large amount of other data released at higher frequency, it plays a key role in shaping the views and decisions of policymakers as well as the general public. It will come as a surprise to many that significant uncertainty still surrounds its measurement.1 In the US, in particular, two often-divergent GDP estimates exist: a widely used expenditure-side version, and a much less well-known income-side version; we call the annualised growth rates of these two measures GDPE and GDPI (for additional informative background on the US national accounts, see McCulla and Smith 2007 and Landefeld et al. 2008). These two estimates rarely agree – in fact the difference between the two, the so-called statistical discrepancy, can be as large as 7% in absolute value (at an annual rate). As a stark example, in 2000Q1 GDPE was 1.1% while GDPI was 8.1%, and the very next quarter GDPE was 7.5% while GDPI was 2.2%. Clearly, since they are supposed to measure the same underlying true GDP, one of them was badly wrong each quarter.
Many statistical agencies around the world acknowledge this problem and produce a blend of two (or more) GDP measures to come up with their official release. For example, Australia uses equal weights to combine the expenditure- and income-side GDP measures, as well as a third one based on production (See http://www.abs.gov.au, under Australian National Accounts, Explanatory Notes for Australia). The UK and Germany also adjust their released GDP using information from both the income and expenditure sides (Aruoba et al. 2011). However, the US Bureau of Economic Analysis, the agency in charge of producing the national income and product accounts for the US, uses only GDPE as its headline measure. In fact, GDPI is called gross domestic income and until very recently was buried in one of the last tables in a data release.2
In our paper, “Improving GDP Measurement: A Measurement Error Approach”, we propose and implement a framework for obtaining a new estimate of GDP growth that is a blend of the two individual growth rates (Aruoba et al. 2013).3 We explore numerous variations on the key model, exploring different identifying assumptions. In all of them, GDPI growth – which often diverges markedly from GDPE growth – receives substantial weight in the blend. The latest estimates from our preferred blend, which we call GDPplus, are available on the Federal Reserve Bank of Philadelphia website.
The statistical approach: A dynamic factor model with correlated errors
The starting point of our analysis is the simple fact that both GDPE and GDPI are observations of the same underlying ‘true’ GDP, which also contain measurement errors. Thus, denoting the measurement errors by εtE and εtI, we write
GDPtE= GDPt+εtE
GDPtI= GDPt+εtI
which constitute the measurement equations of the state space representation of a dynamic factor model, where GDP is a latent factor. We also specify a transition equation for GDP that shows how the true GDP evolves over time.
The standard approach in a dynamic factor model would be to assume that the innovations to GDP and the measurement errors are all mutually uncorrelated. However, this is actually not very realistic for our application. First, the measurement errors in GDPE and GDPI are likely positively correlated. There is some overlap in the estimates, with government output and some other areas computed identically. Moreover, the same deflator is used for conversion from nominal to real magnitudes, so any measurement error in the price deflator or the areas of overlap will be perfectly positively correlated across the estimates. Second, the measurement errors in GDPE and GDPI are likely correlated with the innovations to true GDP. Nalewaik (2010) shows that the statistical discrepancy (GDPE minus GDPI) is correlated with the business cycle, implying that at least one of the measurement error innovations is correlated with innovations to true GDP.4 Allowing for the three innovations to be arbitrarily correlated makes the model – and, thus, the true GDP – unidentified.
Identifying assumptions
The identification problem stems from the fact that we can make both true GDP and the measurement errors more volatile, while reducing the covariance between the fundamental shocks and the measurement errors, without changing the distribution of observables. How do we achieve identification? We show that imposing just one restriction on the variance-covariance matrix is enough to achieve identification, and it is easiest to form prior views over the ratio of the variance of latent true GDP over the variance of GDPE. A sizeable negative covariance of the measurement error in GDPE with true GDP – for example if GDPE happened to be smoothed enough that it missed considerable variability in true GDP – could imply that this ratio is greater than unity. However, we doubt that this covariance is so negative, and settled on 0.8 as a reasonable value for our baseline model.
A second approach to solving the identification puzzle is by adding a third measurement equation with a certain structure. In particular, we prove that, when another observable variable is added to the model that loads on true GDP with a measurement error orthogonal to the measurement errors in GDPI and GDPE, we achieve identification. We use the change in the unemployment rate as the third variable, since it is computed from surveys of households, while GDPE and GDPI are largely computed from surveys of businesses or tax records, whose measurement errors are likely to have different properties. As it turns out, the parameter estimates from the two-equation model where we fix the ratio of the variances of true GDP and GDPE are very similar to the parameter estimates from the three-equation model using the change in the unemployment rate. The variance of the measurement error in GDPE is larger than that of the measurement error in GDPI; the measurement errors are positively correlated, as expected; and they are negatively correlated with the innovations to true GDP – with the negative correlation larger for GDPE than for GDPI.5 The Kalman gain is larger for GDPI than for GDPE, so loosely speaking, an innovation to GDPI is more informative for true GDP than is an innovation to GDPE.
Policy implications and recent GDP growth estimates
One notable result from the models is that the variances of the measurement errors are large, so neither individual output growth estimate appears to be very reliable. Policymakers would do well to heed this warning – for any given quarter, either individual output growth estimate could be far from true GDP growth. Going back to the example at the beginning, the values for GDPplus in 2000Q1 and 2000Q2 are 6.5% and 2.9% respectively, which are much less extreme relative to either of the two individual measures and paint a more reliable picture of the slowdown of the US economy, which entered into a mild recession a few quarters later.
Another key message from the results is that shocks to GDP growth are likely more persistent than is commonly believed. The first-order autocorrelation (AR1) parameter for GDPE growth is only 0.3, but the AR1 estimate for true GDP growth from our benchmark two-equation model is double that – about 0.6. An AR1 of 0.6 is also what one finds for the change in the unemployment rate, suggesting a common level of persistence to shocks to the US economy that is masked by considerable measurement error in GDPE growth. Estimating a two-state Markov switching model, we find even higher GDP growth persistence in low-growth states (typically recessions and low-growth periods around recessions), where the estimated AR1 parameter is around 0.8.
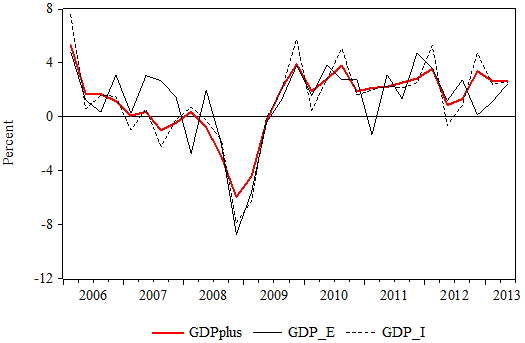
What do the latest GDPplus estimates say about the state of recent economic growth? The time series plot of GDPplus is available on website at the Federal Reserve Bank of Philadelphia. In Figure 1, we plot GDPplus along with GDPE and GDPI growth rates for the period 2006Q1–2013Q2, which encompasses the Great Recession.
Figure 1. Measures of US GDP, 2006Q1–2013Q2
First, over the recovery starting in the third quarter of 2009, GDPplus is considerably less volatile than either GDPE or GDPI – suggesting that much of the recent variation in the individual estimates has been noise.6 Second, the GDPplus estimates imply a slightly faster pace of growth over the recovery than is commonly believed – around 2.6% per year, versus around 2.25% for GDPE.7 Furthermore, the current GDPE data indicates that the US economy has stumbled badly over the past year, with average growth of only around 1.6% over the four quarters through the third quarter of 2013 – down markedly from its average pace over the previous four quarters. In contrast, GDPplus grew at a pace of about 2.9% over the four quarters through the third quarter of 2013 – not far from its average growth rate over the whole recovery. In other words, most of the deceleration is GDPE over the past year appears to be a figment – pure measurement error sending an overly pessimistic signal about the pace of economic growth. It is likely closer to the truth that the US economy has continued to chug along over the past year (as it has through most of the recovery), at a pace that has been modest but fast enough to provide steady and sustained job growth and unemployment rate declines. While this is not an entirely inspiring situation, it is less downbeat than the noisy GDPE estimates currently suggest.
References
Aruoba, S Borağan, Francis X Diebold, Jeremy J Nalewaik, Frank Schorfheide, and Dongho Song (2013), “Improving GDP Measurement: A Measurement-Error Perspective”, Federal Reserve Bank of Philadelphia Working Paper No. 13-16, 2 May.
Barker, van der Ploeg, and Weale (1984), “A Balanced System of National Accounts for the United Kingdom”, Review of Income and Wealth, 461–485.
Beaulieu, J and E J Bartelsman (2004), “Integrating Expenditure and Income Data: What To Do With the Statistical Discrepancy?”, manuscript, Federal Reserve Board.
Byron, R (1978), “The Estimation of Large Social Accounts Matrices”, Journal of the Royal Statistical Society Series A, 141(3): 359–367.
Byron, R (1996), “Diagnostic Testing and Sensitivity Analysis in the Construction of Social Accounting Matrices”, Journal of the Royal Statistical Society Series A, 159(1): 133–148.
Chen, B (2012), “A Balanced System of U.S. Industry Accounts and the Distribution of the Aggregate Statistical Discrepancy by Industry”, Journal of Business and Economic Statistics, 30: 202–211.
Fixler, D J and J J Nalewaik (2009), “News, Noise, and Estimates of the ‘True’ Unobserved State of the Economy”, manuscript, Bureau of Economic Analysis and Federal Reserve Board.
Fleischman, C A and J M Roberts (2011), “A Multivariate Estimate of Trends and Cycles”, manuscript, Federal Reserve Board.
Landefeld, J S, E P Seskin, and B M Fraumeni (2008), “Taking the Pulse of the Economy: Measuring GDP”, Journal of Economic Perspectives, 22: 193–216.
McCulla, S H and S Smith (2007), “Measuring the Economy: A Primer on GDP and the National Income and Product Accounts”, Bureau of Economic Analysis.
Nalewaik, J J (2010), “The Income- and Expenditure-Side Estimates of U.S. Output Growth”, Brookings Papers on Economic Activity, 1: 71–127 (with discussion).
Rassier, D G (2012), “The Role of Profits and Income in the Statistical Discrepancy," Survey of Current Business: 8–22.
Solomou, S and M Weale (1991), “Balanced Estimates of U.K. GDP 1870–1913”, Explorations in Economic History, 28: 54–63.
Solomou, S and M Weale (1993), “Balanced Estimates of National Accounts When Measurement Errors Are Autocorrelated: The U.K., 1920–1938”, Journal of the Royal Statistical Society Series A, 156(1): 89–105.
Stone, R, D G Champernowne, and J E Meade (1942), “The Precision of National Income Estimates”, Review of Economic Studies, 9: 111–125.
Weale, M (1985), “Testing Linear Hypotheses on National Accounts Data”, Review of Economics and Statistics, 90: 685–689.
Weale, M (1988), “The Reconciliation of Values, Volumes, and Prices in the National Accounts”, Journal of the Royal Statistical Society Series A, 151(1): 211–221.
1 Aruoba (2008) reports that the difference between the initial announcement and the final-revised value for annualised quarterly expenditure-side estimates of GDP growth fluctuates between -3.4% and 6.6%, with a standard deviation of 1.7%.
2 The annualised growth rates we discuss here can be found online in the Bureau of Economic Analysis National Income and Product Accounts interactive tables, Table 1.7.1.
3 For related work in this area, see Fleischman and Roberts (2011), as well as the literature on ‘balancing’ the national income accounts. This literature extends back to Stone et al. (1942), and subsequent work includes Byron (1978), Barker et al. (1984), Weale (1985), Weale (1988), Solomou and Weale (1991, 1993), Byron (1996), Beaulieu and Bartelsman (2004), and Chen (2012).
4 Fixler and Nalewaik (2009) arrive at the same result using evidence from GDPE and GDPI revisions to show that the idiosyncratic variation in the estimates is likely correlated with true GDP.
5 Some economists at the Bureau of Economic Analysis have suggested that GDPI is too cyclical because capital gains might be leaking into the estimates, and capital gains are likely positively correlated with output growth (see Rassier 2012). If this were the case, we would expect the measurement error in GDPI to have positive covariance with the innovations to true GDP – the opposite of what we find in the three-equation model. In the two-equation model, such positive covariance, if sizeable, would be consistent with a low ratio of the variance of latent true GDP over the variance of GDPE, implying that much of the variance of GDPE is noise.
6 The standard deviation of GDPplus over the recovery is about half the standard deviation of either GDPE or GDPI.
7 Note that the GDPE and GDPI estimates are subject to large revisions (larger revisions than many other widely-followed indicators like the unemployment rate and payroll employment), so the numbers written down in this note may differ from the official estimates as they appear years and decades from now.