There has recently been much media comment, academic discussion and policy debate devoted to the observation that in many economies, the relationship between inflation and economic slack – the Phillips curve – appears to have weakened or even disappeared.1 Some papers have estimated that the slope of the Phillips curve has flattened over time (Ball and Mazumder 2011, IMF 2013, Blanchard et al. 2015).Others have shown that inflation can be well-approximated and forecast by statistical processes unrelated to the amount of slack (Atkeson and Ohanian 2001, Stock and Watson 2007, 2009, Dotsey, et al. 2017, Cecchetti et al. 2017, Forbes et al. 2017).
On the face of it, these findings could have major implications for monetary policy. The Phillips curve is one of the building blocks of the standard macroeconomic models used for forecasting and policy advice in central banks. A breakdown in the relationship would challenge the wisdom of these models and the usefulness of their forecasts. Arguably, it would call in to question part of the rationale for independent, inflation-targeting central banks. In a recent paper (McLeay and Tenreyro, 2018), we argue that such fears may be misplaced.
Successful monetary policy should hide the empirical Phillips curve
We use a standard conceptual framework (Clarida et al.1999; although similar results would obtain in the classic setting of Barro and Gordon 1983) to show why:
- the empirical disconnect between inflation and slack is exactly what one should expect when monetary policy is set optimally; and
- the result is perfectly consistent with an underlying stable and positively sloped Phillips curve.
Specifically, in our paper the Phillips curve always holds – inflation depends positively on the output gap by assumption. Cost-push shocks can lead to deviations from the curve, but do not alter its slope. But we also assume that monetary policy is set optimally under discretion to maximise welfare, captured by objectives to eliminate slack and stabilise inflation (in line with typical central bank mandates). Given these objectives, good monetary policy will typically seek to eliminate any developing output gaps in order to stabilise inflation at its target. When faced with cost-push shocks it should aim to strike a balance between the two goals. In either case, the central bank’s actions seek to reduce output whenever inflation is set to rise above target. This targeting rule imparts a negative correlation between inflation and the output gap, blurring the identification of the (positively sloped) Phillips curve.
If the central bank is successful in achieving its objectives, then equilibrium inflation will completely inherit the statistical properties of the cost-push shocks affecting the Phillips curve. This is entirely in line with recent empirical results in Cecchetti et al. (2017) and Forbes et al. (2017), which suggest that inflation data in the US and the UK can be modelled as an exogenous statistical process, unrelated to measures of slack. It is also consistent with the findings in large-scale models such as Smets and Wouters (2007) that mark-up shocks can explain much of the variation in inflation. This is exactly what one should expect to see under successful, systematic monetary policy.
The identification problem
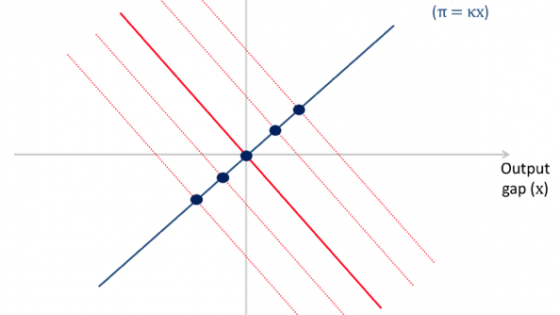
In our stylised setting, recovering the Phillips curve from the data leads to a classical identification problem. Figure 1 plots the Phillips curve in the model (in blue), alongside the monetary policy targeting rule (in red). In equilibrium we do not observe the Phillips curve, but rather the intersection between the two lines. The situation is analogous to the textbook case of simultaneously determined supply and demand curves.
A naïve econometrician running simple OLS regressions will fail to recover the Phillips curve. Indeed, when the Phillips curve is subject to cost-push shocks and when monetary policy perfectly offsets shocks to demand, the data will perfectly trace out the negatively sloped targeting rule, rather than the positively sloped Phillips curve.
Figure 1 Phillips curve and optimal monetary policy with cost-push shocks
Source: McLeay and Tenreyro (2018).
Recovering the Phillips curve
Successful monetary policy will make the Phillips curve harder to see in the data. But it is crucial for monetary policymakers to know whether the underlying Phillips curve is still present (but hidden), or if it has actually disappeared. There are a number of possible solutions to the identification challenge.
1) Shocks to the monetary policy targeting rule (arising from policy errors, lags or changes in policymaker preferences) can help recover the Phillips curve
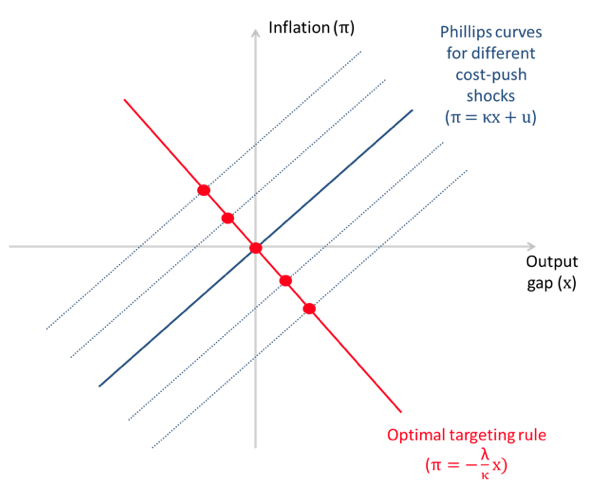
We show how the observed inflation-output gap relationship depends on the relative variance of cost-push and targeting-rule shocks. If the latter are dominant, the identified parameter will be closer to the true slope of the Phillips curve. Shocks to the targeting rule shift the equilibrium along the Phillips curve, rather than shifting the curve itself (Figure 2). If the variance of the targeting-rule shocks is high enough, then successfully controlling for cost-push shocks such as changes in oil prices should help the econometrician to recover the Phillips curve using standard OLS techniques. The vast VAR literature on the identification of exogenous monetary policy shocks (and their effects on output and inflation) offers an alternative way of distilling the structural Phillips curve relationship.
Figure 2 Phillips curve and optimal monetary policy with targeting-rule shocks
Source: McLeay and Tenreyro (2018).
2) Finding suitable instruments
In our standard framework, the optimal commitment policy involves a greater degree of inertia in the equilibrium outturns for inflation and the output gap. Using lagged observations of the output gap as instruments can therefore recover the underlying Phillips curve. In reality, finding good instruments may be more challenging, not least because monetary policymakers do not typically set time inconsistent policies in practice.
3) Identifying the wage Phillips curve
Wage inflation is one step removed from the price inflation targets of most central banks, so the identification issue may be smaller for wage Phillips curves. When a shock drives a wedge between the two inflation measures, monetary policy should only seek to attenuate its impact on price inflation. All else equal, the original Phillips (1958) correlation between wage inflation and unemployment may therefore be less affected by endogenous monetary policy actions.
4) Disaggregated Phillips curves
A final possible solution is to take advantage of more disaggregated data. Monetary policy mandates require central banks to respond to aggregate measures of inflation and slack. If there are idiosyncratic movements in slack at more disaggregated regional or sectoral levels, then monetary policy will only offset them to the extent they affect those aggregates. If there is enough cross-sectional variation, econometricians may be able to use it to recover the aggregate Phillips curve.
Conclusion
We have long known that the empirical Phillips curve may vary with monetary policy (Lucas 1976). One common explanation for the Great Inflation of the 1970s is that policymakers mistakenly tried to exploit the prevailing reduced-form Phillips curve, and in so doing caused it to disappear (e.g. Sargent et al. 2006). In contrast, our point is that a disappearing Phillips curve is also a natural consequence of good monetary policy. If the true model of the economy involves a Phillips curve relationship, monetary policymakers aware of its existence should ensure it remains elusive in the data.
Authors’ note: The views expressed in this column are those of the authors and not necessarily those of the Bank of England.
References
Atkeson, A and L E Ohanian (2001), “Are Phillips curves useful for forecasting inflation?” Federal Reserve Bank of Minneapolis Quarterly Review 25(1): 2.
Ball, L, and S Mazumder (2011), “Inflation Dynamics and the Great Recession.” Brookings Papers on Economic Activity 42(1): 337–405.
Barro, R J, and D B Gordon (1983), “A positive theory of monetary policy in a natural rate model.” Journal of Political Economy 91(4): 589–610.
Blanchard, O, E Cerutti, and L Summers (2015), “Inflation and activity–Two explorations and their monetary policy implications.” NBER Working Paper 21726.
Cecchetti, S G, M Feroli, P Hooper, A K Kashyap, and K L Schoenholtz (2017), “Deflating Inflation Expectations: the Implications of Inflation’s Simple Dynamics.” CEPR Discussion Paper 11925.
Clarida, R, J Galí, and M Gertler (1999), “The science of monetary policy: a new Keynesian perspective.” Journal of Economic Literature 37(4): 1661–1707.
Dotsey, M, S Fujita, and T Stark (2017), “Do Phillips Curves Conditionally Help to Forecast Inflation?” Working Paper 17-26, Federal Reserve Bank of Philadelphia.
Forbes, K, L Kirkham, and K Theodoridis (2017), “A trendy approach to UK inflation dynamics.” Discussion Paper 49, Monetary Policy Committee Unit, Bank of England.
IMF (2013), “The Dog that Didnt Bark: Has Inflation Been Muzzled or Was it Just Sleeping?” World Economic Outlook, IMF, Chapter 3.
Lucas, R E (1976), “Econometric policy evaluation: A critique.” Carnegie-Rochester Conference Series on Public Policy 1: 19 – 46.
McLeay, M and S Tenreyro (2018), “Optimal Inflation and the Identification of the Phillips Curve”, CEPR Discussion Paper 12981.
Phillips, A W (1958), “The relation between unemployment and the rate of change of money wage rates in the United Kingdom, 1861–1957.” Economica 25(100): 283–299.
Sargent, T, N Williams, and T Zha (2006), “Shocks and Government Beliefs: The Rise and Fall of American Inflation.” American Economic Review 96(4): 1193–1224.
Stock, J, and M W Watson (2007), “Why Has U.S. Inflation Become Harder to Forecast?” Journal of Money, Credit and Banking 39(s1): 3–33.
Stock, J, and M W. Watson (2009), “Phillips Curve Inflation Forecasts.” In J Fuhrer, Y Kodrzycki, J Little and G Olivei (eds), Understanding Inflation and the Implications for Monetary Policy, MIT Press, 99–202.
Endnotes
[1] See articles in the Financial Times, Wall Street Journal and The Economist, for example.