Thomas Piketty has recently drawn worldwide attention with the proposition that the disparity between wage earners and capital owners is increasing, and that governments should intervene to bring this process to a standstill.
The popularity of Piketty's book, Capital in the 21st century (2014), is also due to the publication of his comprehensive dataset and the many resources behind those data. Another reason for his popularity is the relative simplicity of the only two formulas in the book, which he named the ‘Fundamental Laws of Capitalism’. However, these simple formulas have their limitations. Piketty neglects a substantial part of economic activity by disregarding investment replacement and depreciation.
I show below what will happen with Piketty's laws when investment replacement is added. I start with the second law, which stands central in the book. References to the relevant pages in the book of Piketty (2014) are in parentheses.
Piketty’s second law
Piketty's thesis that since 1970 wealth has been growing faster than income is based on the observation that the growth rate of income in the nine countries surveyed is decreasing, while the savings rate hardly changes. He calls this the ‘second fundamental law of capitalism’, or formally: β=s/g (p. 166). Here, β is the ratio of wealth and income, known as the capital coefficient. This ratio is positively related to the savings rate s, and negatively to the growth rate of income g. Piketty gives the following example. If the savings rate of 12% does not change, and the growth rate is halved from 4% to 2%, the capital ratio of 300% increases to 600%. This is a formidable rise of the ratio between capital and income, and the strength of Piketty's argument is that he also finds this increase in his data for the period 1970-2010 (p. 26).
It should be noted that the equation β=s/g is not that startling. Every introductory textbook in macroeconomics teaches that the circular flow is in equilibrium if savings equal investment, or sY=gK. Rewriting this equality yields Piketty's second law. The ‘fundamental’ behind this equation is that you need ‘capitalism’ in the form of financial markets to get equilibrium in the circular flow.
A problem with this formulation of the equilibrium condition is that Piketty only looks at net investment, gK. This has important implications for the outcome of the formula, because the capital-output ratio tends to give unlikely high values at low rates of growth. With a growth rate of 1%, for example, and a savings rate of 10%, the capital ratio is 1000%, and if the growth rate goes to zero, the capital coefficient even tends to infinity (p. 228).
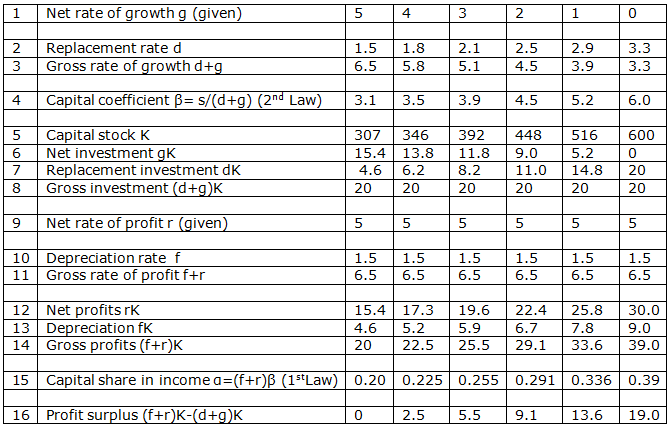
Piketty would not have this problem if he had incorporated investment replacement in the equilibrium condition of the circular flow. This is illustrated in Table 1. This table is based on the reproduction model with fixed capital, which is known from Von Neumann and Sraffa. For my argument, it will suffice to assume that capital goods have a fixed technical lifetime T, and that they suddenly ‘die’ at the end of this period (Van Schaik 1976).
Table 1. Extension of Piketty's Laws of Capitalism: A numerical exercise
Note: The second law (line 4) follows from equilibrium of the circular flow, in which macroeconomic savings equal investment (in symbols, sY =(d + g)K). Here, Y is GDP, and s gross macroeconomic savings rate that has been fixed at 20% in this example. It is assumed that there is no saving from labour income. The lifetime of capital goods is 30 years (sudden death). The first law (line 15) is the definition of the profit ratio. For other values of the savings rate and the life-span of capital conclusions do not change.
Investment replacement
The solution of the model describes the long-term situation of balanced growth. In the table, six growth paths are put next to each other – the first with a growth rate of 5%, and the last with 0% growth (line 1). These are just like in Piketty’s (2014) net growth rates. It can be deduced from the reproduction model that the replacement rate is a function of the growth rate and the life-span of capital goods.1
The replacement rate increases as the growth rate is lower (line 2). The exercise is based on a technical lifetime of 30 years. The further magnitude of T is not essential. With a zero growth rate, the replacement rate equals the reciprocal of the life-span, in this example – 3 ⅓.
The sum of the replacement rate and the net growth rate is the gross rate of growth (line 3). Following Piketty, I assume a given macroeconomic savings rate s, which now also includes depreciation. In equilibrium, gross savings equal gross investment (i.e. sY=(d+g)K). The second fundamental law thus becomes: β=s/(d+g). Assuming a savings rate of 20% (p.178), the capital coefficient is (rounded to) 310% in case of a net growth rate of 5%, and 600% in case of a net growth rate of 0% (line 4). So, at low growth rates, the capital coefficient does not become incredibly high and Piketty's second law actually holds.
The capital stock is a percentage of income (line 5). Therefore, investment is also a percentage of income. In equilibrium, the gross investment rate equals the gross savings rate of 20% (line 8). It is noteworthy that the investment replacement at low growth rates is much larger than the net investment. Thus, since 1970 an increasing part of savings is allocated to replace the capital stock and not to the expansion of the capital stock.
Piketty’s first law
The first law is the definition of capital income ratio: α=rβ (p. 52). Here, r is the net rate of profit, which according Piketty is on average at the 5% level (p. 202), although lower values are not excluded in the future. A capital coefficient of, for example, 600% results in a profit share of 30%. These are the net profits. To determine the gross profits, depreciation should be included. It can be deduced from the reproduction model that the depreciation rate is a function of the rate of profit and the life-span of capital goods (formally, f=r/[(1+r)^T-1]).
Profit ratio
In case of a net profit rate of 5% and a lifetime of 30 years, the depreciation rate is 1.5% (line 10). The sum of the depreciation rate and the net rate of profit is the gross profit rate (line 11). Thus, the first fundamental law can be rewritten as α=(f +r)β. Since the gross profit rate is 6.5% in each steady state, there is a clear negative relationship between the capital share in income and economic growth (line 14). At ever lower rates of growth, the ratio between wealth and income increases, so that profits are correspondingly higher. In the example, the profit ratio increases from 20% at a growth rate of 5%, to 39% at a growth rate of 0%. These figures are not unrealistic when we look at Piketty's data (p. 222).
This is also an explanation for the structural decline in the labour share of income. From 1970 onwards, the old industrialised countries have arrived on a lower growth path. This has led to an increase in the ratio between capital and income (the second law), which at an unchanged rate of profit has increased the share of profits in income (the first law).
Surplus profits
In the example, I assume that there is no saving from labour income – the savings come entirely from profits. The table shows that profits rise as growth is lower. In each steady state, macroeconomic savings are 20% of the income. The savings rate exactly equals the capital share in income if he growth rate is equal to the rate of profit (r=g). This is the situation in the Golden Age of the 1950s and 1960s. In the decades that followed, growth rates became lower, while profit rates remained high. That is why a surplus of profits has arisen. With a growth rate of 2% this surplus is approximately 9% of the income (line 16).
This explains, for example, why countries with a marked slowdown in economic growth, such as the Netherlands and Japan, have been confronted which huge surpluses in the current account of the balance of payments. In this respect, the expansion of Piketty's laws leads to interesting vistas to broaden the discussion on raising taxes on wealth to taxing surplus profits.
References
Piketty, T (2014), Capital in the Twenty-First Century, London.
Van Schaik, T (1976), Reproduction and fixed capital, Tilburg University Press
Van Schaik, T (2014), “Broaden discussion Piketty's book to taxing profits,” Me Judice, 16 June.
Copyright
The title and first sentences of this article may be reproduced with the citation without permission Me Judice and, if online, a link to the article. Full text is permitted limited. For more information, see our copyright guidelines.
Footnote
1 Formally: d = g/[(1+g)^T-1]