Important events are hard to predict – a fact that is particularly hard-felt when it comes to low probability events with dramatic consequences. Nuclear catastrophe, financial crisis and the like are things that even experts struggle to predict. The difficulty stems from a lack of understanding of the underlying factors and complex interactions among causes (probabilities are not independent but conditional on other events).
Experts are thus to some extent forced to base their predictions on inference from observing the past. A difficult issue is to know when a model should be revised given that an event that has been deemed to be highly improbable happens to occur. The issue is most relevant for policy recommendations. For example, what recommendations should experts provide for the regulation of nuclear power in the wake of the Fukushima disaster or for the regulation of banks in the light of the recent financial crisis?
While experts struggle to predict such events accurately, the average person is often simply baffled. They tend to misperceive randomness in a variety of ways, especially when it comes to rare events.
- One common tendency is to see patterns in random data when there are none.
This can lead to a tendency to overreact to recent events, allowing their occurrence to change beliefs about future events in exaggerated ways. More specifically, many people tend to over-infer characteristics of the underlying probability distribution when observing a small number of random events. A literature pioneered by Tversky and Kahneman (1971) has identified the belief in the “law of small numbers” as the source of such over-inference.
Why do people “over infer” from recent events?
There are two plausible but apparently contradicting intuitions about how people over-infer from observing recent events.
- The “gambler’s fallacy” claims that people expect rapid reversion to the mean.
For example, upon observing three outcomes of “red” in roulette, gamblers tend to think that “black” is now due and tend to bet more on “black” (Croson and Sundali 2005).
- The “hot hand fallacy” claims that upon observing an unusual streak of events, people tend to predict that the streak will continue.
The “hot hand” fallacy term originates from basketball where players who scored several times in row are believed to have a “hot hand”, i.e. are more likely to score at their next attempt (e.g. Camerer 1989).
Recent behavioural theory has proposed a foundation to reconcile the apparent contradiction between the two types of over-inference (Rabin and Vayanos 2010). The intuition behind the theory can be explained with reference to the example of roulette play.
A person believing in the “law of small numbers” thinks that small samples should “look like” the parent distribution, i.e. that the sample should be representative of the parent distribution. Thus, the person believes that out of, say, 6 spins 3 should be red and 3 should be black (ignoring green). If observed outcomes in the small sample differ from the 50:50 ratio, immediate reversal is expected. Thus, somebody observing 2 times red in 6 consecutive spins believes that black is “due” on the 3rd spin to restore the 50:50 ratio.
Now suppose such person is uncertain about the fairness of the roulette wheel. Upon observing an improbable event (6 times red in 6 spins, say), the person starts to doubt about the fairness of the roulette wheel because a long streak does not correspond to what he believes a random sequence should look like. The person then revises his model of the data generating process and starts to believe the event on streak is more likely. The upshot of the theory is that the same person may at first (when the streak is short) believe in reversion of the trend (the gambler’s fallacy) and later – when the streak is long – in continuation of the trend (the hot hand fallacy).
In recent work, we use a unique data set from lotto gambling to confront this theory with the data (Jørgensen et al. 2011). Lotto gambling provides a particularly convincing opportunity to demonstrate biases in prediction.
- The underlying random process is known and every effort is made to make it transparent (the drawing of balls from an urn is aired on TV and subject to government monitoring).
- It should be clear to any observer that lotto numbers are truly random, and that observing past draws provides no information whatsoever about future draws (i.e. draws are truly independent).
The data used in this study is unique because we are able to track individual lotto players over time (Clotfelder and Cook 1993, among others, have used lotto data to study the gambler’s fallacy but these researchers were not able to observe individual choices).
The ability to track individuals over time allows us to study how lotto players react to recent draws. These reactions provide a measure of how lotto players predict future draws based on past observations. We use a large data set from the Danish 7/36 state lotto to investigate whether the gambler’s fallacy and the hot hand fallacy occur in a natural but tightly controlled environment with high stakes, and whether the two biases relate as theorised.
We find evidence for both types of bias and show that the biases are indeed related as hypothesised by Rabin and Vayanos (2010). While most players tend to pick the same numbers week after week no matter what, those who do react tend to react by avoiding numbers drawn in the previous week but tend to favour numbers drawn several weeks in a row. Importantly, the individual-level data allows us to show that the two biases are systematically related. Players who are prone to the gambler’s fallacy also tend to be prone to the hot hand fallacy. While the two biases exist and coexist to some extent (i.e. some players are not prone to either bias, some are prone to only one of the biases, some to both), these biases on the individual level are sufficiently pronounced and systematic that they are also visible in aggregate data.
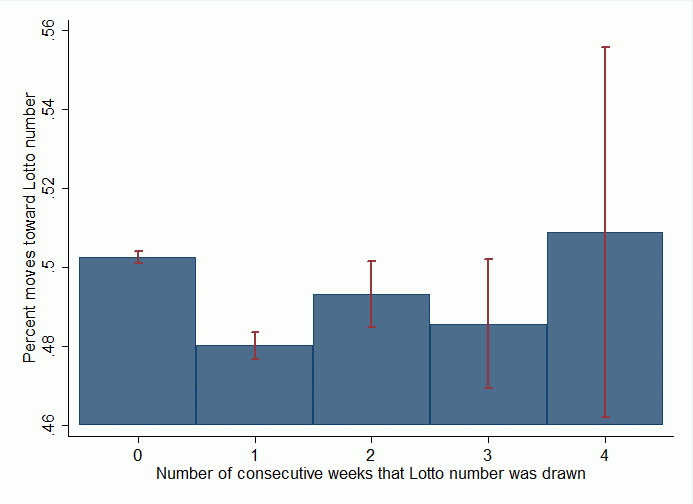
Figure 1 shows the percentage of all reactions (a move toward a lotto number that has been drawn) as a function of the number of consecutive weeks that the lotto number was drawn. For example, the first bar shows that if a particular number was not drawn in the previous week (a likely event) players are relatively indifferent about the number they pick (they are about equally likely to pick the number or not). The second bar shows that if a particular number has been drawn in the previous week it is significantly less likely to be picked (by about 2 percentage points), indicating the presence of the gambler’s fallacy at the aggregate level. The bars further to the right show that as a particular number happens to be drawn several times in a row (an unlikely event) it tends to become increasingly popular compared to the case where the number has been drawn in the previous week only. These results from lotto gambling are in line with recent findings from the experimental laboratory (Asparouhova et al. 2009).
Figure 1: Percentage of moves toward Lotto numbers as a function of number of consecutive weeks that Lotto number was drawn (including 95% confidence intervals)
Costly misperceptions
The belief that winning lotto numbers can be predicted from observing past draws may seem simply absurd, but is such a bias also costly? We find that the answer is yes, and for two reasons.
- Biased players tend to lose more money.
Biased players buy systematically more tickets and — given that the payout rate is 45% in Danish lotto — buying more tickets means losing more money on average. This result suggests that players who are biased in the particular ways studied here may also misperceive the small chance of winning in the first place (the chance of winning the jackpot is about 1 in 8 million in the Danish lotto).
- Biased players tend to win less.
The reason is not that biased players are less likely to win (all numbers are equally likely to win) but that biased players tend to pick the same numbers as other biased players. That is, biased players win smaller amounts given that they happen to win. Lotto has a “pari-mutuel” structure because the prize money per category is fixed and shared among the winners.
Biased players tend to pick the same numbers as other biased players, and such coordinated moves to particular numbers reduce the winnings per player. An extreme example from the Bulgarian 6/42 state lottery illustrates the point. In September 2009, the exact same six numbers were drawn in two consecutive weeks. While no player picked the winning numbers in the first draw, 18 players did in the second draw. These players then had to share the jackpot and lost about 94% of the prize money compared to the case with only one winner.
Conclusion
Using data from the particularly clear-cut case of lotto gambling, this study shows that laypeople tend to draw strong conclusions based on few observations, and that biases are common and systematic when predicting improbable events. In a more general perspective, such biases may induce public opinion and the media to call for dramatic swings in policy in response to highly improbable events. Politicians are then under pressure to yield to popular demands for drastic regulation. However, regulators would be well-advised to be aware of the common tendency to over-infer regularities from rare events and to carefully investigate whether observed data indeed warrants a dramatic swing in policy.
References
Asparouhova, E., Hertzel, M. and Lemmon, M. (2009). Inference from streaks in random outcomes: experimental evidence on beliefs in regime shifting and the law of small numbers. Management Science 55: 1766–1782.
Camerer, C. (1989). Does the basketball market believe in the hot hand? American Economic Review 79: 1257–1261.
Clotfelder, C. and Cook, P. (1993). The “gambler’s fallacy” in lottery play. Management Science 39: 1521–1525.
Croson, R. and Sundali, J. (2005). The gambler’s fallacy and the hot hand: Empirical data from casinos. Journal of Risk and Uncertainty 30: 195–209.
Jørgensen, C.B., Suetens, S. and Tyran, J.-R. (2011). Predicting Lotto Numbers. CEPR Discussion Paper 8314.
Rabin, M. and Vayanos, D. (2010). The gambler’s and hot-hand fallacies: Theory and applications. Review of Economic Studies 77: 730–778.
Tversky, A. and Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletin 76: 105–110.