Over just three decades, the difference in life expectancy across the globe has fallen dramatically (Wilson 2001). In 1970, life expectancy at birth was approaching 54 years among the poorest half of the world, nearly 15 years lower than the life expectancy in richer countries. By 2000, the gap had narrowed to just over 9 years with the poorest expected to live up to 64 and the richest between 73 and 74 years old (Edwards 2008).
For some regions, notably sub-Saharan Africa, the scourge of HIV/AIDS reversed some of this convergence in the 1990s (Moser et al. 2005 and Ram 2006). But even there, strong gains against infant mortality, which strongly influence life expectancy at birth, continued apace. Among developed countries, one observer remarked that convergence in life expectancy was so strong that “the set of the large, established developed countries is behaving increasingly as if it had a single mortality pattern” (White 2002).
But as any actuary or life insurance salesperson might suggest, life expectancy at birth is only part of the story. There are several other characteristics of the distribution of length of life that we might care about. For anyone reading this article, life expectancy at birth is probably out-of-date by the time we reach 6 or 7 years, the age at which we learn to read. By the time we reach 35 –roughly the median age of the population –life expectancy conditional on living to this age is the relevant number. For US females born in 1975, living to age 49 is the relevant age, 45 for males (Bell and Miller 2005). I also cite projections of cohort life expectancies, namely the actual average remaining years based on expected mortality rates in every future year of life, based on extrapolations and educated guesses.1
The second relevant characteristic, especially for insurance purposes, is the probability distribution around the average remaining length of life, which can also be termed inequality2. For females aged 35, the interquartile range between top and bottom is about 16 years. For males, there is more uncertainty or inequality, at 17 years. Other things equal, life insurance should be more expensive for males because their lives are riskier bets.
A final insight relevant for present purposes is that inequality in length of life consists of within- and between-group components. For adult men and women combined in the US, we can conclude that total inequality must reflect inequality between men and women, namely the differences in their remaining life spans from age 35, in addition to reflecting inequality within either group, the 16 or 17 years in interquartile range. Inequality could rise if either component rose, or if they are moving in opposite directions, total inequality could remain unchanged.
None of these characteristics is revealed by life expectancy at birth, which has traditionally been the focus of studies on convergence in length of life. In a new working paper (Edwards 2010), I examine trends in the full distribution of length of life around the world using a new composite data set of high- and low-quality mortality data. My results reveal that trends in inequality in adult length of life since 1970 have been very different to trends in inequality from birth. While the latter has fallen unambiguously because of near-universal gains against infant mortality, the former has remained stagnant in aggregate or even risen. Rising inequality between countries, among rich and poor nations alike, has roughly offset declines in inequality within countries. These patterns appear to contrast with recent dynamics in income or educational inequality and remain mysterious. They are suggestive of rising inequality between countries in other inputs to health, such as technology or healthy behaviours, but such connections remain speculative.
The distribution of length of life
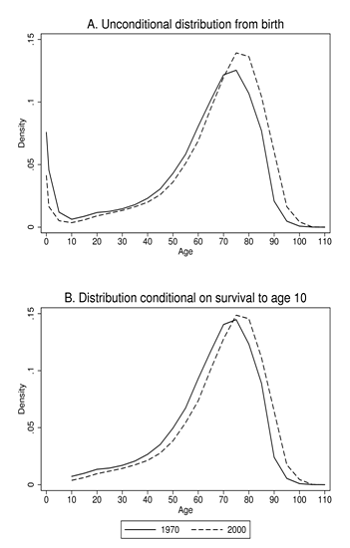
The top panel in Figure 1 depicts the unconditional distributions of global length of life starting from birth in 1970 and 2000 as reported by Edwards. The distributions are hump-shaped around an old-age mode near age 75 with a second, smaller mode at birth and infancy. The latter fell by a large amount after 1970, driving life expectancy at birth much higher.
Figure 1. World distributions of length of life in 1970 and 2000
The bottom panel depicts the same distributions conditional on survival to age 10, an age that is arbitrary but convenient (Edwards and Tuljapurkar 2005). Here, once we have removed the impact of infant mortality, we can see a nearly perfect rightward shift of the adult length of life distribution, resulting in a higher mean adult life expectancy with very little, if any, change in total variance. This dynamic is all but impossible to see or measure in the top panel because trends in infant mortality tend to overwhelm measures of total inequality.
Regional or country-level components
As one might expect based on the heavy incidence of HIV/AIDS in sub-Saharan Africa, the between-region component of inequality is important. Inequality in length of adult life within most regions has fallen as a result of the decline of infectious disease, which tends to cause deaths at all ages (Edwards and Tuljapurkar 2005). But the rising between-region component has been strong enough to offset that effect on total inequality.
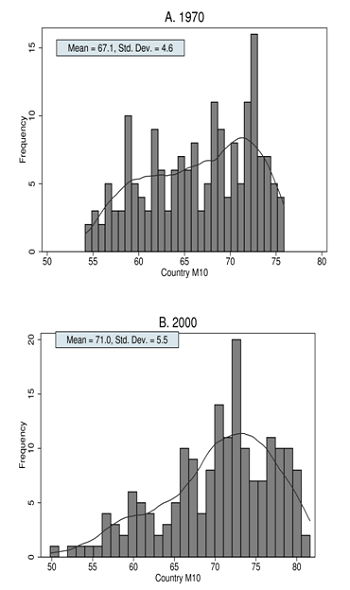
The decomposition analysis I pursue in the paper provides numerical support for these claims, and it is striking how these patterns are robust across multiple subsamples of countries, including advanced nations with high-quality data. The rise in between-country inequality in adult length of life is easiest to depict visually. Histograms of adult length of life in 180 countries are depicted in Figure 2. The top panel shows that the distribution of these country-level averages was much tighter in 1970 than it was in 2000, shown in the bottom panel. The spread or variance in these distributions is the between-country component of total inequality, and it has clearly increased.
Figure 2. Histograms of the mean length of adult life in 1970 and 2000
Implications
The widening in between-country inequality in length of adult life was roughly offset by narrowing within-country inequality, leaving total inequality unchanged, as is visually apparent in the bottom panel of Figure 1. A stable level of total world inequality in adult life span doesn’t sound like a bad thing, especially given that it coincides with declining world inequality in length of life starting from birth due to convergence in infant mortality.
More unambiguously, the finding that the within-country component of inequality in length of adult life has generally declined is welcome. This is not as true for advanced countries where inequality has basically plateaued since the1960s (Edwards and Tuljapurkar 2005).
But widening inequality between countries is not only distressing but also seemingly at odds with what we know about global trends in income and education. Sala-i-Martin (2006) reports the opposite trend in global income inequality, the between-country component of which has been declining. With education, the record is somewhat less clear due to measurement issues, but in any event there do not seem to have been unambiguous increases in between-country inequality that could help account for the trends we see in adult life span.
Other factors such as HIV/AIDS and the socioeconomic upheaval associated with the collapse of communism in the 1990s fare somewhat better in explaining the between-country trends, but a single explanation is elusive. It is tempting to think that healthy knowledge and technologies may have spread more quickly within countries than between them, but this is purely speculative. What may account for the growing divergence in adult mortality between rich and poor countries and also among rich countries themselves is an open question. What seems clear is that mortality convergence has been much stronger at one end of the age spectrum than the other, and that new energies may need to be focused on distributing gains internationally.
References
Bell, Felicitie C and Michael L Miller (2005), “Life Tables for the US Social Security Area, 1900-2100”, Actuarial Study No.120, Office of the Chief Actuary, Social Security Administration.
Edwards, Ryan D (2008), “The Cost of Uncertain Life Span”, Unpublished manuscript, March.
Edwards, Ryan D (2010), “Trends in World Inequality in Life Span Since 1970”, NBER Working Paper 16088.
Edwards, Ryan D and Shripad Tuljapurkar (2005), “Inequality in Life Spans and a New Perspective on Mortality Convergence Across Industrialized Countries”, Population and Development Review, 31(4):645-675.
Goldstein, Joshua R and Ken W Wachter (2006), “Relationships between Period and Cohort Life Expectancy: Gaps and Lags”, Population Studies 60(3):257-269.
Moser, Kath, Vladimir Shkolnikov, and David A Leon (2005), “World mortality 1950–2000: divergence replaces convergence from the late 1980s”, Bulletin of the World Health Organization, 83(3):202-209.
Ram, Rati (2006), “State of the “Life Span Revolution” between 1980 and 2000”, Journal of Development Economics 80(2):518–526.
Sala-i-Martin, Xavier (2006), “The World Distribution of Income: Falling Poverty and ... Convergence, Period”, Quarterly Journal of Economics, 121(2):351-397.
White, Kevin M (2002), “Longevity Advances in High-Income Countries”, Population and Development Review, 28(1):59-76.
Wilson, Chris (2001), “On the Scale of Global Demographic Convergence 1950-2000”, Population and Development Review, 27(1):155-171.
1 There is a difference between period and cohort life expectancies, but the two tend to track one another (Goldstein and Wachter 2006).
2 There is ex ante uncertainty about length of life that surely varies systematically with known characteristics, age and sex being the most obvious. Thus uncertainty and inequality are not the same here. But it is not altogether clear how to decompose the ex post realization of length of life in a population into components that represent uncertainty versus inequality. Instead I refer to the spread in the distribution of length of life based on a life table interchangeably as either uncertainty or inequality.