In the Basel III reform, the level of banks’ minimum capital requirement per risk-weighted assets has been considerably increased. At the same time, the risk weights used to calculate risk-weighted assets have been largely unchanged. However, some observers have criticised the current risk-weighting system, especially the Internal Ratings-Based Approach (IRBA) that the largest banks tend to use.
The IRBA is essentially a credit risk model for a corporate loan portfolio. It assigns a risk weight to each individual loan on the basis of the loan’s contribution to the value at risk, measured in terms of the potential loan losses of the portfolio at a chosen statistical confidence level (the IRBA uses a 99.9% confidence level). Key inputs to the IRBA model are borrower firms’ probabilities of default, and loans’ loss given default ratios.
One concern is that high risk weights for the riskiest corporate borrowers in the IRBA, together with the overall higher capital requirements, may discourage productive business investments. For example, Admati and Hellwig (2013) write that "(t)he current structure of the regulations may actually introduce biases against making (business) loans." Should risk weights therefore be ‘flatter’ with respect to risk than those of the IRBA framework?1
In a recent paper, we consider this question by deriving optimal capital requirements for banks' corporate lending in a model in which firms are credit constrained and may differ in their productivity (Ambrocio and Jokivuolle 2017). We find that the optimal risk weights are indeed flatter than those that are only set to safeguard against bank failures. When risky borrowers are more productive than low-risk borrowers, this flattening effect is amplified. Risk weights should further flatten out if borrower risks are re-evaluated upwards and there is a level increase in capital requirements. Such a situation is one possible interpretation of the move from Basel II to Basel III.
These theoretical results lend support to concerns that the current risk weights, together with the overall higher level of capital requirements, may create a bias against traditional business loans, which would typically obtain a relatively high risk weight in the IRBA system. This further suggests that the IRBA risk-weighting system may not be optimal from the viewpoint of economic growth.2
Model description
Our model is a simple model of banking where financial risks and economic rewards pose a trade-off. Entrepreneurs are borrowers and differ in terms of the default risk and productivity of their sector.3 Importantly, they are collateral constrained and can only borrow up to a fraction of the value of their investment project. This is a key imperfection in credit markets which drives our central result. It is also a notable difference with respect to the portfolio theoretic model underlying the current Basel regulation, which implicitly assumes perfect, frictionless markets. Further, we assume that banks face a non-diversifiable sector-specific risk in their loan portfolios. Hence banks are subject to a failure risk themselves.
Consistent with the view that banks play a special role in facilitating economic activity, bank failures in our model generate social costs which banks do not internalise and hence provide the impetus for capital regulation. Bank equity capital is assumed to be the more costly form of financing for banks than deposits. The tax advantage of debt would be one standard reason for this. Banks are competitive and hence pass on the cost of capital requirements to their borrowers. Loan demand responds accordingly such that capital requirements play a significant role in the allocation of bank credit across sectors.
The mechanism behind the main result works as follows. First, higher capital requirements reduce bank leverage which in turn reduces both the frequency and size of bank failures. Second, higher capital requirements also reduce borrower leverage by raising the cost of borrowing which tightens the collateral constraint. This further reduces the amount of borrowing per unit of borrower net worth. The optimal risk weights trade off these two effects of leverage – the first on bank failure and the second on productive investment.
When comparing IRBA-mimicking risk weights to the optimal risk weights within our model we find the latter to be flatter, even if there are no productivity differences across sectors. The flattening result can be understood as follows. When the risk weight of a sector is raised, the effective borrowing constraint for that sector tightens. As a result, the relative size of the sector diminishes. Not only does this reduce production in the sector, it also reduces the size of the social cost of bank failure arising from that sector. On the other hand, a much larger increase in the risk weight would be needed to induce the same reduction in bank failure probability for a bank lending to a riskier sector relative to a bank lending to a safer sector. In effect, the trade-off between sustaining credit and ensuring banking stability would be tilted too much in favour of banking stability.
Hence, it is better to tolerate a higher probability of failure for banks which lend to high-risk sectors than for banks which lend to low-risk sectors and have a more even distribution of production across sectors. The flattening of risk weights is further amplified if risk and productivity across sectors are positively correlated, and if a higher average level of corporate default risk prompts a higher average level of capital requirements.
Quantitative assessment of the optimal risk weights
To evaluate the quantitative importance of our theoretical results, we match key features of the model with US corporate loan data to assess the relative importance of the misallocation of credit induced by a purely risk-based risk-weighting system. We find that welfare losses from the purely risk-based regulation tend to be small.
More specifically, we use data on internal credit rating grades for US commercial loans taken from the Federal Reserve Board survey of large banking organisations.4 The survey provide information on shares and default probabilities across seven credit grade categories (using the S&P scale) in banks' commercial loan books. The level of the non-diversifiable portfolio risk is calibrated such that for each bank, the bank’s portfolio risk in our model matches with that obtained from the IRBA model.
As the data do not provide a joint distribution of borrower risk and productivity, we consider two cases for the distribution of borrower productivities. First, we assume that all borrowers are equally productive. Second, we assume that riskier borrowers are more productive than safer borrowers and set productivities to seven equally-spaced values (matching the number of rating categories in the data) such that the riskiest borrower is approximately 90% more productive than the safest borrower.5 To match productivities to leverage, we have assumed that the collateral constraint is the same across all borrowers and equal to 30% of borrower net worth.
We consider several values for the cost of bank failures based on estimates from the literature. In particular we consider a conservative value which implies bank failure costs at approximately 15% of output, an intermediate value of 25% of output, and a high value of 33% of output.6
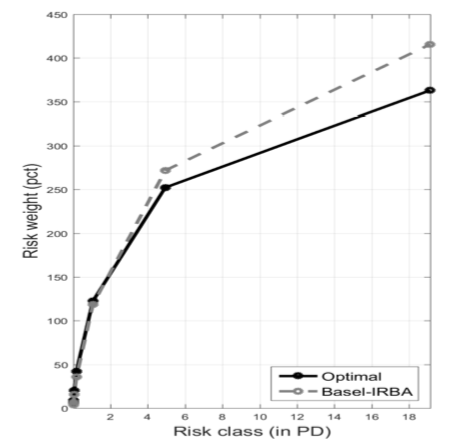
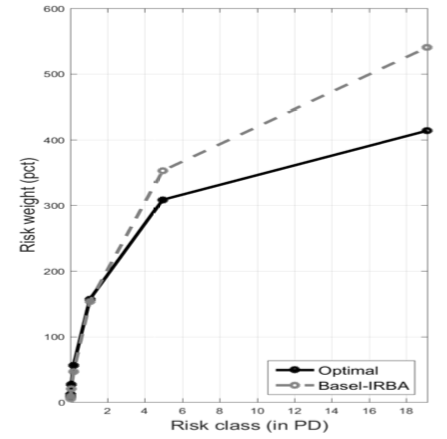
Figure 1 illustrates optimal risk weights against those which represent the IRBA-style risk weights. For the figure, we have assumed that the cost of bank failures is equal to 15% of output. The left plot has productivities constant across borrower sectors. The right plot has the riskier borrowers more productive. The horizontal axis measures borrower sector’s risk in terms of the probability of default and the vertical axis measures the risk weight. It can be seen that the difference between optimal and IRBA-style risk weights is most pronounced for the highest risk borrowers. When risk and productivity are positively correlated (the right-hand plot) the difference is somewhat bigger.
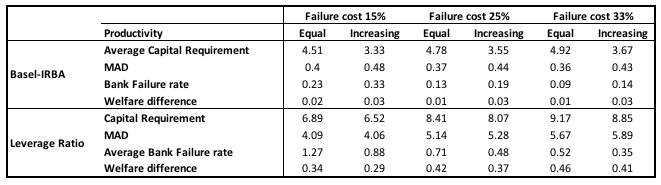
The calibration results are reported in numbers in Table 1. We define welfare cost in terms of percentage difference in expected consumption relative to the optimal. As the table shows, the welfare cost of adopting the purely risk-based capital requirements (‘Basel/IRBA’) appear to be quite modest at up to 0.03%. As Table 1 indicates, this cost is increasing if there is a positive correlation between borrower risk and productivity. The relative difference between the two regulatory schemes becomes smaller the larger the cost of bank failures because then the financial stability aspect of risk weights tends to dominate the credit allocation aspect.
In Table 1 we have also calculated the welfare cost of adopting a regulatory scheme where all corporate loans are charged the same capital requirement, equal to the average of the optimal set (‘leverage ratio’). This scheme, equivalent to a simple leverage ratio requirement on banks, generates marginally higher welfare losses an order of magnitude larger, up to 0.46%.
Figure 1 Optimal vs Basel/IRBA-style risk weights as a function of borrower risk
Notes: Left panel reports risk weights in percent under the scenario of equal productivity. The right panel reports risk weights in percent when the riskier borrowers are more productive. Risk weights are defined as the ratio of the capital requirement in a given sector relative to the average capital requirement for all sectors. Risk categories, in terms of default probabilities (PD), are on the horizontal axes.
As expected, in Table 1 the average level of capital requirements increases in the social cost of bank failures. As a caveat, the model has been primarily designed to study risk weights, not the optimal level of capital requirements, so we do not wish to draw any policy conclusions from the results regarding the level. However, additional analysis with our calibrated model does suggest that from the welfare point of view, it is more important to get the overall level of capital requirements right than fine-tune the risk-weights.
Table 1 Welfare comparison of Basel/IRBA-style capital requirements and a leverage ratio requirement (both with the optimal requirements)
Notes: The first four rows report results when comparing the purely risk-based requirements with the optimal. The first row reports the target bank failure rate under this policy. The second row gives the average capital requirement. The third row reports the mean absolute difference in effective capital requirements in percentage points. The fourth row reports the Welfare loss in percentage terms. The fifth to eighth rows report the same values under a pure leverage ratio requirement. The columns reflect different assumptions with regard to the bank failure costs (from 15 to 33% of output) and productivity differences across sectors. All averages are weighted by sector shares.
Conclusions
There has been much research on the effects and the optimal calibration of the level of capital requirements after the Global Crisis. At the same time, some observers have questioned the current system of risk-weighting based on detailed measurement of risk. Coupled with the level shift of capital requirements in Basel III, are the highest risk weights already discouraging productive investments?
In light of our theoretical model, this is a potential concern. However, based on a quantitative assessment of the model, the answer to the question above is “probably not much”. Hence, the current risk-based capital requirements may not be far off the mark. However, the case for flatter risk weights may be stronger for economies which are more bank-dependent relative to the US, the country from which we have taken the distribution of borrower riskiness in our quantitative assessment. For instance, bank finance is more important for Europe where, in many countries, the heavily bank-dependent small and medium-sized corporate segment is central to the economy. Moreover, our model does not take into account dynamic spillover effects on the productivity of financing innovative but high-risk projects via bank loans. Therefore, we believe that the theoretical issues we have raised may warrant further research.
Finally, it may be argued that the current Basel IRBA risk weights are already lower for the highest risk borrowers than what purely risk-based risk weights would be. This is because of certain smoothing elements agreed on as part of the IRBA rules already in Basel II. Our theoretical results may be seen as providing a possible rationale for these features.
References
Ambrocio, G and E Jokivuolle (2017), “Should bank capital requirements be less risk-sensitive?”, Bank of Finland, Discussion paper10/2017.
Admati, A and M Hellwig (2013), The Banker's New Clothes: What's wrong with banking and what to do about it?, Princeton, NJ: Princeton University Press.
Boyd, J and A Heitz (2016), “The social costs and benefits of too-big-to-fail banks: A ‘bounding’ exercise”, Journal of Banking and Finance 68: 251–265.
Gordy, M B (2000), “A comparative anatomy of credit risk models”, Journal of Banking and Finance 23: 119–149.
Haldane, A (2010), “The $100 billion question”, Bank of England, speech.
Hoggarth, G, R Reis and V Saporta (2002), “Costs of banking system instability: Some empirical evidence”, Journal of Banking and Finance 26: 825–855.
Hsieh, C T and P Klenow (2009), “Misallocation and manufacturing TFP in China and India”, Quarterly Journal of Economics 124(4): 1403–1448.
Syverson, C (2004), “Product substitutability and productivity dispersion”, Review of Economics and Statistics 86(2): 534–550.
Syverson, C (2011), “What determines productivity?”, Journal of Economic Literature 49(2): 326–265.
Endnotes
[1] The IRBA has also been criticised for other reasons, but here we focus only on whether it has unintended implications for credit allocation.
[2] Representatives of the banking industry especially in Europe have also raised concerns that the increased capital requirements (together with the current risk-weighting system) may jeopardise sufficient lending to small and medium-sized enterprises, which are often seen as crucial to European economies. See Christian Clausen, then president of the European Banking Federation, in the Financial Times, 16 November 2014.
[3] To keep things simple in the model, all borrowers in a given sector not only have the same productivity but they also have the same risk characteristics, thus belonging to the same risk weight category. This assumption can be generalised and the results would stay qualitatively the same.
[4] Data on bank portfolios are generally not publicly available. A rare exception are the aggregated portfolio data from Gordy (2000) which we use but which should only be taken as illustrative. For the moment, we have not been able to get European data on banks corporate loans per risk category.
[5] Syverson (2004, 2011) has a ratio of 1.92 for the 90thand 10thpercentile within US manufacturing industries and Hsieh and Klenow (2009) find ratios as high as 5 for China and India.
[6] See Hoggarth et al.(2002) who estimate a 15-20% fall in output in response to banking crises, and Boyd and Heitz (2016) for estimates around 22-27%. On the extreme end of estimates, Haldane (2010) posits a cost of about 1 to 5 times GDP for systemic crises due to their persistent effects.