Policymakers frequently judge the ‘fairness’ or ‘balancedness’ of bilateral trade relationships by looking at trade balances. The most famous producer of such judgements is, of course, the former US president, Donald Trump. Just to mention two examples: On 23 August 2019 he claimed: “Sadly, past Administrations have allowed China to get so far ahead of Fair and Balanced Trade that it has become a great burden to the American Taxpayer”. And five days later, he added that “[t]he vast amounts of money made and stolen by China from the United States, year after year, for decades, will and must STOP”. While no statesmen before Trump has put his or her beliefs so bluntly, similar views have been shared by many for a long time.
Time and again, economists such as Douglas Irwin (2017) have made it more than clear that bilateral trade balances have little to no meaning, at least from a welfare perspective. Bilateral balances are driven by the interaction of aggregate macroeconomic balances with trade costs and specialisation patterns. And they emerge as a consequence of triangular trade – where production and demand patterns are such that a country may have a deficit with one and a surplus with another trade partner while the aggregate position is balanced.
The mystery of the excess trade balances
But, as Feenstra (1998) puts it, “bilateral trade deficits have real consequences on trade policies”. They motivate policymakers to impose protectionist measures or to engage in negotiations. As a result, we need to better understand their origins and their appropriate measurement. But as observed by Paul Krugman in his New York Times column, “[s]omewhat surprisingly, there’s not a lot of economic literature on the causes of bilateral trade imbalances”.
In fact, the only academic paper that Krugman cites is Davis and Weinstein’s (2002) paper in the American Economic Review. They write: “We use the canonical ‘gravity model’ of bilateral trade to form predictions about bilateral trade balances ... Our results paint a dismal picture. The central explanations that economists provide to explain bilateral imbalances fail miserably”. Davis and Weinstein describe their result as the “mystery of excess trade balances” – because actual balances are so much larger than predicted ones. This is a mysterious finding, because it seems at odds with the fact that the gravity model generally provides a good fit to bilateral exports and imports. Recent work by the IMF (e.g. IMF 2019, MacDonald et al. 2020) confirms and reinforces Davis and Weinstein’s finding that the gravity model cannot predict bilateral trade imbalances.
With theory-based gravity modeling, the mystery is solved
In the past few years gravity modelling has undergone a profound transformation. Starting with Anderson and van Wincoop (2003) and Baldwin and Taglioni (2006), researchers have increasingly been able to tie estimation to theory. Head and Mayer (2014) and Yotov et al. (2016) have described the progress made since then. On the theoretical side, it is now well understood that bilateral trade flows – and, hence, bilateral trade balances – are not only influenced by bilateral trade costs but by the trade partners’ average trade costs with all countries in the world – the so-called ‘multilateral resistances’. On the empirical side, it has turned out to be necessary to properly account for those resistances. Further, various authors have shown that the gravity model is best estimated using not only international but also intranational trade flows, that the ‘Poisson estimator’ is a natural pendant to the theoretical gravity model, and that care should be devoted to properly measuring both the supply side (using output) and demand side (using expenditure).
In Felbermayr and Yotov (2021), we revisit Davis and Weinstein’s mystery. We find that gravity predicts bilateral balances very well once theory-consistent estimation is applied, leaving only very little space for unfair (i.e. asymmetric) bilateral trade costs. But let us start by revisiting the initial finding.
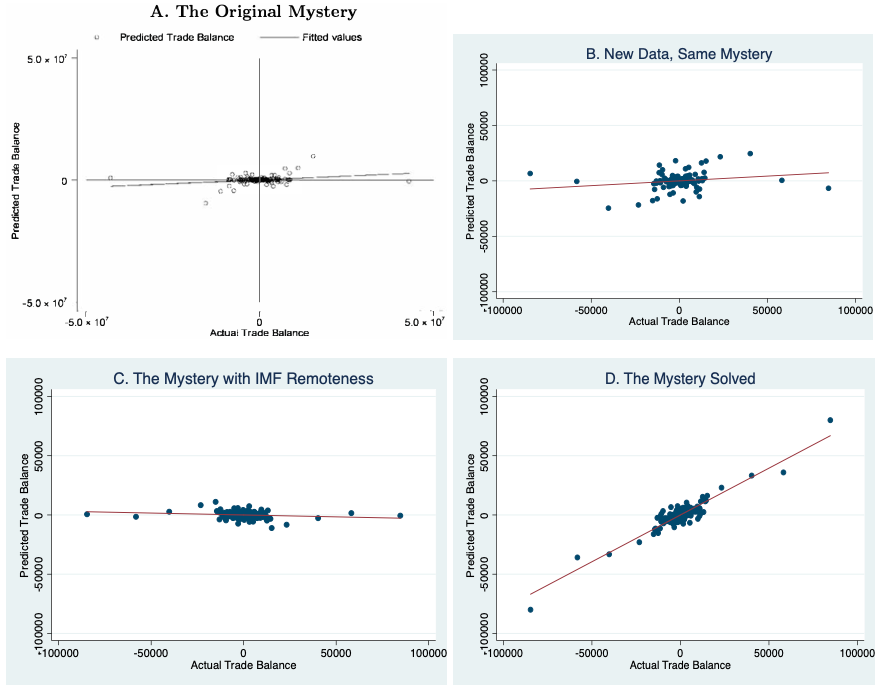
Davis and Weinstein used a standard (as of 2002) gravity model, estimated it on bilateral export flows from the year 2000, predicted those flows, and then used the predictions to calculate predicted bilateral balances. Panel A of Figure 1 reproduces this original picture, which correlates actual and predicted balances. The gravity model predicts only 7% of the variance in actual balances and gets the sign right in only 54% of all cases – not significantly better than if one were to toss a coin. We show that, using an alternative database for the same year, this dismal picture does not change. Panel B shows the outcome. Panel C confirms the finding of IMF economists MacDonald et al. (2020), who chose a different ‘atheoretical’ way of proxying for the overall remoteness of countries.
But if one follows the four suggestions of modern gravity modeling stated above, the performance is much improved. Panel D shows that predicted and actual trade balances lie very close to the 45° line. Indeed, 86% of variance can be successfully explained, and the sign of 72% of all bilateral balances is correctly predicted. As with Davis and Weinstein, our model does not contain asymmetric measures of bilateral trade costs. It also does not contain any fixed effects, but multilateral resistances are constructed consistent with theory. An upshoot of this is that we do not need large asymmetric trade costs to explain bilateral balances. In other words, the potential role for unfair policies is rather small.
So, in its modern incarnation, the gravity model is quite successful in predicting bilateral trade balances. In our paper, we show that this success is not specific to a particular year. It also holds at the sectoral level. For example, in the highly important machinery sector, the explanatory power of the model is above 90%. Estimating and predicting sector-by-sector, we find a fit of 88% for manufacturing trade. It should also be noted that the ‘big’ trade links are all correctly signed; wrong signs are limited to small trade links.
Figure 1 Gravity and bilateral trade balances: From failure to success
Note: Panel A of this figure is Figure 1 from Davis and Weinstein (2002), which visualizes the mystery of excess trade balances by showing that predicted balances are an order of magnitude smaller as compared to actual balances. Panel B reproduces the results from D&W with the data from Baier et al. (2016), and confirms the mystery of excess trade balances. To obtain the results in Panel C, we use the same data as those in Panel B, but we follow the approach of the World Economic Outlook (2019) and MacDonald et al. (2020) to construct the proxies for the multilateral resistances. Finally, Panel D is obtained with the same data as in the previous two panels but after introducing the adjustments to the original specification of D&W, which we describe in the text.
What solved the mystery? The role of the structural multilateral resistances
Our results beg the question: Why is the modern gravity model successful? Or, in other words, why do the models of Davis and Weinstein (2002) or MacDonald et al. (2020) fail to predict bilateral balances while ours is so much more successful? Figure 2 provides the answer.
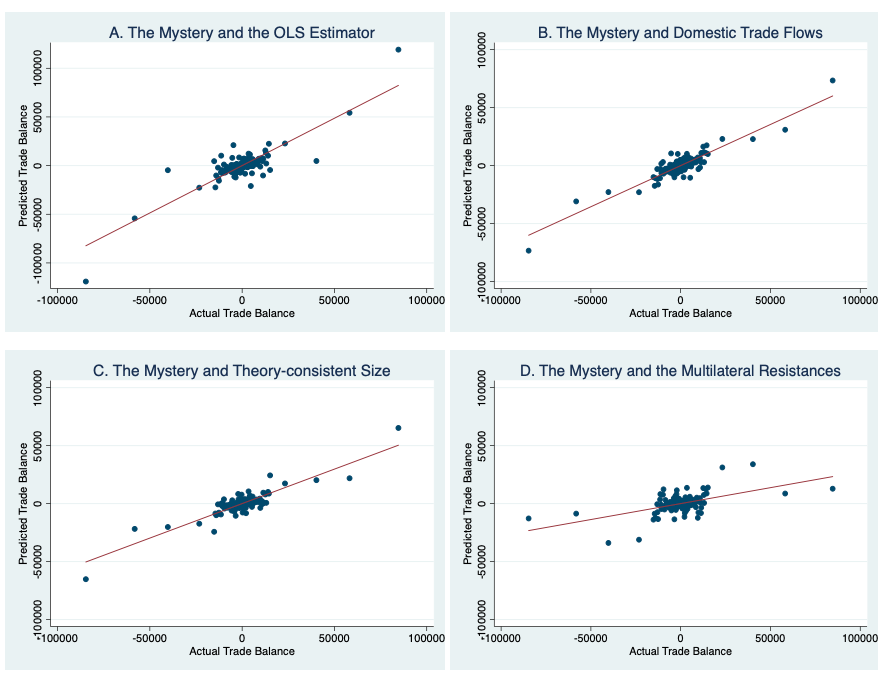
We change one of our main estimation or modeling choices at a time, keeping all the others unchanged, and check whether the model still fits the data. Panel A is constructed based on a gravity model that uses Ordinary Least Squares (OLS) instead of poisson pseudo maximum likelihood (PPML). The goodness of fit (or R2) falls to 0.73. In our baseline it is 0.86. But the estimated regression coefficient is almost identical to unity. We conclude that the choice of estimation technique is not key. Next, instead of including domestic trade, we estimate the model on international trade flows only. Panel B shows that this makes little difference. The R2 of the regression line shown in the diagram is equal to 0.82, only slightly less than in our baseline model. Panel C reverts to the size controls used Davis and Weinstein (2002) instead of the theoretically motivated ones in our baseline. This has a relatively strong effect on the coefficient of the regression line which falls to 0.59, with the R2 remaining at 0.78.
Figure 2 Who solved the mystery? Multilateral resistances
Note: This figure sheds light on the relative importance of the alternative improvements that we implement to resolve the mystery of the trade balances. Panel A implements all improvements except the PPML estimator. Instead, the results in this panel are obtained with the OLS estimator. Panel B implements all improvements except the addition of domestic trade flows/costs. Panel C implements all improvements except for the theoretically motivated size controls. Finally, the results in Panel D are obtained with all other adjustments but with the a-theoretical remoteness indexes instead of the structural multilateral resistances.
Finally, Panel D keeps all improvements relative to Davis and Weinstein’s model in place except for the multilateral resistances which are replaced by a-theoretical ‘remoteness’ indices. This lowers the estimated coefficient of the regression line in the diagram to 0.28 and the R2 value to 0.29. This is better than the performance of the original specification, but a far shot from our baseline model. In the paper, we show that the performance of the model does not improve when the remoteness indexes are constructed following the methods from the World Economic Outlook (IMF 2019). We also demonstrate the importance of the structural multilateral resistances by implementing an iterative procedure to construct them. We do this by following Anderson and van Wincoop (2003) and by showing that the fit of the model improves with each iteration, bringing us closer to the true theoretical multilateral resistance terms. Hence, we conclude that the model fits the data when multilateral resistance terms are constructed according to theory. As a result, our findings reinforce the message from Baldwin and Taglioni (2006) that not controlling for the multilateral resistances is a ‘gold medal mistake’, and the argument from Head and Mayer (2014) that proxying for the structural multilateral resistances with a-theoretical remoteness indices may not be enough.
What it all means
It is straightforward to see that the standard one-sector gravity model cannot generate bilateral trade imbalances if trade is balanced at the aggregate level and direct bilateral trade costs are symmetric. But as we have shown, even if expenditure and revenue differ at the macro-level, the model does not explain the data well. What one needs is proper modeling of multilateral resistance terms. These terms reflect the average inward and outward trade costs that the exporter and the importer face relative to the while world. Their proper calculation makes use of aggregate expenditure and revenues around the world as well as of bilateral trade costs of all countries with each other. These are (with the exception of tariffs) essentially unobservable and need to be estimated with the help of the general equilibrium trade model that gives rise to gravity. Together with bilateral trade costs, the multilateral resistances account for the difference between friction-free bilateral trade and bilateral trade in the presence of trade costs.
This means that the best way to interpret our results is to understand that total bilateral trade costs are made up by the direct bilateral trade costs and the multilateral resistances. Because inward and outward resistances generally differ (reflecting aggregate outcomes and bilateral trade costs of each country’s trade partners), even if bilateral trade costs are symmetric, total trade costs are not. Crucially, this is not the case with the a-theoretical remoteness measures as used by Davis and Weinstein (2002) or MacDonald (2020). So, the theory-grounded gravity model can go a far way in matching observed bilateral balances even in the absence of direct asymmetries in trade costs.
Limited leeway for unfair trade policies
Our results suggest that the observed bilateral trade balances can be rationalised by aggregate outcomes (driven, among other things, by countries’ fiscal and monetary policies) and by symmetric bilateral trade costs (both explicit trade policy such as tariffs and unobservable trade costs related to non-tariff trade costs or other (e.g., cultural) impediments to trade). The scope for ‘unfair’ (i.e. non-reciprocal) bilateral trade policy is, therefore, small. On average, at most 12% of variance in bilateral positions can be attributed to asymmetric trade barriers. As a result, it remains true that if a country wishes to reduce an overall trade deficit, it needs to turn towards its fiscal or monetary policy. An obsession with unfair or unbalanced bilateral trade will not take it very far.
References
Anderson, J and E van Wincoop (2003), “Gravity with Gravitas: A Solution to the Border Puzzle”, American Economic Review 93 (1): 170–192.
Arkolakis, C, A Costinot and A Rodriguez-Clare (2012), “New Trade Models, Same Old Gains?”, American Economic Review 102 (1): 94–130.
Baldwin, R E and D Taglioni (2006), “Gravity for Dummies and Dummies for Gravity Equations”, NBER Working Paper 12516.
Davis, D and D Weinstein (2002), “The Mystery of the Excess Trade (Balances)”, American Economic Review 92 (2): 170–174.
Feenstra, R, W Hai, W T Woo and S Yao (1998), “The U.S.-China Bilateral Trade Balance: Its Size and Determinants”, NBER Working Paper 6598.
Felbermayr, G and Y Yotov (2021), “From Theory to Policy with Gravitas: A Solution to the Mystery of the Excess Trade Balances”, CESifo Working Paper 7825.
Head, K and T Mayer (2014), “Gravity Equations: Workhorse, Toolkit, and Cookbook”, in Gopinath, G, E Helpman and K S Rogoff (eds), Handbook of International Economics, Volume 4, Oxford, UK: Elsevier Ltd
IMF (2019), “World Economic Outlook, Growth Slowdown, Precarious Recovery”, International Monetary Fund.
Irwin, D (2017), Clashing over Commerce: A History of U.S. Trade Policy, Chicago, IL: University of Chicago Press.
MacDonald, M, R Piazza, J Eugster and F Jaumotte (2020), “Are Bilateral Trade Balances Irrelevant?,” IMF Working Papers 2020/210, International Monetary Fund.
Yotov, Y, R Piermartini, J-A Monteiro and M Larch (2016), An Advanced Guide to Trade Policy Analysis: The Structural Gravity Model, Geneva: UNCTAD and WTO.