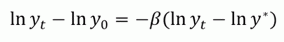The historical evidence on population growth, food consumption, wages, and taxes suggests that the average citizen in Napoleonic Europe was little better off than the average person living in the Roman Empire. The contrast between the lack of growth before the industrial revolution and great divergence in growth rates afterwards is a quintessential puzzle in economics.
Modern growth theory such as Galor (2011) and historical accounts such as Clark (2007) attribute pre-industrial stagnation to the Malthusian trap – an 'iron law of wages' driven by changes in population.
The econometric evidence for pre-industrial Europe, however, does not offer much support to this idea. While researchers often find a significant relationship between incomes and population growth, it also consistently finds that the elasticities of population growth with respect to wages were small – too small to prevent wage growth in the face of changes in productivity and technology.
A Malthusian model
We use a new empirical strategy to evaluate whether the Malthusian trap was responsible for wage stagnation (Madsen et al. 2019). To borrow a phrase from a classic paper by Mankiw et al. (1992), we “take Thomas Malthus seriously" by deriving a parsimonious and familiar empirical model from a fully-specified Malthusian model based on household fertility choices.
In the steady state, constant technological progress leads to constant population growth, but with no wage or income growth. The steady state of the model generates the iron law of wages.1
Figure 1 shows the equilibrium. The upward-sloping curve shows the typical Malthusian relationship between the rate of population growth, 1 + n, measured on the vertical axis, and per capita income, y, on the horizontal axis. The vertical axis also measures productivity growth, due for example to technological change or land cultivation. Productivity grows exogenously at rate 1 + g.
Figure 1 Steady state in a Malthusian model of household fertility choice
Source: Madsen et al. (2019)
For any value of y that is greater than y*, the population growth rate will exceed the growth rate of productivity since n is greater than g, and so per capita income will decline. Likewise, for any y less than y*, productivity growth is greater than population growth, and per capita income will rise. Hence per capita income is constant at the point where y is equal to y*. At this equilibrium the rate of population growth equals the exogenous productivity growth rate and per capita incomes and wages are constant.
Linearising around this steady-state yields a familiar model of convergence for per capita income or wages, of the type that has been widely used in growth empirics based on the neoclassical growth model.2 Per capita income growth can thus be modelled as linear function of a lagged dependant variable and other variables that control for differences in the steady-state per capita income levels.
The empirical model looks superficially similar to the empirical version of the Solow-Swan model in Mankiw et al. (1992), and can be empirically implemented in the same way, but its interpretation is very different. This is because convergence is driven by changes in population growth rates, and not in capital accumulation. Specifically, the convergence coefficient depends on the curvature of the upward-sloping population growth curve in Figure 1. Convergence will be faster when population growth is steeper, and so is more sensitive to changes in income.
The model can be tested in the usual way, by adding an error and using control variables to allow for changes in the steady-state per capita income, y*. This approach avoids concerns about simultaneity because both population and wage are endogenous. And because population is endogenous, we can derive a similar linearised convergence for population.
Applying wage, income and population data
We constructed a per capita income and population data set for 17 European countries between 900CE and 1870CE to test the model. It provides more regular time series observations than the standard sources, and allows us to test the generality of the Malthusian mechanism by including many countries.
Across different time and country subsamples, we consistently find convergence rates between 2% and 3% per year. These are an order of magnitude larger than previous results.
As an example, our estimates imply half-lives of population and incomes between 11 and 12 years. Previous estimates found half-lives of several centuries, if not thousands of years. With such long half-lives the model predicts near unit root behaviour, suggesting the Malthusian era would have been characterised by a stochastic trend in wages. Faster convergence allows us to reconcile Malthusian theory with the stylised fact that wages were constant throughout history before the industrial revolution. Interestingly, our convergence rates are also similar to estimates of convergence rates for the modern growth era, as characterised by the ‘law of convergence’ in Barro (2015).
Overcoming Malthusian forces
Our results provide the first econometric evidence that Malthusian forces were sufficiently strong and widespread to explain the economic stagnation from the dark ages to the industrial revolution. This supports the claim of unified growth theories that claim that overcoming Malthusian forces was critical for the transition to modern growth (Galor 2011).
This result is also important because Malthusian population theory informs fertility policies in developing countries – specifically, whether technological progress can outrun population increases in the absence of population policy.
References
Barro, R J (2015), "Convergence and modernisation", The Economic Journal 125(585): 911-942.
Baumol, W J (1983), "Marx and the iron law of wages", American Economic Review 73(2): 303–308.
Clark, G (2007), A farewell to Alms, Princeton University Press.
Galor, O (2011), Unified growth theory, Princeton University Press.
Madsen, J B, P E Robertson, and L Ye (2019), “Malthus was right: Explaining a millennium of stagnation”, European Economic Review 118: 51-68.
Mankiw, N G, D Romer, and D N Weil (1992), “A contribution to the empirics of economic growth”, The Quarterly Journal of Economics, 107(2): 407-437.
Endnotes
[1] Marx popularised the description "iron law" in the context of Malthus, though Marx himself rejected the idea since he argued workers could raise wages by influencing the distribution of income (Baumol 1983).
[2] That is,
where y is per capita income, y* is steady state per capita income, and beta is the convergence rate.