For policymakers and healthcare providers, prediction of the evolution of an epidemic is extremely important (Manski 2020, Castle et al. 2020). Timely and reliable projections are required to assist health authorities, and the community in general, in coping with an infection surge and to inform public health interventions such as enforcing (or facilitating) local or national lockdowns (Heap et al. 2020). Weekly forecasts of the evolution of the COVID-19 pandemic generated by various independent institutions and research teams have been collected by the Centers for Disease Control and Prevention (CDC) in the US.1 These forecasts are intended to inform the decision-making process for public health interventions by predicting the impact of the COVID-19 pandemic for up to four weeks. However, this wealth of forecasts also poses a problem: how to act when confronted with heterogeneous forecasts and, in particular, how to select the most reliable projections.
Forecasting teams, methods, and assumptions
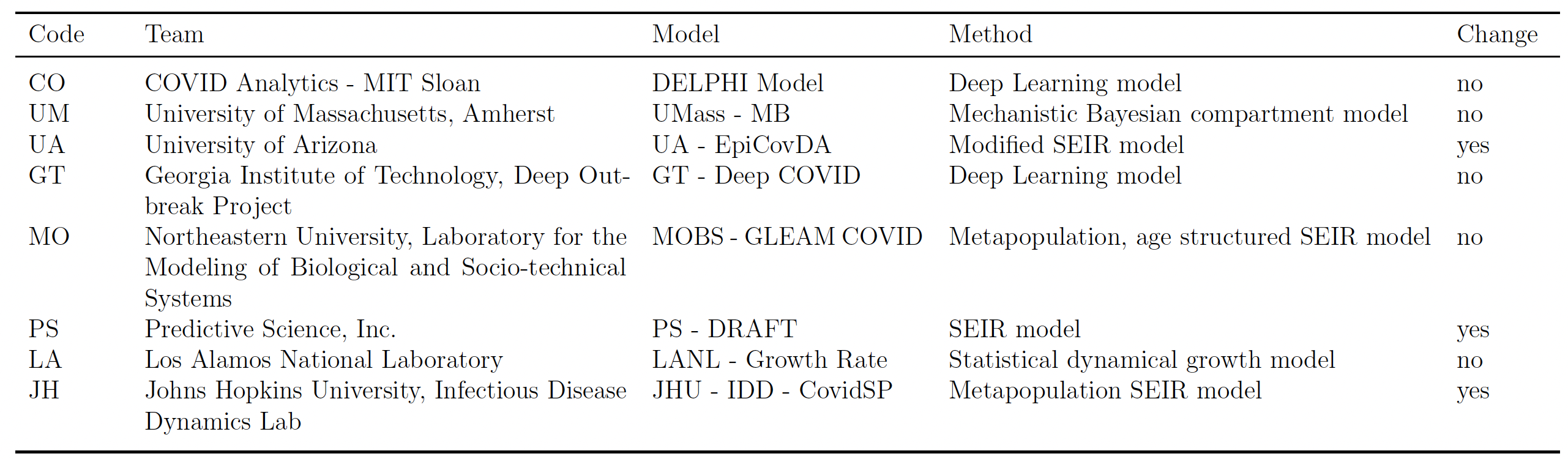
The forecasting teams include data scientists, epidemiologists, and statisticians. They use different methodologies and approaches (e.g. the susceptible-exposed-infectious-recovered (SEIR), Bayesian, and deep learning models) and combine a range of data sources and assumptions concerning the impact of non-pharmaceutical interventions on the spread of the epidemic (such as social distancing and the use of face coverings). In Table 1, we report the eight teams that continuously submitted their predictions since the start of the pandemic, for the period 20 June 2020 to 20 March 2021.
Table 1 Forecasting teams, methods, and assumptions
Notes: The column code describes the code given in the empirical analysis to each team. A forecasting team is included if it submitted its predictions for all the weeks in our sample. The table reports for each forecasting team the modelling methodology and whether the model considers a change in the assumptions about policy interventions. In the fourth column, “yes“ means that the modelling team makes assumptions about how levels of social distancing will change in the future, while “no” means that it is assumed that the existing measures will continue through the projected 4-week time period.
We consider the forecasting teams in Table 1 as individual forecasters, and we also combine them in a pooled forecast average (with equal weights) that we call ‘core ensemble’. Finally, we also consider the ensemble forecast produced by the CDC, which is obtained by combining a wider group of forecasting teams.2
Our forecasting evaluation test
The standard test usually implemented to compare equal predictive accuracy is the Diebold and Mariano (1995) test (henceforth, DM test). The DM test is the most suitable test for comparing competing forecasts from a model-free perspective, as in this application. It works very well when a long history of forecasts is available. However, implementing the DM test is challenging when only a few out-of-sample observations are available. Since in this case, large size distortions make the test unreliable. To overcome this small-sample problem, we apply fixed-smoothing asymptotics as proposed by Coroneo and Iacone (2020). This approach enables accurate implementation of the DM test, even when the available number of out-of-sample observations is small.
Empirical analysis
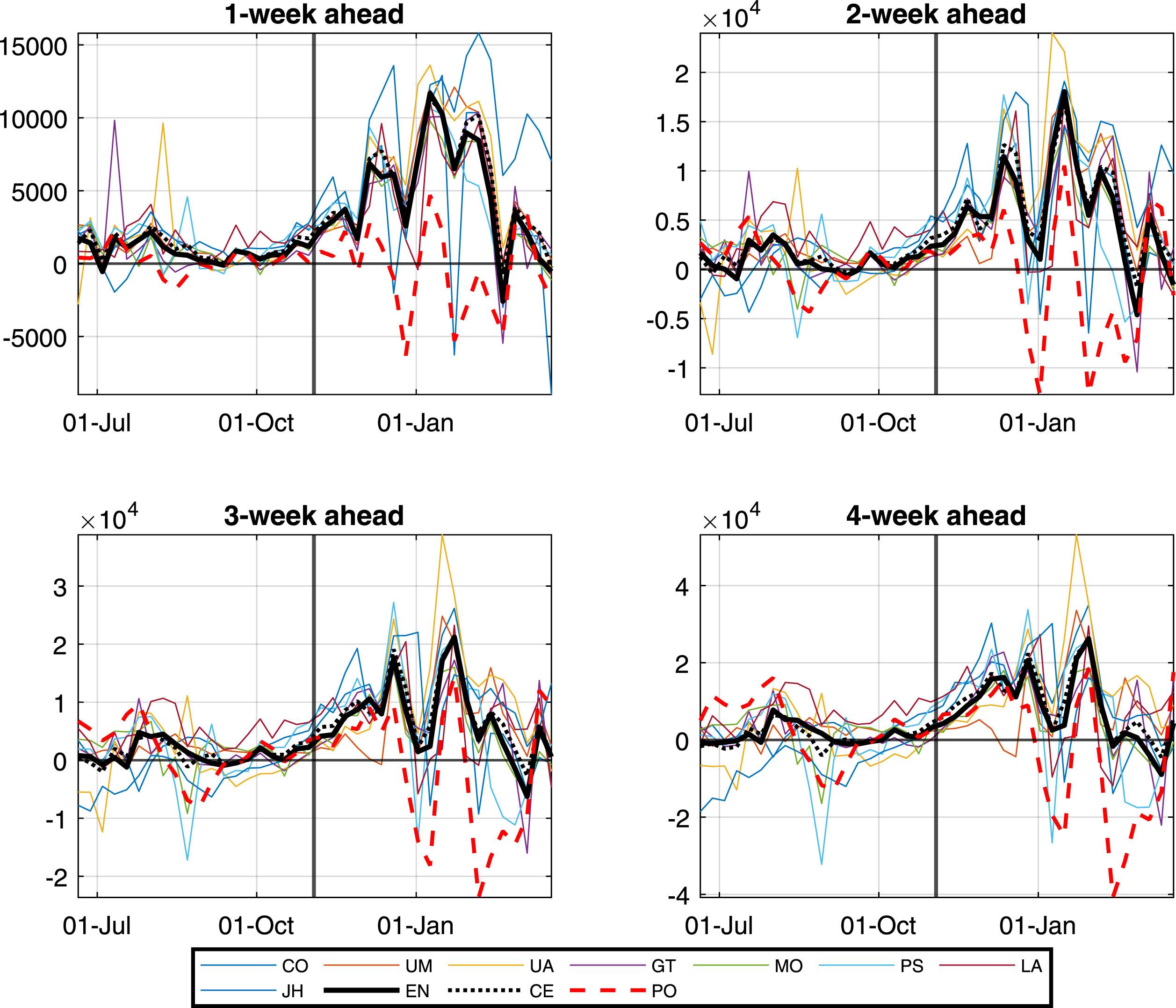
We assess forecasts for the total number of COVID-19 deaths at the national level for the US by the eight forecasting teams that submitted their forecasts to the CDC without interruption from 20 June 2020 to 20 March 2021. Even though the evaluation period only includes 40 observations, we find an increase in the volatility of forecasting errors in November 2020. As a result, we conduct our forecast evaluation separately on two sub-samples: from 20 June 2020 to 31 October 2020, and from 7 November 2020 to 20 March 2021. Figure 1 illustrates each model's prediction errors (computed as the difference between the realisation and the point forecast). It shows that most forecast teams have underestimated the number systematically, in particular in the second part of the sample. Of course, this is relevant if the costs of over-predicting and under-predicting differ.
Figure 1 Forecast errors
Note: Forecast errors at forecasting horizons from 1 to 4 weeks. Weekly observations from June 20, 2020 to March 20, 2021. The vertical line indicates November 3, 2020 and delimits the two sub-samples. The names of the forecasting teams are as in Table 1; EN denotes the ensemble forecast, CE denotes the core ensemble, and PO the polynomial benchmark. Forecast errors are defined as the realised value minus the forecast.
We compare the predictive accuracy of the forecasts provided by the eight teams in Table 1 and the two ensemble forecasts to those of a simple benchmark model constructed by fitting a second-order polynomial using a rolling window of the previous five available observations (Coroneo et al. 2021).
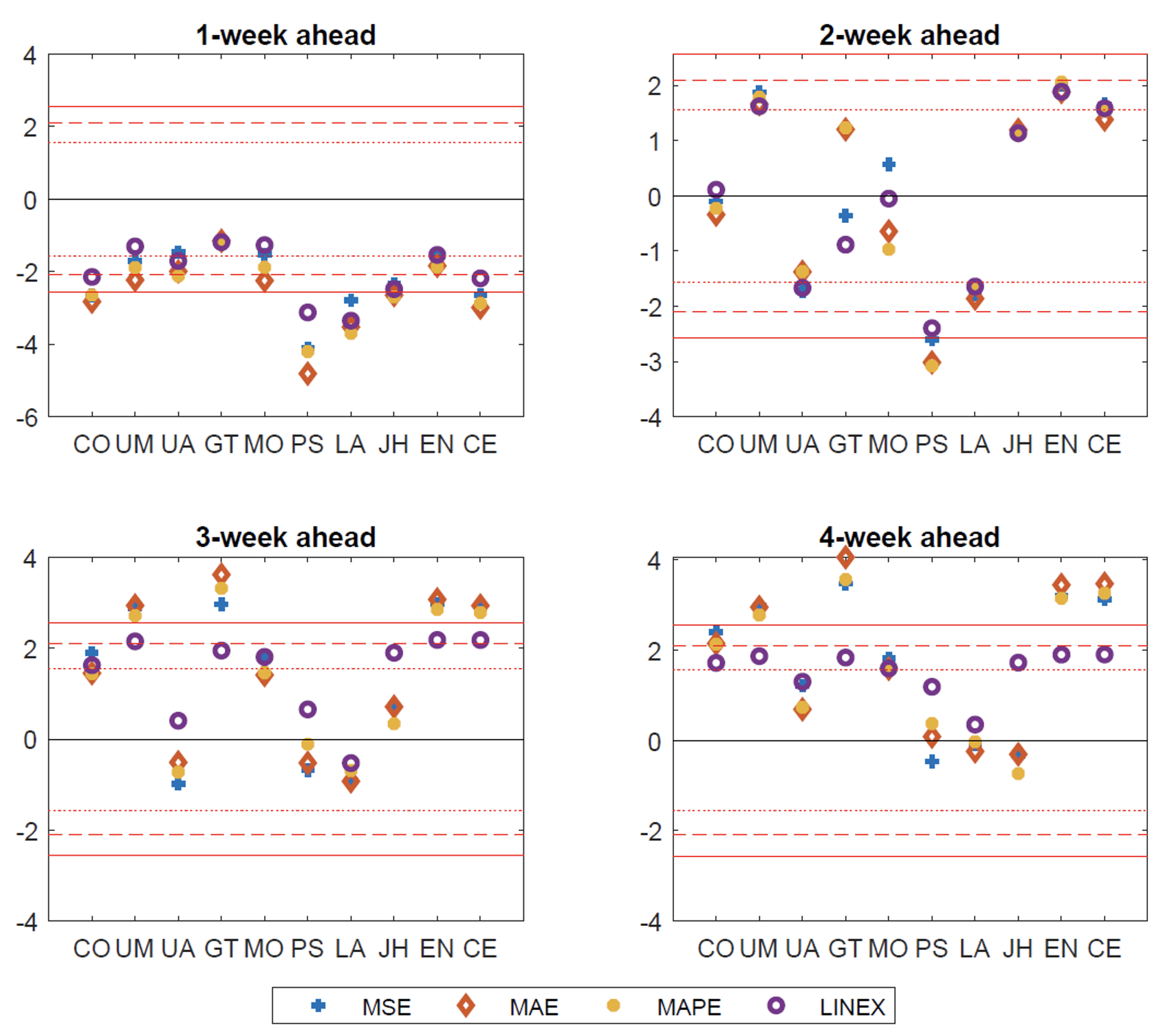
Results for the test of equal predictive accuracy are reported in Figures 2 and 3. We apply the Diebold and Mariano test (1995) using fixed-b asymptotics as in Coroneo and Iacone (2020), and consider different loss functions: mean square errors (MSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and linear exponential (linex) loss function. A positive value of the test statistic indicates better performance of the forecasting team with respect to the benchmark polynomial model.
Figure 2 Forecast evaluation with weighted covariance estimator: The first evaluation sub-sample
Note: This figure reports the test statistic for the test of equal predictive accuracy using the weighted covariance estimator (WCE) of the long-run variance and fixed-asymptotics. The benchmark is a second degree polynomial model fitted on a rolling window of 5 observations. A positive value of the test statistic indicates lower loss for the forecaster, i.e. better performance of the forecaster relative to the polynomial model. Different loss functions are reported with different markers: plus refers to a quadratic loss function, diamond to the absolute loss function, filled circle to the absolute percentage loss function and empty circle to the asymmetric loss function. The dotted, dashed and continuous red horizontal lines denote respectively the 20%, 10% and 5% significance levels. The forecast horizons are 1, 2, 3 and 4 weeks ahead. The evaluation sample is June 20, 2020 to October 31, 2020.
Figure 3 Forecast evaluation with weighted covariance estimator: The second evaluation sub-sample
Note: This figure reports the test statistic for the test of equal predictive accuracy using the weighted covariance estimator (WCE) of the long-run variance and fixed-asymptotics. The benchmark is a second degree polynomial model fitted on a rolling window of 5 observations. A positive value of the test statistic indicates lower loss for the forecaster, i.e. better performance of the forecaster relative to the polynomial model. Different loss functions are reported with different markers: plus refers to a quadratic loss function, diamond to the absolute loss function, filled circle to the absolute percentage loss function and empty circle to the asymmetric loss function. The dotted, dashed and continuous red horizontal lines denote respectively the 20%, 10% and 5% significance levels. The forecast horizons are 1, 2, 3 and 4 weeks ahead. The evaluation sample is November 7, 2020 to March 20, 2021.
Our main findings are as follows. First, although the simple polynomial benchmark outperforms the forecasters at the short horizon (one week ahead), the forecasters become more competitive at longer horizons (three to four weeks ahead). They sometimes outperform the benchmark and, thus, confirm the importance of epidemic modelling. This suggests that forecasts can help inform future policy decisions successfully. Second, the ensemble forecasts are among the best performing forecasts, especially during the first sub-sample. The reliability of the ensemble forecasts underlines the virtues of model averaging when uncertainty prevails and supports the view in Manski (2020) that data and modelling uncertainties limit our ability to predict the impact of alternative policies using a tight set of models. Overall, our findings hold for all the loss functions considered and caution health authorities not to rely on a single forecasting team (or a small set) to predict the evolution of the pandemic. A better strategy appears to be to collect as many forecasts as possible and to use an ensemble forecast.
Conclusions
Our empirical analysis indicates that forecasts of the COVID-19 epidemic are valuable but need to be used with caution. Decision-makers should not rely on a single forecasting team (or a small set) to predict the evolution of the pandemic, but should hold a large and diverse portfolio of forecasts.
References
Castle, J, J A Doornik and D Hendry (2020), “Short-term forecasting of the coronavirus pandemic”, VoxEU.org, 24 April.
Coroneo, L and F Iacone (2020), “Comparing predictive accuracy in small samples using fixed-smoothing asymptotics”, Journal of Applied Econometrics 35(4): 391– 409.
Coroneo, L, F Iacone, A Paccagnini and P S Monteiro (2021), “Testing the predictive accuracy of COVID-19 forecasts”, International Journal of Forecasting, forthcoming.
Diebold, F X, and R S Mariano (1995), “Comparing predictive accuracy”, Journal of Business & Economic Statistics 20(1): 134-144.
Heap, S P H, C Koop, K Matakos, A Unan, and N Weber (2020), “Valuating health vs wealth: The effect of information and how this matters for COVID-19 policymaking”, VoxEU.org, 6 June.
Manski, C F (2020), “Adaptive diversification of COVID-19 policy”, VoxEU.org, 12 June.
Manski, C F (2020), “Forming covid-19 policy under uncertainty”, Journal of Benefit-Cost Analysis 11(3): 341-356.
Endnotes
1 https://www.cdc.gov/coronavirus/2019-ncov/science/forecasting/forecasting-us.html
2 As it also includes teams that did not submit their forecasts every week.