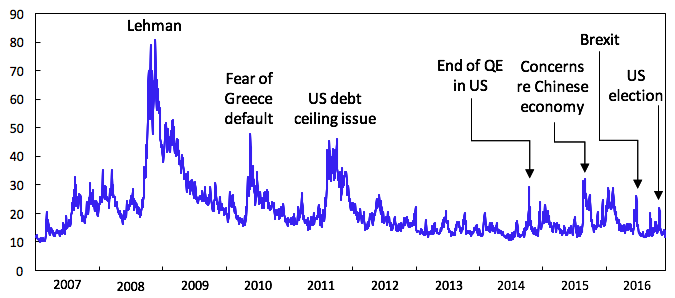
The US election, the Brexit referendum, Lehman’s bankruptcy, and debate about debt repayments in Greece – all these events were surprising and created uncertainty about future outcomes (see Figure 1). These types of shocks fall into a broad class that economists have recently labelled uncertainty shocks. As well as being a powerful restraint on growth in the modern economy (see Bloom 2009 and Van Nieuwerburgh and Veldkamp 2006), uncertainty has been used as a driving force in models of economic fluctuations, to explain asset prices, and to trigger financial crises.
Figure 1. VIX, 2007-2016
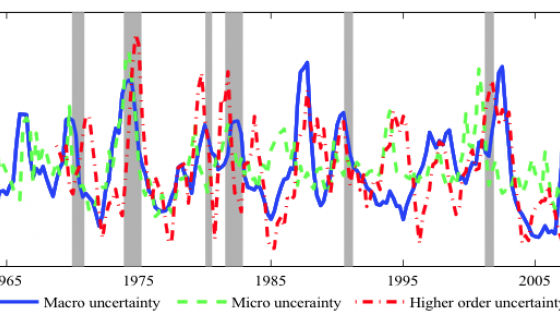
While uncertainty shocks are often discussed as if they are a single phenomenon, in the process of incorporating them into theories economists have looked at uncertainty about at least three distinct things:
- Often it is uncertainty about an aggregate variable, such as total factor productivity (TFP) or GDP.1 We refer to this as macro uncertainty.
- In other cases, the focus is on the uncertainty that firms have about their individual outcomes.2 We call this micro uncertainty.
- The third type is uncertainty that people have about the beliefs of others, which we call higher-order uncertainty.3
These three types of uncertainty are not only conceptually distinct, but are usually modelled independently. Macro uncertainty shocks are linked to changes in the variance of an aggregate shock, micro uncertainty shocks to changes in the variance of a firm-specific shock, and high order uncertainty arises from private signal noise. Since these three types of uncertainty come from three different types of shocks which could be independent of each other, we wouldn’t expect them to covary, and yet, they do. Exploring why these uncertainty measures covary helps us understand where all economic uncertainty comes from.
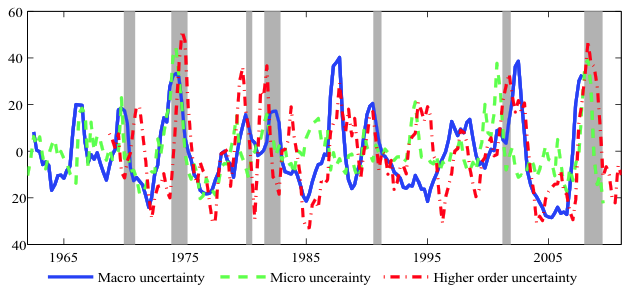
Figure 2 shows the percentage deviations from trend of the three types of uncertainty in recent decades.4 We could generate this comovement by assuming that the three shocks are correlated, but this isn’t the same as understanding why there is comovement. Since all three series are countercyclical, one possible explanation for their correlation is that the variables have no relationship to each other except that they covary negatively with economic output. However, when we estimate their relationship linearly, controlling for GDP growth, the three series have statistically significant relationships with each other, above and beyond what GDP growth can explain. So there must be another explanation.
Figure 2. Percentage deviation from trend of macro, micro and higher-order uncertainty
Kozeniauskas et al. (2016) argue that all three types of uncertainty are related because all three are tied to disaster risk. To show this, we build a unified framework for understanding how macro uncertainty shocks can be passed on to micro and high-order uncertainty. The model has three key ingredients: 1) TFP growth captures the risk of disasters by being negatively skewed; 2) each person in the economy receives some private information each period; and 3) people don’t know the parameter values of the economic model — they estimate them each period using observed data. In this setting, we introduce an exogenous source of macro uncertainty shocks, in the form of a heteroskedastic TFP process. Importantly we don’t assume that these shocks are countercyclical. It remains for the model to generate uncertainty that rises in recessions, and the concurrent rises in micro and higher order uncertainty. The TFP process and each of the model’s features are carefully disciplined by data.
To determine agents’ beliefs, we assume that agents are in the same position as an econometrician would be in: they observe new data each period and can re-estimate their model. Although perfectly consistent with rationality, this approach contrasts with rational expectations. Rational expectations typically mean that the perceived distribution of economic outcomes and the true distribution coincide. While agents in our model are fully rational, they do not satisfy this definition of rational expectations because they do not know the true distribution of outcomes. While it is obvious that real people do not know the true probabilities of all possible shocks, implementing this idea poses problems for theorists. If agents do not know the true distribution, what do they know? How do we discipline the choice of beliefs? If we can allow them to believe anything, we can explain almost any outcomes. How do we then write theories that are falsifiable? Our solution to this quandary is to use econometrics to discipline beliefs. Our agents are simply econometricians using observed macro outcomes and standard econometric tools to estimate parameters of the true distribution. They are no more omniscient and no less rational than any econometrician in the economics profession.
Disaster risk is the key component of the model for generating large uncertainty shocks that are countercyclical, as we see in the data. The reason is that disasters arise infrequently, making disaster forecasts error-prone and the scope for disagreement large. When the economy enters a bad period, such as the 2007-08 financial crisis, there are only a handful of modern historical precedents and the outcomes from these diverge significantly. At one extreme there have been sharp recessions that the US has recovered from quickly, such as 1953, and at the other extreme are prolonged slowdowns, such as the Great Depression. Because forecasts in crises are based on so little data, a rise in the probability of a crisis amplifies uncertainty about the direction of the economy. This generates a spike in macro uncertainty.
As well as increasing macro uncertainty, disaster risk causes an increase in disagreement amongst people in the economy. This is where private information comes in. When there is broad agreement about the future path of the economy small differences in information between people don’t matter much. But when disaster risk rises, the range of plausible future outcomes expands and small differences in information are amplified into much larger differences in forecasts. When forecasts diverge there is more disagreement, which is high-order uncertainty. Differences in forecasts also drive differences in the decisions of firms, causing more variation in firm outcomes. This is micro uncertainty.
The fact that agents don’t know the true structure of the economy and continually re-estimate their model amplifies the impact of disaster risk on uncertainty. When agents observe an unexpected event, their model estimates change to accommodate this, and this increases the probability of an extreme outcome. This increases all three types of uncertainty.
While micro, macro and higher-order uncertainty may be conceptually distinct, they share common ties to disaster risk. Since uncertainty shocks are a major avenue of research in the quest to explain business cycles, as well as asset prices and financial crises, a unified understanding of the various forms of belief changes takes us one step further along these paths.
References
Angeletos, M, F Collard, and H Dellas (2014), “Quantifying Confidence,” MIT working paper.
Angeletos, M and J La’O (2014), “Sentiments,” Econometrica, 81(2), 739-779.
Arellano C, Y Bai and P Kehoe (2012), “Financial Frictions and Fluctuations in Volatility,” Federal Reserve Bank of Minneapolis woking paper.
Bachmann, R and C Bayer (2014), “Investment Dispersion and the Business Cycle,” American Economic Review, 104(4), 1392-1416.
Bachmann, R and C Bayer (2013), “‘Wait-and-See’ Business Cycles?,” Journal of Monetary Economics, 60(6), 704–719.
Benhabib, J, P Wang and Y Wen (2015), “Sentiments and Aggregate Demand Fluctuations,” Econometrica, 83(2), 549–585.
Bloom, N (2009), “The Impact of Uncertainty Shocks,” Econometrica, 77(3), 623-685.
Bloom, N, M Floetotto, N Jaimovich, I Sapora-Eksten and S Terry (2012), “Really Uncertain Business Cycles,” NBER working paper 13385.
Christiano, L, R Motto and M Rostagno (2014), “Risk Shocks,” American Economic Review, 104(1), 27-65.
Fajgelbaum, P, E Schaal, and M Taschereau-Dumouchel (2016), “Uncertainty Traps,” Quarterly Journal of Economics, forthcoming.
Gilchrist, S, J Sim and E Zakrajsek (2014), “Uncertainty, Financial Frictions, and Investment Dynamics,” Boston University and Federal Reserve Board working paper.
Jurado, K, S Ludvigson and S Ng (2015), “Measuring Uncertainty,” American Economic Review, 105(3), 1177-1216.
Kozeniauskas, O and L Veldkamp (2016), “The Common Origin of Uncertainty Shocks,” NBER working paper 22384.
Ordonez, G (2011), “The Asymmetric Effects of Financial Frictions,” Journal of Political Economy, 121(5), 844-895.
Pastor, L and P Veronesi (2012), “Uncertainty about Government Policy and Stock Prices,” Journal of Finance, 67(4), 1219-1264.
Schaal, E (2012), “Uncertainty, Productivity and Unemployment in the Great Recession,” Federal Reserve Bank of Minneapolis working paper.
Van Nieuwerburgh, S and L Veldkamp (2006), “Learning Asymmetries in Real Business Cycles,” Journal of Monetary Economics, 53(4), 753–772.
Veldkamp, L (2005), “Slow Boom, Sudden Crash,” Journal of Economic Theory, 124(2), 230-257.
Endnotes
[1] Papers that examine macro uncertainty in theories or measure it empirically include Veldkamp (2005), Fajelbaum, Schaal and Taschereau-Dumochel (2016), Jurado et al. (2015), Bloom et al. (2012), Ordonez (2011) and Pastor and Veronesi (2012).
[2] For micro uncertainty shocks see, for example, Arellano et al. (2012), Christiano et al. (2014), Gilchrist et al. (2014), Schaal (2012), Bachmann and Bayer (2013) and Bachmann and Bayer (2014). The last two papers dispute the importance of these shocks for aggregate activity. Some papers such as Bloom (2009) and Bloom et al. (2012) use micro and macro uncertainty shocks.
[3] On the role of higher-order uncertainty see Angeletos and La'O (2014), Angeletos et al. (2014) and Benhabib et al. (2015).
[4] We measure micro uncertainty as the inter-quartile range of firm earnings growth (data from Bloom et al, 2012), higher order uncertainty as the cross-section standard deviation of GDP growth forecasts (from the Survey of Professional Forecasters), and proxy for macro uncertainty with an uncertainty index constructed by Bloom (2009) using the VIX and VXO. See Kozeniauskas et al. (2016) for more measurement details on all three series.