In modern models of the business cycle, the fluctuations in macroeconomic variables such as output, consumption, and investment are initiated by shocks to exogenous structural disturbances and then magnified and propagated by the economic mechanisms of the model. One example is a productivity disturbance that affects firms’ investment and hiring plans. Another example is a preference disturbance that reflects households’ willingness to consume now as opposed to save for the future. The development of sophisticated Bayesian estimation techniques has generated a surge of papers that estimate fully specified macroeconomic models.1 Important catalysts were Smets and Wouters (2003) and Smets and Wouters (2007).
In this empirical literature, it is very rare that the possibility of misspecification is taken into account.2 Obviously, there are many reasons why a model could be misspecified. For example, assumptions about the market structure, expectation formation, and/or functional forms for objects such as utility functions could be incorrect. In a recent paper (Den Haan and Drechsel 2018), we focus on the possible misspecification of exogenous structural disturbances, the lifeblood of fluctuations in modern business cycle models. The specification of the different structural disturbances is rarely questioned despite their crucial role.3 Moreover, researchers often use a large number of such disturbances for technical reasons.4
The word “disturbance” may indicate it represents a term of an unrestricted or reduced-form nature, like regression error terms. The opposite is true. Researchers have to decide precisely in which equations and how they enter these equations, that is, which economic decision margins they affect and how. Moreover, they are required to write down laws of motion of the structural disturbances.
Dealing with the misspecification and incompleteness of dynamic macroeconomic models is not trivial. To understand this, note that the purpose of estimated macroeconomic models is rarely to obtain a good fit for a time-series model of economic aggregates or have parameter estimates that converge towards a well-defined statistical loss criterion.5 A much more common purpose of the estimation of macroeconomic models is to understand the qualitative aspects and quantitative importance of particular economic mechanisms and to use the estimated model for policy experiments. For this purpose, a correct representation of the empirical model using the true model parameters are needed. Even dealing with incompleteness of the empirical specification is difficult and cannot be taken care of by simply adding regression residuals.6
Severe consequences of misspecified structural disturbances
In Den Haan and Drechsel (2018), we document that the misspecification of a structural disturbance can lead to large distortions in the estimation of macroeconomic models even if that disturbance plays a minor role. Thus, researchers may reach false conclusions about how the economy works and how implied policies impact economic outcomes if they enter the wrong disturbance or enter it incorrectly. We show this using experiments in which we generate data using a known economic model and then estimate the model using a specification that is completely correct except that it features a minor change in how the exogenous structural disturbances affect the economy. Specifically, one disturbance is wrongly excluded and replaced by another. The standard deviation of this wrongly included disturbance is adjusted to ensure it does not play an important role in driving variation in the data. The misspecifications considered are also minor in the sense that they are difficult to detect in data sets with a realistic sample size. Moreover, we use very large data sets to abstract from sampling variation.
This is a dream scenario since the researcher is given lots of data and only one of the many aspects of the empirical model is not specified correctly. Nevertheless, we find that this type of misspecification can lead to severe distortions for parameter estimates as well as implied model properties, such as comovements of economic variables and responses of variables to structural disturbances. In fact, even the sign of the latter two could be wrong.
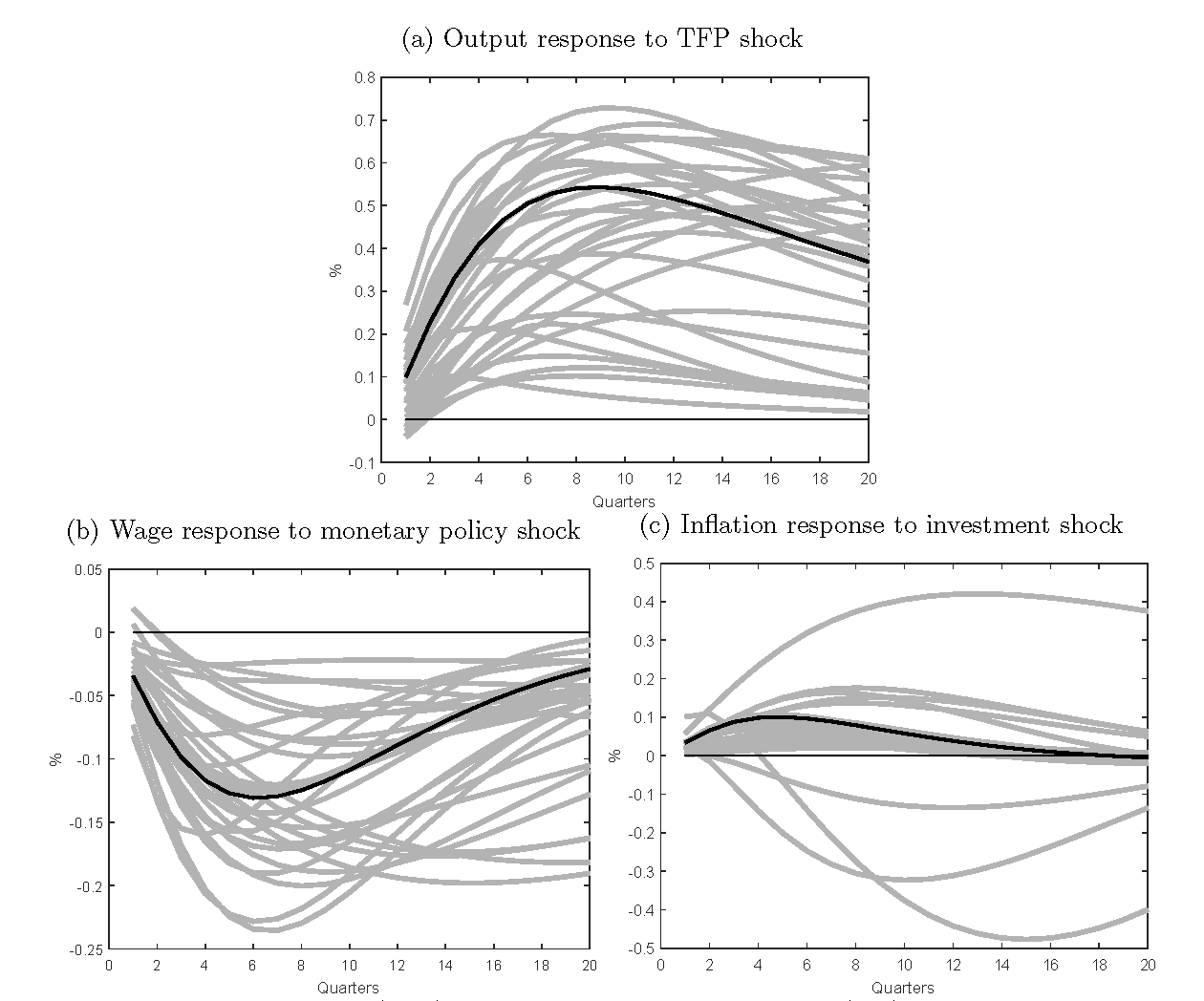
Figure 1 presents impulse response functions (IRFs) of selected model variables to structural shocks that are correctly specified. The true IRF is shown in black, while the grey lines represent IRFs from a set of different estimated models, all slightly misspecified in the way described above. The figure demonstrates that a minor misspecification can have large consequences for the shape and even the sign of the IRFs relative to their true counterpart even for the structural disturbances that are correctly specified. These responses are key characteristics of the model that a researcher would study to draw conclusions about how the economy works.
Figure 1 Impulse response functions according to true (black) and misspecified (grey) empirical models
Agnostic structural disturbances to detect and reduce misspecification
Our paper proposes a novel concept, namely, an agnostic structural disturbance (ASD), which can be used in two ways. First, ASDs can be used to test whether regular structural disturbances are correctly specified. Second, an empirical specification can be enriched by adding ASDs as additional structural disturbances. ASDs are like regular structural disturbances except that they do not impose restrictions on what the initial impact is. Since they are structural disturbances, they are part of the actual economic model and are magnified and propagated according to the mechanisms of the model. Their initial impact, however, is unrestricted and this is where they differ from regular structural error terms. ASDs are not reduced-form error terms!
In an empirical specification with ASDs, the data determine how ASDs affect the economic variables, not the restrictions imposed by the model builder. Thus, ASDs are different from ‘wedges’ (see Chari et al. 2007), which do impose restrictions, for example, by selecting the equations in which a particular wedge enters the model. They are also different from measurement error, as ASDs are part of the economic model and their shocks affect the system through time according to the mechanisms of the model. In Den Haan and Drechsel (2018), we document using Monte Carlo experiments that the ASD procedure is capable of detecting and correcting for misspecification in samples of typical size.
Interpreting ASDs
We also apply the ASD procedure to a well-known business cycle model, the Smets and Wouters (2007) (henceforth, SW) model, to investigate whether its structural disturbances are the correct ones for post-war US data. We find that the SW risk-premium disturbance and the SW investment-specific productivity disturbance are rejected in favour of ASDs. While agnostic in nature, studying the estimated properties of these ASDs allows us to interpret them economically. Specifically, the ASDs of our preferred specification actually generate responses that display some similarities to a SW risk-premium and the SW investment-specific productivity type disturbance. However, our results indicate that they enter the model quite differently than the original SW disturbances, which are not only used by SW but commonly used in the literature.7
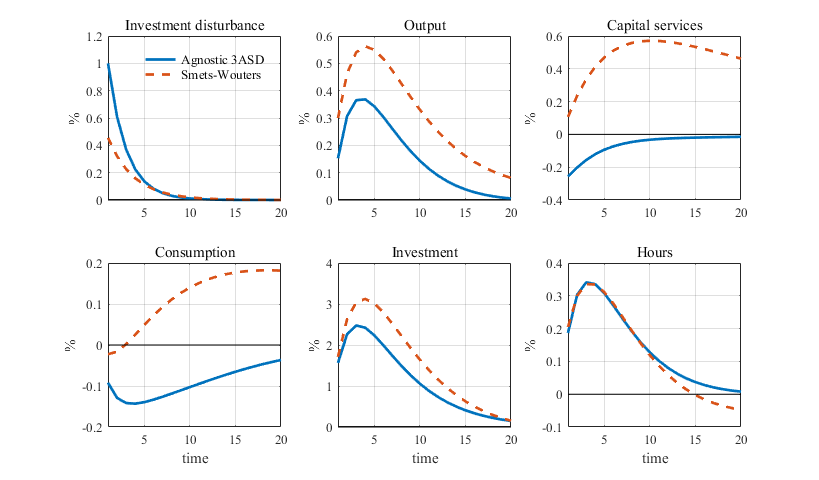
Figure 2 Impulse response functions of an investment disturbance: Smets-Wouters versus agnostic
To illustrate the economic interpretation of ASDs, Figure 2 focuses on the investment-specific disturbance and compares the IRFs for the original SW disturbance and the ASD. A comparison of the IRFs shows that our agnostic investment-specific disturbance stimulates investment just as its SW analogue, but it also goes together with increased depreciation of the existing capital stock. This indicates that an investment-specific productivity shocks goes together with the scrapping of older vintages of capital, a feature that is not part of standard business cycle models. Thus, replacing the original SW disturbance with an ASD not only reduces misspecification of the model, we also gain some economic insight into the actual impact of key driving forces of business cycles.
Concluding comments
It is not complicated to implement our proposed ASD procedure. For example, it is easy to incorporate ASDs in Dynare programs. Our paper contains detailed guidance on how researchers can proceed in practice.
Obviously, ASDs do not take care of all possible misspecification issues. Thus, we consider the inclusion of ASDs to be a minimal necessary step for researchers who do not want to do research under the mistaken belief that misspecification is something that can be ignored.
References
Chari, V V, P J Kehoe and E R McGrattan (2007), “Business Cycle Accounting”, Econometrica 75: 781–836.
Del Negro, M, F Schorfheide, F Smets, and R Wouters (2007), “On the Fit of New Keynesian Models”, Journal of Business and Economic Statistics 25(2): 123–143.
Den Haan, W and T Drechsel (2018), “Agnostic Structural Disturbances (ASDs): Detecting and Reducing Misspecification in Empirical Macroeconomic Models”, CEPR Discussion Paper 13145
Hall, H (1982), “Maximum Likelihood Estimation of Misspecified Models”, Econometrica 50: 1-25.
Smets, F and R Wouters (2003), “An Estimated Stochastic Dynamic General Equilibrium Model of the Euro Area”, Journal of the European Economic Association 1: 1123–1175.
Smets, F and R Wouters (2007), “Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach”, American Economic Review 97: 586–606.
Endnotes
[1] These methods use Monte Carlo Markov Chains (MCMCs) to obtain the posterior distributions of the structural parameters and of other model objects. Although some diagnostic statistics exist, it is not clear what the exact outcomes of these diagnostics have to be for results to be a reliable representation of the true underlying posterior. Nevertheless, it should be standard practice to report these diagnostic statistics which is – strangely enough – not the case.
[2] A notable exception is Del Negro et al. (2007), who develop a methodology for dealing with misspecification. Details on how our proposed method differs from theirs can be found in Den Haan and Drechsel (2018).
[3] When aggregate productivity disturbances were first introduced in the early eighties, they were received with much scepticism, especially the importance of negative shocks. These days, however, the discussion has died out. They are included in virtually all macroeconomic models and neither their existence, nor their modelling is questioned.
[4] Specifically, to avoid a singularity in the estimation one needs as many random driving forces as observables. The practice of simply adding a regression error term to capture the variation in observables not captured by the model cannot be used in the estimation of macroeconomic models. The reason is that these left out elements are correlated with lagged endogenous variables which play a key role in macroeconomic models. Thus, they do not satisfy the required properties of regression residuals.
[5] Thus, one cannot rely on results from the econometrics literature such as those in White (1982).
[6] The claims in this paragraph are explained (in a hopefully intuitive manner) in an accompanying document available at www.wouterdenhaan.com/misspecification.pdf.
[7] Our procedure also selects an additional wage mark-up disturbance.