The dramatic underrepresentation of women in STEM studies, as well as in STEM occupations, has sparked heated debate. Recent evidence shows that the choice of a college major can be as important, or even more important, than the choice of going to college (see e.g. Altonji et al. 2012, or Altonji et al. 2015). For example, Kirkeboen et al. (2016) show that choosing a science versus a humanities major may triple earnings. Maths-intensive majors are often associated with the highest labour market returns, making the choice of college major highly relevant for discussions of gender inequality (Kahn and Ginther 2017, Sloane et al. 2021).
Assessing the impact of the different types of degrees/majors on future labour market outcomes presents important difficulties. To tackle this research question, one must consider that agents are heterogeneous, endowed with their own set of skills and preferences. Consequently, agents are choosing among a potentially large number of alternatives that cannot be ordered in an objective and unambiguous way (Hastings et al. 2013, Kirkeboen et al. 2016).
In a recent paper (Braccioli et al. 2023), we analyse the causal impact of higher education on the labour market success of college graduates. We develop a simple empirical model with three possible choices: not going to college, going to a STEM college, and going to a non-STEM college. To estimate the labour market returns of these educational alternatives, we bring the model to data using confidential survey data for Italy combined with administrative information about the founding dates of all Italian universities and faculties. We build upon literature that uses distance from college as an instrumental variable for college enrolment (Card 1995, Nybom 2017). Specifically, we model college choice as a function of a four-valued discrete variable whose categories indicate proximity to colleges offering STEM and/or non-STEM programmes. In the empirical application, a college is ‘near’ to an individual if it is in the province of residence at the age of completing compulsory education; otherwise, it is ‘far’.
As there is no natural ordering of the treatments or the instrument values, we adopt a novel methodology to identify the distribution of response types and treatment effects in a multiple unordered discrete choice setting (Heckman and Pinto 2018). While a total of 81 response types are theoretically possible, we rule out the types that appear irrational based on a simple model of rational choice. For example, if an individual was already willing to go to a STEM college when it was far, then we argue she should not change her mind when the STEM college becomes closer, holding constant the distance to non-STEM colleges. We exclude all such irrational response types and eventually retain only eight, which are sufficiently few to allow the identification of their full distribution and of the treatment effects of several interesting policy interventions.
We show that college proximity is strongly correlated with college choices. We find that the group that is the most responsive to college proximity are women at the margin between choosing a STEM education and not attending college. This group is about one-third the size of current female STEM graduates, so policies that target them may have a large effect on the gender gap in STEM. We further use the estimated treatment effects and response type probabilities to evaluate the effects of a hypothetical reform which creates a new STEM school in any Italian province that does not have one. This simulation is motivated by the current lively debate, both in academia and in policy circles, which suggests that there might be substantial unmet demand for STEM graduates and that women might be especially discouraged from undertaking this type of study due to a variety of cultural and institutional constraints. In Italy, such a reform would imply the creation of 48 new STEM schools.
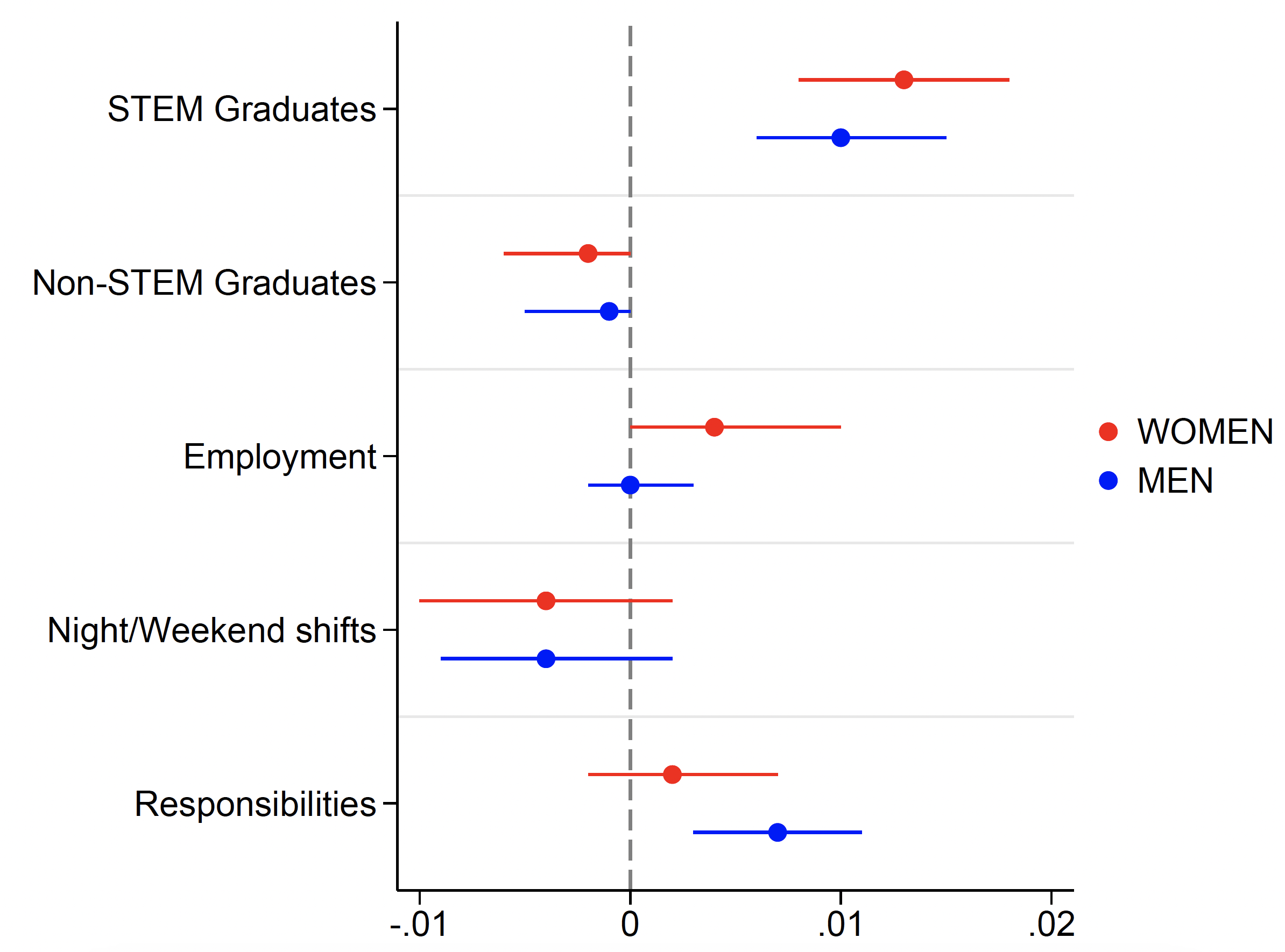
Figure 1 Average treatment effects of STEM expansion
Note: The figure reports the average treatment effects (ATE) of a hypothetical expansion of the supply of STEM education, which consists of creating a new STEM school in any Italian province that does not have one. The outcomes considered are: the share of STEM graduates, the share of NON-STEM graduates, the share of employed persons, the share of employed persons reporting working on night and/or weekend shifts, the share of employed persons reporting having the responsibility of coordinating the work of others.
Results from the simulation suggest that the policy would increase the share of STEM graduates in the population by 1.1 percentage points, which corresponds to an 18% increase over the baseline share of approximately 6.1%. Most of this increase comes from those who would choose not to go to college in the absence of the policy, and a small share (0.2%) are individuals who would switch to STEM from non-STEM subjects. Figure 1 shows that this effect is stronger for women than for men, so the reform would result in narrowing the gender gap in STEM by about 20%. Further, we find evidence that such a reform would increase female employment by about half a percentage point, while having no significant effect on male employment. Our results further suggest that working conditions would generally improve for both men and women, as they would both be more likely to work in positions of responsibility (i.e. having the responsibility to coordinate the work of others) and be less likely to work during weekends or at night.
We believe that our results can be interpreted quite generally. The type of variation in college proximity that we exploit broadly corresponds to the choice of commuting rather than moving residence, which entails a difference in living costs of about 40%. Hence, our results can be informative about a broad set of policies aimed at reducing the cost of college, and they indicate that such policies have the potential to substantially reduce the gender gap in STEM education and in labour market outcomes. Furthermore, our findings can be informative for the design of policies aimed at increasing the share of women in STEM. Many such policies are currently targeted to women at the margin between STEM and non-STEM education and our results suggest that it might be more effective to target a different group – that is, women who hesitate between undertaking a STEM programme and not going to college at all.
References
Altonji, J G, E Blom and C Meghir (2012), “Heterogeneity in human capital investments: High school curriculum, college major, and careers”, Technical Report 1, July.
Altonji, J G, P Arcidiacono and A Maurel (2015), “The analysis of field choice in college and graduate school: Determinants and wage effects”, NBER Working Paper 21655.
Braccioli, F, P Ghinetti, S Moriconi, C Naguib and M Pellizzari (2023), “Education expansion, college choice and labour market success”, CEPR Discussion Paper 18712.
Card, D (1995), Discussion of “Using Geographic Variation in College Proximity to Estimate the Return to Schooling”, in Aspects of labour market behaviour: essays in honour of John Vanderkamp, University of Toronto Press.
Hastings, J S, C A Neilson and S D Zimmerman (2013), “Are some degrees worth more than others? Evidence from college admission cutoffs in Chile”, NBER Working Paper 19241.
Heckman, J J, and R Pinto (2018), “Unordered monotonicity”, Econometrica 86(1): 1–35.
Kahn, S and D Ginther (2017), “Women and STEM”, NBER Working Paper 23525.
Kirkeboen, L J, E Leuven and M Mogstad (2016), “Field of study, earnings, and self-selection”, Quarterly Journal of Economics 131(3): 1057–1111.
Nybom, M (2017), “The distribution of lifetime earnings returns to college”, Journal of Labor Economics 35(4): 903–52.
Sloane, S M, E G Hurst and D A Black (2021), “College majors, occupations, and the gender wage gap”, Journal of Economic Perspectives 35(4): 223–48.