International supply chains are transforming the world.
- They revolutionised development options facing poor nations – now they can join supply chains rather than having to invest decades in building their own.
Astoundingly fast industrialisation is the result for developing nations who have chosen the right policies and have a high-tech neighbour.
- Offshoring of labour-intensive manufacturing stages and the attendant international mobility of firm-specific technology launched era-defining growth in emerging markets.
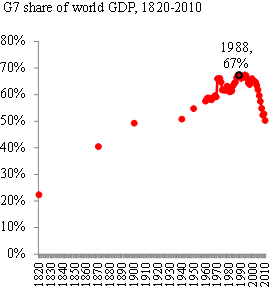
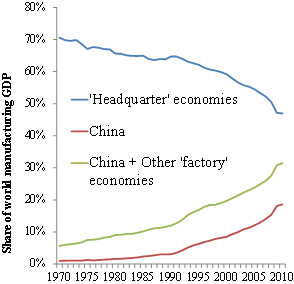
Historic income gaps are narrowing as the North de-industrialises and the South industrialises (Deband 2006) -- a reversal of fortunes that constitutes perhaps the most momentous global economic change in the last 100 years. As Figures 1 and 2 show, this is happening very quickly.
Figure 1. Reversal of the big income divergence
Source: World Databank from 1960; Maddison pre-1960.
Note: Pre-1960, G7=W Europe, US, Canada, Australia & N Zealand
Figure 2. G7 share of global manufacturing
Source: UN online database, unstats.un.org
Note: HQ economies = G7; other factory economies = Korea, Malaysia, Thailand, Singapore, India, Indonesia, Brazil, Mexico, and Turkey.
The rise in global supply chains is also transforming international trade patterns, as trade in intermediates becomes more and more important. This change in trade patterns requires a rethinking of the standard workhorse model to understand trade flows, i.e. the gravity model.
The gravity model
A standard tool in assessing bilateral trade’s causes and effects is the gravity model. In a recent paper (Baldwin and Taglioni 2011), we show that the gravity equation is not valid for trade flows where trade in parts and components is important.
The basic point is simple.
- The standard gravity equation is derived from a consumer expenditure equation with the relative price eliminated using a general equilibrium constraint (Anderson 1979, Bergstrand 1985, 1989, 1990).
- As such the standard formulation and empirical application (Anderson and van Wincoop 2003) is best adapted to explaining trade in consumer goods.
When consumer trade dominates, the GDP of the destination nation is a good proxy for consumer demand; the GDP of the origin nation is a good proxy of its total supply.
- When international trade in intermediate goods dominates, the use of GDPs for the supply and demand proxies is less appropriate.
Consider, for instance, the determinants of Thai imports of auto parts from the Philippines. The standard formulation would use Thai GDP to explain Thailand’s import demand, however, the underlying demand for parts is generated by Thai gross production of autos, not its value-added in autos. As long as the ratio of local to imported content does not change, value added is a reasonable proxy for gross output, so the standard regression is likely to give reasonable results. However, for regions where production networks are emerging, value added can be expected to be a poor proxy for consumer demand.
We use the Krugman and Venables (1996) model to explore the impact of allowing intermediates trade in the gravity model. The key differences show up in the definition of the economic “mass” variables since purchases are now driven both by consumer demand (for which income is the demand shifter) and intermediate demand (for which total production is the demand shifter).
This observation generates a number of testable hypotheses.
- The estimated coefficient on the GDPs should be lower for nations where parts trade is important, and should fall as the importance of parts trade rises.
- As vertical-specialisation trade has become more important in recent years, the GDP point estimates should now be lower.
- In those cases where the GDPs of the trade partners lose explanatory power, bilateral trade should be increasingly well explained by demand in third countries.
For example, China’s imports should shift from being explained by China’s GDP to being explained by its exports to, say, the US and the EU. There are two ways of phrasing this hypothesis. First, China’s imports are a function of its exports rather than its own GDP. Second, China’s imports are a function of US and EU GDP rather than its own, since US and EU GDP are critical determinants of their imports from China.
Gravity when parts-and-components trade is important
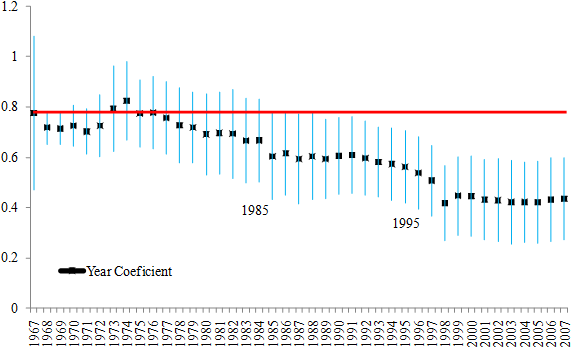
To examine these conjectures empirically, we estimate the standard gravity model for different sets of countries and sectors for a panel that spans from 1967 to 2007, allowing for yearly interaction terms. The results for Factory Asia countries, displayed in Figure 3, show the GDP coefficients falling over time, with two clear breaks in the estimated coefficients, 1985 and 1998. The timing and direction of these structural changes are very much in line with the literature on the internationalisation of production.
Figure 3. GDP coefficients for Factory Asia countries, 1967-2008
Notes: Estimated mass-elasticity coefficients with year interactions and pair fixed effects (as in 10). High and low bars show plus/minus 2 standard errors; Factory Asia countries: Japan, Indonesia, Republic of Korea, Malaysia, Thailand, and Taiwan.
These results are highly suggestive. On data that is known as being dominated by parts and components trade, we find the mass-variable coefficient moving in the expected direction. However, on data where this sort of production fragmentation is not widely viewed as having been important, we find that that mass point-estimates are stable over time.
What’s more, when we include the ratio of intermediates to total trade as a regressor, both on its own and – more importantly – as an interaction with the economic mass variable, we find importer GDP matters less for countries that import a larger share of intermediates).
A search for mass proxies when intermediates are important
Theory suggests that the perfect solution would require data on total costs to proxy for demand for intermediates imports. If the economy is reasonably competitive, gross sales would be a good proxy for the total costs. Unfortunately, such data are not available for a wide range of nations especially the developing nations where production fragmentation is so important. On the mass variable for the origin nation, theory suggests that we use gross output rather than value added. Again such data are not widely available.
To find a proxy, we start with the destination nation’s mass variable. The total flow of goods is the sum of consumer goods, whose demand depends upon the importing nation’s GDP and intermediate goods whose demand depends upon the total costs of the sector buying the relevant intermediates. This suggests a first measure that adds imports of intermediates to GDP .
To proxy for supply inthe origin nation, we are trying to capture gross output. Our proposed measure for output size adds purchases of intermediate inputs from all sources (except from itself due to a lack of data) to value added in manufacturing.
Using these proxies we are able to fit the data more precisely that with standard gravity equations… The R-squares, which measure the share of the data that can be explained by the model, increase from … to … etc… etc…
Why do incorrectly-specified mass variables matter?
A large number of gravity studies focus on variables that vary across country pairs – say free trade agreements, cultural ties, or immigrant networks. The most recent of these studies employ estimators that control for the mass variables with fixed effects. Such studies do not suffer from mass-variable mis-specification and so are unaffected by our critique. There are however a number of recent studies – especially concerning the ‘distance puzzle’ that do proxy for the production and demand variables with GDP. It is these studies that our work speaks to.1
Since most of these studies are concerned with a broad set of nations and commodities, the mis-specification of the mass variable probably has a minor impact on the results – as the findings of Bergstrand and Egger (2010) showed. More worrying, however, is the use by authors that focus on trade in parts and components such as Athukorala and Yamashita (2006), Kimura et al (2007), Yokota and Kazuhiko (2008), and Ando and Kimura (2009). These papers all use the consumer good version of the gravity model to describe parts and components trade and thus have mis-specified the mass variable.
Summary
We present empirical evidence that the standard gravity model performs poorly by some measures when it is applied to bilateral flows where parts and components trade is important.
Our paper also provides a simple theoretical foundation for a modified gravity equation that is suited to explaining trade where international supply chains are important. Finally we suggest ways in which the theoretical model can be implemented empirically.
Our fix is a long way from perfect, but we hope it shows other researchers that it would be worth looking for something that works even better!
References
Debande, Oliver (2006). “De-industrialisation”, European Investment Bank Papers, Volume 11 No 1.
Anderson, James and Eric van Wincoop (2003). "Gravity with Gravitas: A Solution to the Border Puzzle," American Economic Review, vol. 93(1), pages 170-192,
Anderson, James (1979), “The theoretical foundation for the gravity equation,” American Economic Review 69, 106-116.
Ando, Mitsuyo and Fukunari Kimura (2009). “Fragmentation in East Asia: Further Evidence”, ERIA Discussion Paper Series, DP-2009-20, October.
Athukorala, P. and N. Yamashita (2006), “Production Fragmentation and Trade Integration: East Asia in a Global Context”, The North American Journal of Economics and Finance, 17, 3, 233-256.
Baldwin, Richard and Daria Taglioni (2007). “Gravity for dummies and dummies for gravity equations” NBER WP 12516, published as "Trade effects of the euro: A comparison of estimators”, Journal of Economic Integration, 22(4), December, pp 780–818. 2007.
Bergstrand, Jeffrey (1985), ”The Gravity Equation in International Trade: Some Microeconomic Foundations and Empirical Evidence,” Review of Economics and Statistics, 1985, 67:3, August, pp. 474-81.
Bergstrand, Jeffrey and Peter Egger (2010) “A General Equilibrium Theory for Estimating Gravity Equations of Bilateral FDI, Final Goods Trade and Intermediate Goods Trade”, in S. Brakman and P. Van Bergeijk (eds) The Gravity Model in International Trade: Advances and Applications, Cambridge University Press, New York.
Grossman, Gene M. and Esteban Rossi-Hansberg (2008). "Trading Tasks: A Simple Theory of Offshoring," American Economic Review, vol. 98(5), pages 1978-97, December.
Kimura, F., Y. Takahashi and K. Hayakawa (2007), “Fragmentation and Parts and Components Trade: Comparison between East Asia and Europe”, The North American Journal of Economics and Finance, 18, 1, 23-40.
Kimura, Fukunari, Yuya Takahashi and Kazunobu Hayakawa (2007). "Fragmentation and parts and components trade: Comparison between East Asia and Europe," The North American Journal of Economics and Finance, vol. 18(1), pages 23-40.
Krugman Paul and Anthony Venables (1996) “ Intergration, specialisation, and adjustment” European Economic Review 40, pp. 959-967.
Yi, K-M (2003). “Can Vertical Specialization Explain the Growth of World Trade?” The Journal of Political Economy, Vol. 111, No. 1 (Feb.), pp. 52-102.
Yokota, Kazuhiko (2008). “Parts and Components Trade and Production Networks in East Asia -A Panel Gravity Approach”, Chapter 3 in Hiratsuka & Uchida eds., Vertical Specialization and Economic Integration in East Asia, Chosakenkyu-Hokokusho, IDE-JETRO, 2008.
1For example, Rauch (1999), Brun et al (2005), Berthelon and Freund (2008), and Jacks et al (2008) use GDP as the mass variable when they decompose the change in the trade flow into the effects of income changes and trade cost changes; Anderson and Van Wincoop (2003) also use GDP as the mass variable in one of their estimation techniques.