A vast empirical literature has shown that the firm size distribution is typically characterised by a power-law right tail, comprised of a relatively small number of large firms. Power-law tails emerge as a consequence of Gibrat’s law, which states that growth rates are independent of firm size. Accordingly, the fact that a power-law tail is found only for very large firms implies that Gibrat’s law breaks down for small and medium-sized firms. In order to investigate the breakdown of Gibrat’s law, we must consider that firm growth rates are mutually dependent since firms are connected through supply and commercial credit network.
Two different but interconnected streams of research stress the relevance of both the firm size distribution and supply network connections to the macroeconomy. On the one hand, Gabaix (2011) has shown that the existence of a power-law tail in the firm size distribution implies that microeconomic shocks cannot average to zero, given the macroeconomic relevance of the largest firms (the ‘granular hypothesis’). On the other hand, Acemoglu et al. (2012) demonstrated that firm-level shocks have aggregate relevance since they are transmitted from one sector to another through the supply network.
As a consequence, a causal chain emerges between firm size distribution, firm growth rates, and supply networks: the structure of the supply network determines the mechanism of transmission of shocks, which in turn affects the growth of firms and, finally, the firm size distribution. In Japan, the existence of a relationship between the firm size distribution and the supply network seems to be confirmed by the fact that small and medium firms are suppliers to large firms (e.g. Fujiwara 2020).
In new research (Di Guilmi and Fujiwara 2022), we investigate whether the observed breakdown of Gibrat’s law in Japan for small and medium-sized firms depends on the structure of the supply network and on the position of firms within the network.
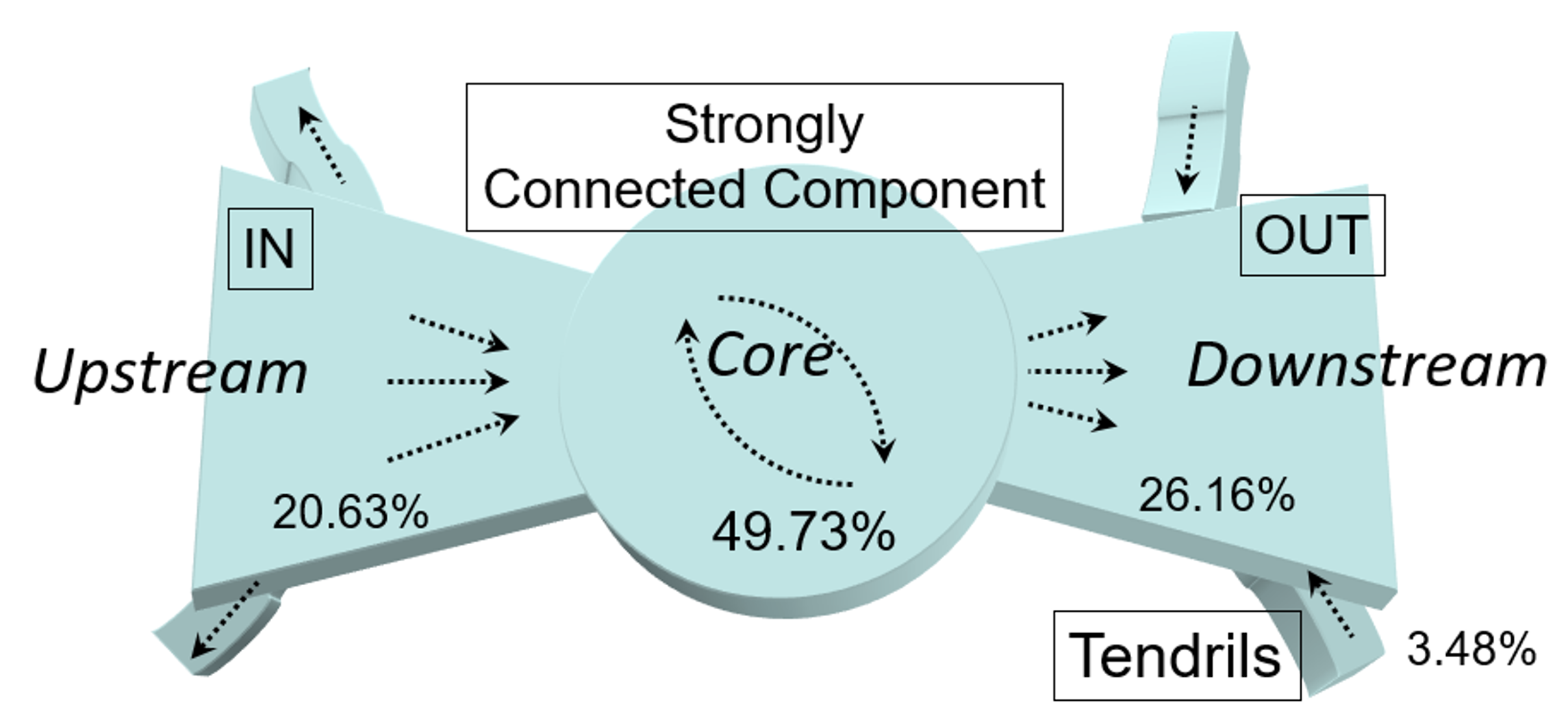
We present an empirical study of the Japanese production network based on a dataset comprised of more than one million firms and the millions of supplier-customer relationships linking them. The network can be regarded as a graph, mathematically speaking, which consists of firms as nodes and edges with direction from suppliers to customers. The particular structure of the giant graph of a production network is usually referred to as a ‘bow-tie’ (see Figure 1). We can identify a core (defined by the strongly connected component and accounting for nearly 50% of firms) in which one or more directed paths of edges are present for any pair of firms. The core involves the majority of goods and services circulated. Additionally, there exists an upstream component (indicated by ‘IN’ in the figure) comprising firms mainly supplying the core (including the supply of raw materials). Finally, the downstream component (‘OUT’) is comprised of firms that demand goods and services mainly from the core. Importantly, the macroscopic line of production is not hierarchical or one-way from upstream to downstream, but instead is circular.
Figure 1 Bow-tie structure of the Japanese production network
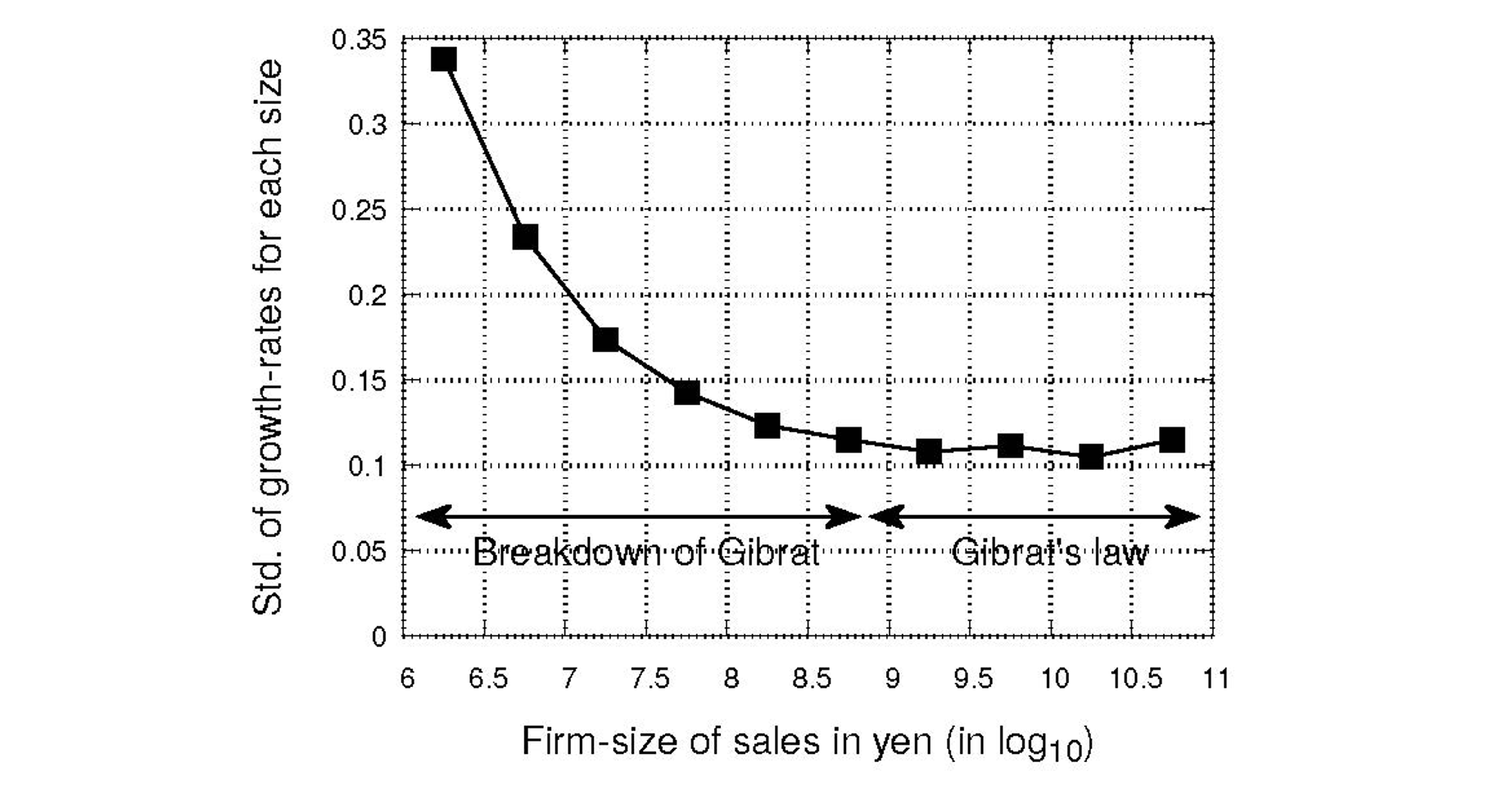
Also in Japan, as in many other countries, the firm size distribution displays a power-law tail with ‘a few giants and many dwarfs’. Furthermore, examining individual firm growth (defined by annual change of size), one can observe that Gibrat’s law holds for the regime of large firms, while it breaks down for small and medium firms (see Figure 2). Fujiwara and Aoyama (2010) verify from the production network data that in the manufacturing sector, for example, a large firm often has many suppliers and customers that are small and medium-sized firms. As a consequence, one can expect that a large downstream firm experiencing a demand shock is able to pass its effects onto smaller suppliers, affecting their growth. This shock transmission can be at the root of the breakdown of Gibrat’s law for small and medium-sized firms.
Figure 2 Dependence of standard deviation of growth-rate for the firms binned in different sizes, logarithmically equal-spaced, for Japan
In order to test this hypothesis, in a recent paper (Di Guilmi and Fujiwara 2022) we propose a network model that borrows from Dhyne et al. (2019). Our model is set up to reproduce (in scale) the bow-tie structure of the real Japanese network. The market power of each firm is proxied by their ability to fix the price above their production costs, which depends on the elasticity of their customer’s demand and their position in the network, as upstream firms’ price changes are likely to create higher order effects.
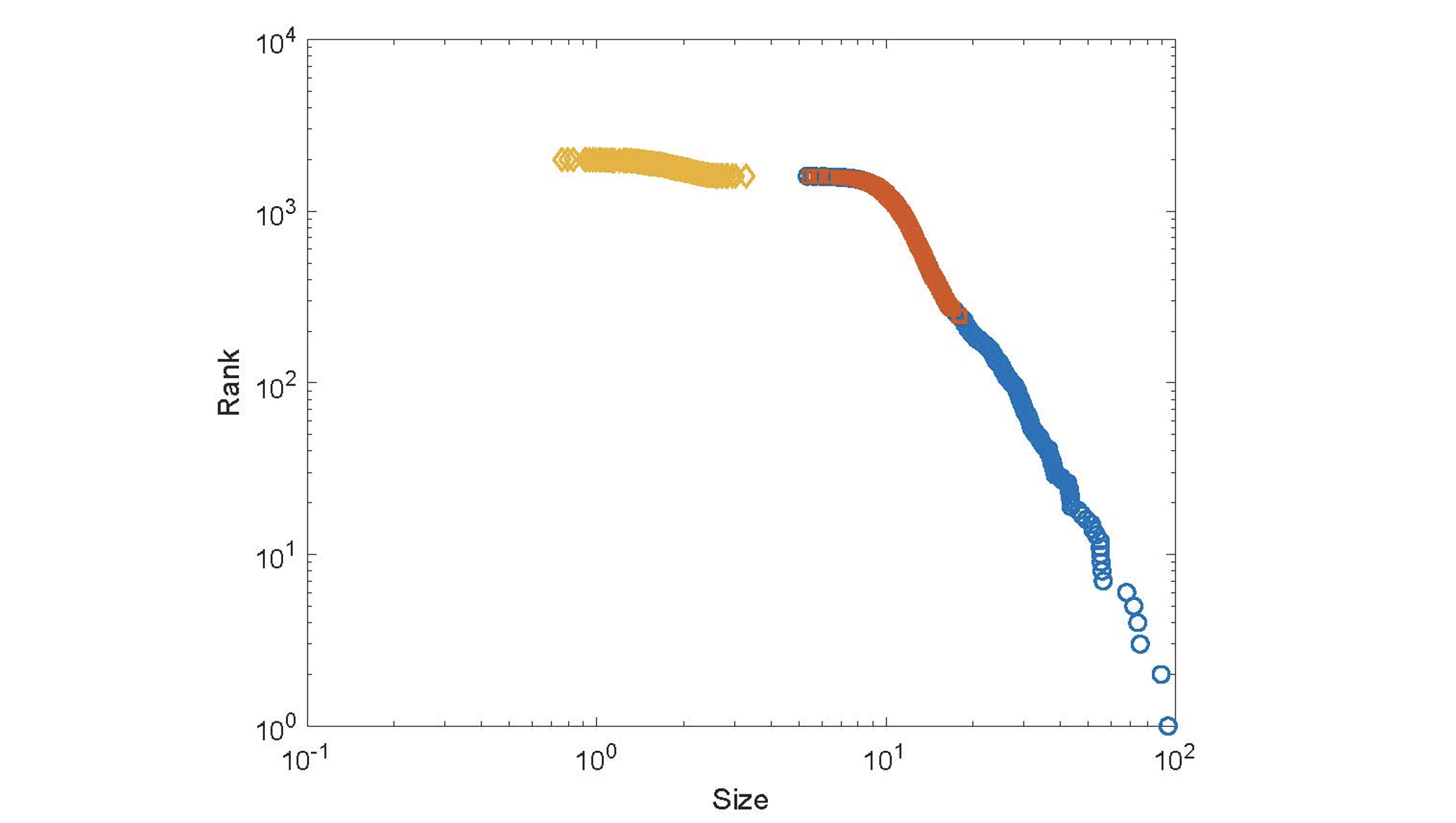
The model is simulated in order to gain some understanding of how the transmission of volatility through the network leads to the emergence of power-law tails. Firms follow the same behavioural rules, have the same production technology, and are subject to independent and identically distributed productivity shocks. The network is static: the links are stochastically created at the beginning of the simulation in order to reproduce the structure of the real network (Figure 1). Initial conditions are equal for all firms but during the simulations a power law distribution emerges (Figure 3) in which downstream firms are larger and therefore located in the right tail of the firm size distribution. The results are confirmed by Monte Carlo replications.
Figure 3 Zipf plot of the firm size distribution generated by the model simulations
Note: Blue circles: ‘OUT’, red circles: ‘Giant strongly connected component’ (GSCC), yellow circles: ‘IN’
Simulating a sizable export shock (-30%, roughly the size of the Great Recession shock) in the second last period of the simulation over 100 Monte Carlo replications, the changes in the medians of the distributions of growth rates for OUT, ‘Giant strongly connected component’ (GSCC), and IN firms are, respectively -0.0373, -0.0944, and -0.1113. The shock initially hitting OUT firms is clearly amplified and eventually generates a larger effect for upstream firms. This set of results confirms the hypothesis that downstream demand shocks are amplified in the supply chain, leading to the breakdown of Gibrat’s law for upstream firms and to the power-law tail in the firm size distribution for downstream firms.
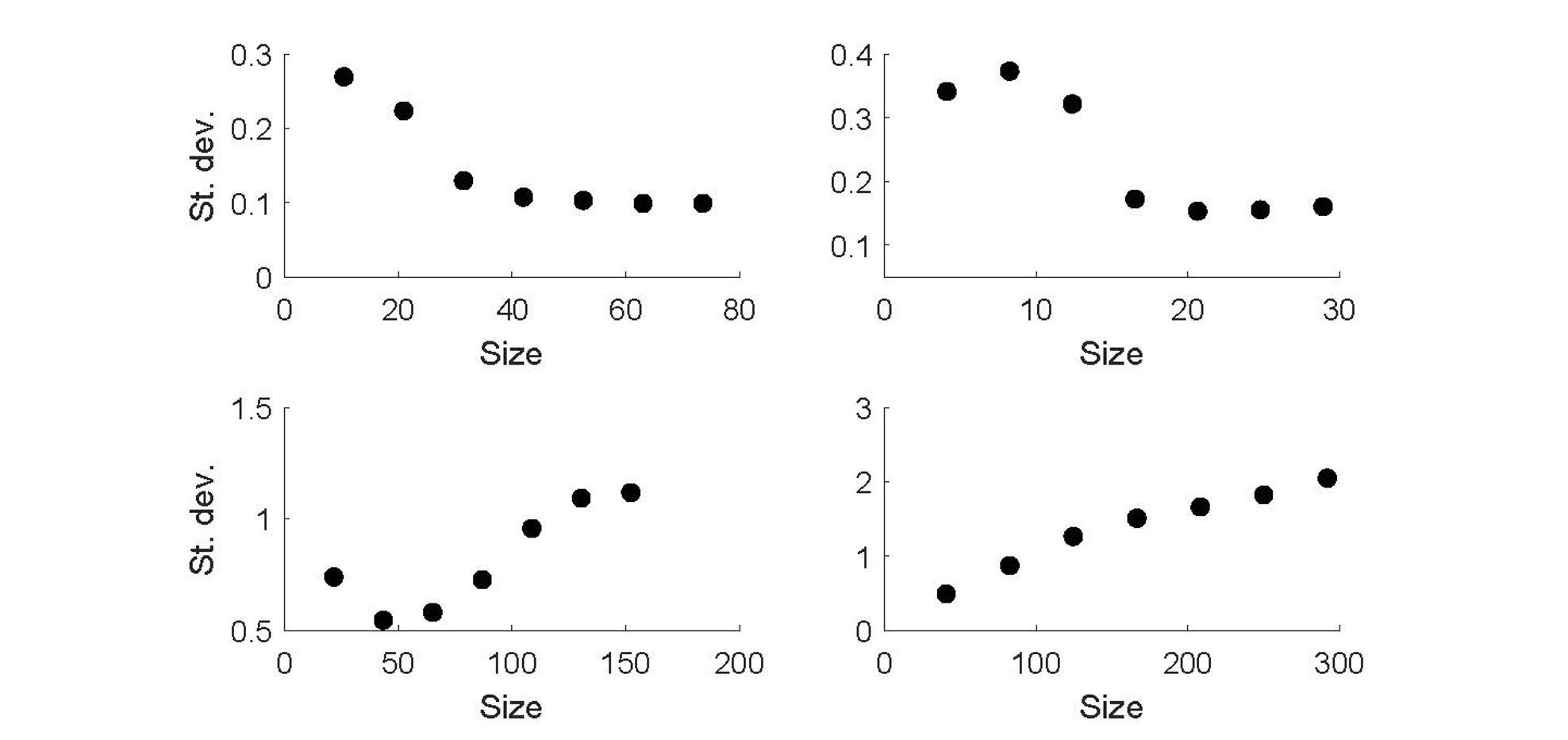
Counter-factual computational experiments are performed in order to evaluate the role of network structure and market power. The top-left panel of Figure 4 reproduces the pattern shown in Figure 2, identifying a scaling regime for small firms and a Gibrat regime for large firms in the relationship between firm size and growth volatility. Each dot in the plot represents the standard deviation in growth rates for each bin of the firm size distribution. A negative relationship is identifiable for small firms, while no apparent correlation can be detected for the largest ones. Hence, Gibrat’s law applies for the largest firms, while it does not hold for the smallest firms, which are upstream in the supply chain. In the top-right panel, elasticity in the intermediate-goods market is higher, implying that suppliers have relatively less market power. Besides the general increase in volatility, the most evident effect is the reduction of Gibrat’s range, since only for the top four bins does volatility not change with size. The general reduction in size compared to the blue and black distributions depends on macro effects, since the tighter market compresses profits and negatively impacts the final consumption demand. However, a power-law tail in firm size distribution still exists.
Since in the model the competitiveness of firms is stochastic, higher elasticity of substitution implies larger expected readjustments for upstream firms, as highly price-sensitive customers redistribute their purchases towards the cheaper suppliers to a larger extent. The numerical simulations are likely to underestimate the extent of the redistribution of demand, since the network is static and abstracts from the complete substitution of less efficient suppliers.
The bottom panels In Figure 4 present the results of a counterfactual experiment, in which the model is simulated in an almost perfect hierarchical network (excluding therefore any circular or upward link). In this setting, the standard deviation in growth rates generally appears to increase with size. When the elasticity in the intermediate goods market is higher, the relationship is monotonic. As a consequence, small firms are no longer necessarily located upstream and, accordingly, the dynamics of upward transmission of shocks changes. As a result, a clear power-law distribution in the right tail is no longer evident.
Figure 4 Size versus standard deviation of sales for all firms as generated by the model simulations (average over 100 Monte Carlo replications)
Note: Upper panels: baseline bow-tie network structure; lower panels: hierarchical network; left panels: demand elasticity larger for intermediate goods than for consumption goods; right panels: same elasticity in both markets.
The analytical solution of the model shows that the demand of upstream firms is likely to be more volatile than the final demand when downstream firms are relatively larger, when individual productivity is more volatile, and when the structure of the network is more complex. Given that in Japan downstream firms are typically larger and the structure of the network is complex, the model predicts that a downstream shock is amplified as its effects are transmitted upward through the different sections of the supply network.
The results highlight a possible drawback of the interconnectedness and diversification in complex network structures as the high number of connections exposes suppliers to a wider range of idiosyncratic firm-level shocks and can therefore amplify micro-level volatility in case of variations in the final demand.
In terms of aggregate outcomes, this sort of ‘upward snowball effect’, as volatility is transmitted to suppliers, can lead to an under-estimation of the overall impact of demand shocks. The first-order or direct effect of demand shocks determines the reduction in output for downstream firms and as such it is accounted for in GDP. However, since the particular mechanism of amplification of shocks that we identify shapes firm size distribution, it also indirectly affects the macroeconomic dynamics because of the “granular hypothesis” (Gabaix 2011). In other words, demand shocks can affect the economy directly through the reduction in output for downstream firms (which is recorded in the GDP) and indirectly by shaping firm size distribution. In particular, they alter the size of the power-law tail and, as a consequence, the applicability of the granular hypothesis and the way in which micro-level shocks affect the macroeconomy.
To conclude, our empirical and theoretical analysis has shown the following. The Japanese supply network has a bow-tie structure in which firms located in the upstream layers display a larger volatility in their growth rates. As a consequence, Gibrat's law breaks down for upstream firms, whereas downstream firms are more likely to be located in the power-law tail of the size distribution. This pattern is determined by the amplification of demand shocks hitting downstream firms. The magnitude of this amplification increases with a more complex network structure and higher market power of downstream firms. In an almost perfectly hierarchical network, the power-law tail in firm size distribution disappears.
Editor’s note: The main research on which this column is based (Di Guilmi and Fujiwara 2022) first appeared as a Discussion Paper of the Research Institute of Economy, Trade and Industry (RIETI) of Japan.
References
Acemoglu, D, V M Carvalho, A Ozdaglar and A Tahbaz-Salehi (2012), “The Network Origins of Aggregate Fluctuations”, Econometrica 80(5): 1977-2016.
Dhyne, E, G Magerman and A K Kikkawa (2019), “Imperfect Competition in Firm-to-Firm Trade”, Universite Libre de Bruxelles Working Paper.
Di Guilmi, C and Y Fujiwara (2022), “Does the Supply Network Shape the Firm Size Distribution? The Japanese case”, Research Institute of Economy, Trade and Industry of Japan, Discussion Paper 22-E-082.
Fujiwara, Y (2020), “Firms Growth, Distribution, and Non-Self Averaging Revisited”, in H Aoyama, Y Aruka and H Yoshikawa (eds), Complexity, Heterogeneity and the Methods of Statistical Physics in Economics: In memory of Masanao Aoki, Springer.
Fujiwara, Y and H Aoyama (2010), “Large-scale structure of a nation-wide production network”, European Physical Journal B 77(4): 565-580.
Gabaix, X (2011), “The granular origin of aggregate fluctuations”, Econometrica 79(3): 733-772.