There are considerable lags in the effects of monetary policy on the economy (e.g. Christiano et al. 1999, Giannone et al. 2019, Jarociński and Karadi 2020, Schnabel 2023). That is why the mandate of the ECB is to maintain price stability over the medium term. This medium-term orientation implies that sources of fluctuations that only temporarily affect inflation can potentially be ignored. In contrast, more persistent driving forces may have an impact on monetary policy decisions. Inflation forecasts identify which effects are persistent and are therefore a key input for these decisions.
Economic forecasts are surrounded by uncertainty and, rather than relying on precise ‘point forecasts’, policy decisions hinge on ‘density forecasts’. These capture the likelihood of different potential future ‘risk’ scenarios.
Modelling inflation dynamics in the euro area is challenging, owing to the many potential drivers and the difficulty in capturing their relationship with inflation dynamics (e.g. Koester et al. 2021). One key point is whether inflation dynamics are well-characterised by linear relationships with their many potential determinants. The assumption of linearity means that a change in an inflation determinant, such as wages, always implies a change in inflation in the same fixed proportion to the change in wages – regardless of the economic conditions prevailing at the time.
The Eurosystem modelling toolbox consists mostly of linear models, as highlighted in the description of the economic analysis provided in the context of the strategy review (Darracq Pariès et al. 2021). However, economic theory argues that inflation dynamics are characterised by non-linearity.
For example, in response to large shocks firms may change their prices much faster and by proportionately larger amounts than they would in response to smaller shocks (e.g. Cavallo et al. 2023).
Using machine learning for density forecasting
In Lenza et al. (2023), we describe a forecasting model for headline and core inflation
that captures potentially very general forms of non-linear inflation dynamics. The model is borrowed from the machine learning literature and is called the quantile regression forest (QRF; Meinshausen 2006), which is a variant of the popular random forest of Breiman (2001).
Given its success at forecasting macroeconomic variables (e.g. Medeiros et al. 2021, Clark et al. 2023), this methodology is gaining ground in the applied economics literature and has also attracted the interest of policymakers. For the potential determinants of inflation, we chose a set of 60 variables, covering a range of measures of inflation expectations, cost pressures, real activity and financial variables.
How do our forecasts compare with those from a linear model?
We find that for core inflation, the non-linear model is generally more accurate than the linear model, though only by a small margin. For headline inflation, the non-linear model is better able to capture the prolonged period of low inflation before and during the Covid-19 pandemic – but it is outperformed by the linear model during the Great Recession and its aftermath. We conclude that euro area core inflation dynamics can be characterised by mild non-linearity, while the evidence for non-linearity in headline inflation dynamics is less compelling. This suggests that the dynamics in the energy and food components of consumer prices, which are part of headline inflation but not core inflation, are broadly linear. Consequently, especially during periods of high commodity price volatility, the energy and food components of headline inflation tend to overshadow the mild non-linearity observed in core inflation.
Our model allows us to break forecasts down into the marginal contributions of the different variables.
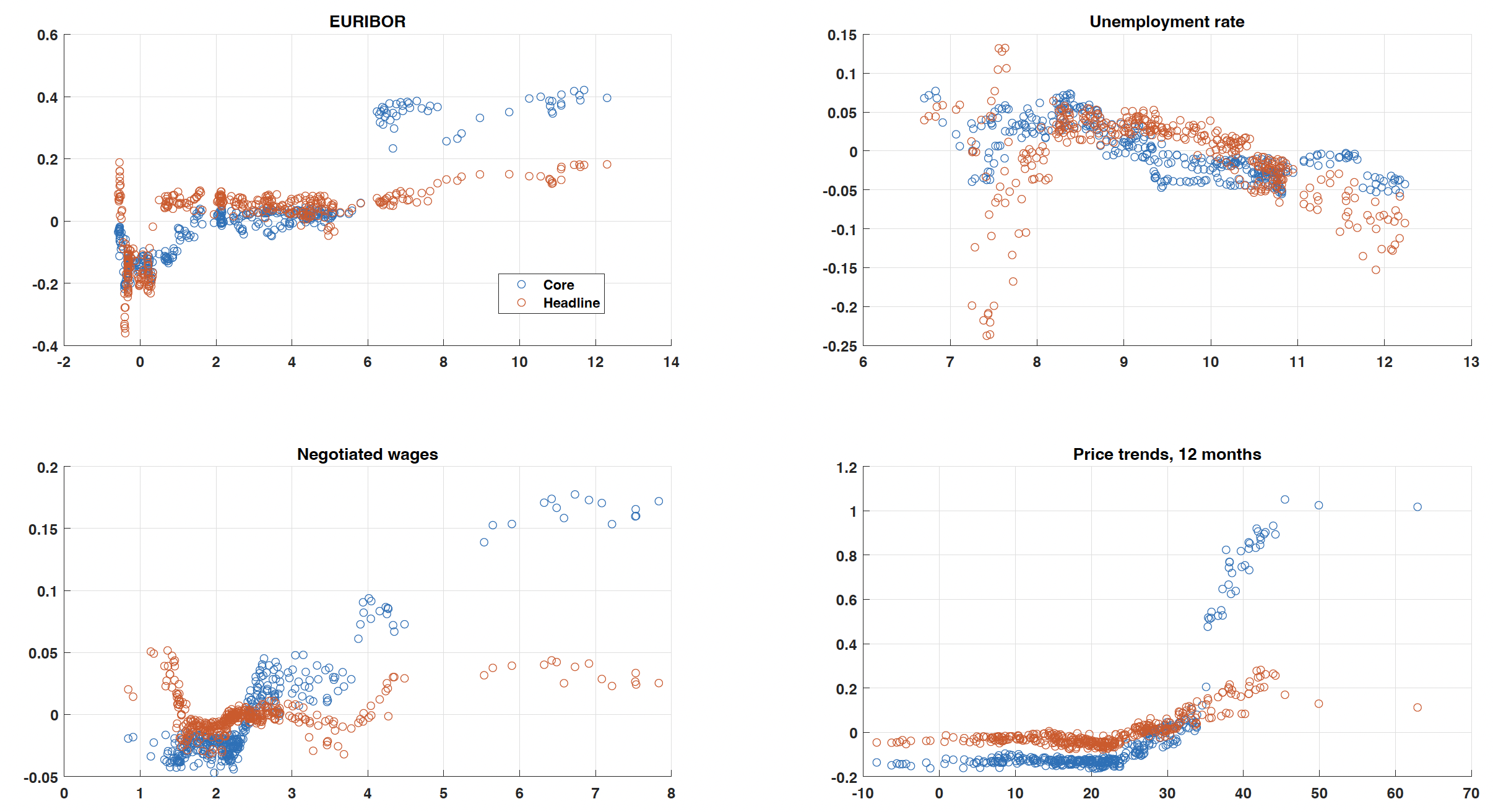
Such contributions are not meant to capture economic causality. They can, however, help both to identify the variables from which our model extracts the signal for the inflation outlook and to draw comparisons with other macroeconomic models. In addition, the way contributions of a specific variable evolve over the full sample may indicate the type of relationship between inflation and that variable, and help us spot potential non-linear patterns. Figure 1 shows the contributions to inflation of four variables in our set that turned out to be particularly relevant for headline and core inflation.
Figure 1 Contributions of different variables to headline and core inflation
Notes: Vertical axis: in-sample contribution to the deviation from the mean of the variable specified in the title of each panel for headline inflation (red) and core inflation (blue). The values are expressed in terms of percentage points. Horizontal axis: value of the variable specified in the title of each panel.
For three of these variables, the relationship with inflation seems roughly linear. The EURIBOR (the euro interbank offered rate) is often used as a proxy for the ECB’s monetary policy stance. Its relationship with inflation reflects the systematic reaction of monetary policy to inflation; it is essentially linear. The only non-linearity seems to relate to the effective lower bound of nominal interest rates. The chart showing the unemployment rate suggests the existence of a generally linear (Phillips curve-type) relationship, with a slight negative slope. And finally, the relationship between wages and inflation also appears roughly linear. However, for the measure of inflation expectations reported in the chart, i.e. 'price trends expected over the next 12 months’,
the relationship with headline and especially core inflation is clearly non-linear. Specifically, the chart suggests that, beyond a certain threshold in the share of survey respondents who expect higher inflation, inflation markedly accelerates.
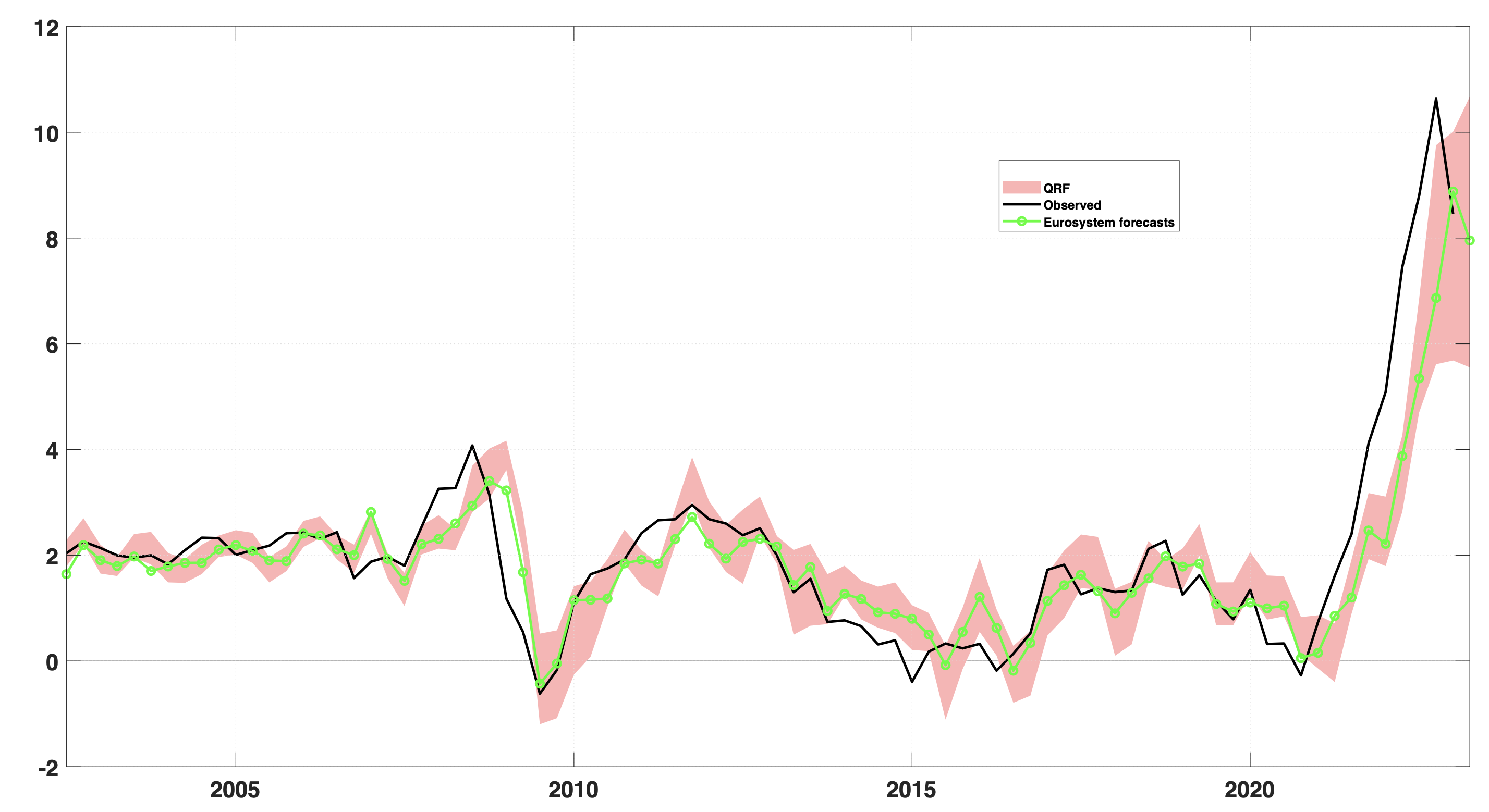
How do the predictions of the non-linear model compare with forecasts that incorporate expert judgement, namely those from the ECB Survey of Professional Forecasters (SPF) and the Eurosystem staff inflation projections? We find that the SPF forecasts one year ahead are more accurate than those from the non-linear model, while for shorter horizons the non-linear model is more accurate. Comparing the non-linear model with the Eurosystem staff projections, we find that the two sets of forecasts are very similar and display similar patterns of non-linearity. Figure 2 reports the density forecasts for headline inflation six months ahead from the non-linear model, together with the Eurosystem staff projections and observed inflation for the period 2002-22. The striking similarity, highlighted in the chart, also implies that both sets of forecasts exhibit a similar deviation from the forecasts of the linear model mentioned above. Given the vast prevalence of linear models in the Eurosystem forecasting toolbox observed in Darracq Pariès et al. (2021), this finding suggests that the so-called expert judgement component of the Eurosystem staff inflation forecasts may help embed mild non-linearity in the inflation projections.
Figure 2 Headline inflation and forecasts
Note: Black solid line: year-on-year growth rate of the HICP (headline inflation); red area: 16th to 84th quantiles of the density forecasts from the non-linear model (QRF), with a horizon of six months ahead, for the year-on-year growth rate of the HICP; green line with circles: Eurosystem inflation projections, with a horizon of six months ahead, for the year-on-year growth rate of the HICP.
Conclusions
A state-of the-art machine learning model, the quantile regression forest, is a valid addition to the Eurosystem projection toolbox. It is roughly comparable in accuracy to the linear models currently making up the bulk of the Eurosystem inflation forecasting toolbox. Accordingly, this new methodology should be seen as a complement to, rather than a substitute for, existing techniques. In addition, the assumption of linearity characterising most models in central banks’ toolboxes does not appear to be too wide of the mark. Our findings also show that the Eurosystem staff projections are in line with state-of-the-art econometric methodologies.
Authors’ note: This column first appeared as a Research Bulletin of the European Central Bank. The authors gratefully acknowledge the comments from Gareth Budden, Alexandra Buist, Michael Ehrmann, Alexander Popov, and Zoë Sprokel. The views expressed here are those of the author and do not necessarily represent the views of the European Central Bank or the Eurosystem.
References
Breiman, L (2001), “Random Forests”, Machine Learning 45: 5-32.
Cavallo, A, F Lippi and K Miyahara (2023), “Large Shocks Travel Fast”, NBER Working Paper No 31659.
Christiano, L J, M Eichenbaum and C L Evans (1999), “Monetary Policy Shocks: What Have We Learned and to What End?”, in J B Taylor and M Woodford (eds.), Handbook of Macroeconomics, Vol. 1, Chapter 2, pp. 65-148, Elsevier.
Clark, T E, F Huber, G Koop, M Marcellino and M Pfarrhofer (2023), “Tail Forecasting with Multivariate Bayesian Additive Regression Trees”, International Economic Review 64(3): 979-1022.
Costain, J, A Nakov and B Petit (2022), “Flattening of the Phillips Curve with State-Dependent Prices and Wages”, The Economic Journal 132(642): 546-581.
Darracq Pariès, M, A Notarpietro, J Kilponen, N Papadopoulou, S Zimic, P Aldama, G Langenus, L J Alvarez, M Lemoine and E Angelini (2021), “Review of Macroeconomic Modelling in the Eurosystem: Current Practices and Scope for Improvement”, Occasional Paper Series, No 267, ECB.
Giannone, D, M Lenza and L Reichlin (2019), “Money, Credit, Monetary Policy, and the Business Cycle in the Euro Area: What Has Changed Since the Crisis?”, International Journal of Central Banking 15(5): 137-173, December.
Goodhart, C (2023), “Should Central Banks abandon single point forecasts?”, VoxEU.org, 29 August.
Jarociński, M and P Karadi (2020), “Deconstructing Monetary Policy Surprises – The Role of Information Shocks”, American Economic Journal: Macroeconomics 12(2): 1-43, April.
Koester, G, E Lis, C Nickel, C Osbat and F Smets (2021), “Understanding Low Inflation in the Euro Area from 2013 to 2019: Cyclical and Structural Drivers”, ECB Occasional Paper Series No 280.
Lenza, M, I Moutachaker and J Paredes (2023), “Density Forecasts of Inflation: A Quantile Regression Forest Approach”, ECB Working Paper Series No 2830.
Medeiros, M C, G F Vasconcelos, A Veiga and E Zilberman (2021), “Forecasting Inflation in a Data-Rich Environment: The Benefits of Machine Learning Methods”, Journal of Business and Economic Statistics 39: 98-119.
Meinshausen, N (2006), “Quantile Regression Forests”, Journal of Machine Learning Research 7: 983-999.
Schnabel, I (2023), “The risks of stubborn inflation”, speech at the Euro50 Group conference on “New challenges for the Economic and Monetary Union in the post-crisis environment”.