Advancing science, technology, engineering and maths (STEM) education is a policy objective in many countries. But policies focused on increasing students’ maths skills tend to ignore the importance of comparative advantage in occupational choice. While skills-based comparative advantage has been used to explain college attendance (Willis and Rosen 1979), selection effects on wages (Heckman and Sedlacek 1985), and study choice (Kirkeboen et al. 2016), little is known about the underlying sources of differences in comparative advantage – or their malleability – across individuals. Understanding both the source and the malleability of comparative advantages is essential when considering policies that might be employed to increase the prevalence of STEM-trained workers.
We show that skills-based comparative advantage is transferred intergenerationally. Parents with a comparative advantage in maths (versus language) skills are significantly more likely to have children with a similar maths skill advantage (Hanushek et al. 2023). We also find that parents’ comparative skill advantage is not only a strong predictor of their own STEM choices, but also affects STEM choices of their children. Importantly, the intergenerational transmission of comparative maths skills is malleable through the education system.
The analysis builds on a unique data set that provides comparable measures of different domains of cognitive skills for parents and their children. The Intergenerational Transmission of Skills dataset (Jacobs et al. 2021) links Dutch survey data on parent skills in maths and language at around age 12–13 (collected in 1977, 1982, and 1989) to register data on their children’s skills in the same subjects elicited by similar tests at the same age between 2006 and 2019. In total, the combined dataset includes skills data for more than 25,000 parents and 40,000 of their children. The dataset also provides detailed information on grandparental education and social status as well as on test taking location, which can be used to control for the influence of extended family members on children’s outcomes (Adermon et al. 2021).
Our cognitive skill measures are based on the CITO test, a national high-stakes exam measuring school performance in maths and language (along with other subjects). The Dutch education system is an early stratifying system, where students are allocated to different tracks (low, middle, or high) after primary education (grade 6, at age 12) based on scores on the CITO test. We focus throughout on the ordinal properties of the maths and language assessments by analysing child and parent skills as percentile ranks in the overall skill distributions. This guards against concerns about assuming cardinal properties for standard assessments as found in most economic analyses that include test scores (see Bond and Lang 2013, Nielsen 2015).
The intergenerational skill data permit us to investigate the sources of comparative advantage. For this, we exploit within-family, between-subject variation in cognitive skills by relating differences in parents’ skills between maths and language to differences in maths and language skills of their children. All observed and unobserved influences of family, school, and neighbourhoods that do not differentially affect the two skill domains are eliminated in this within-family estimation.
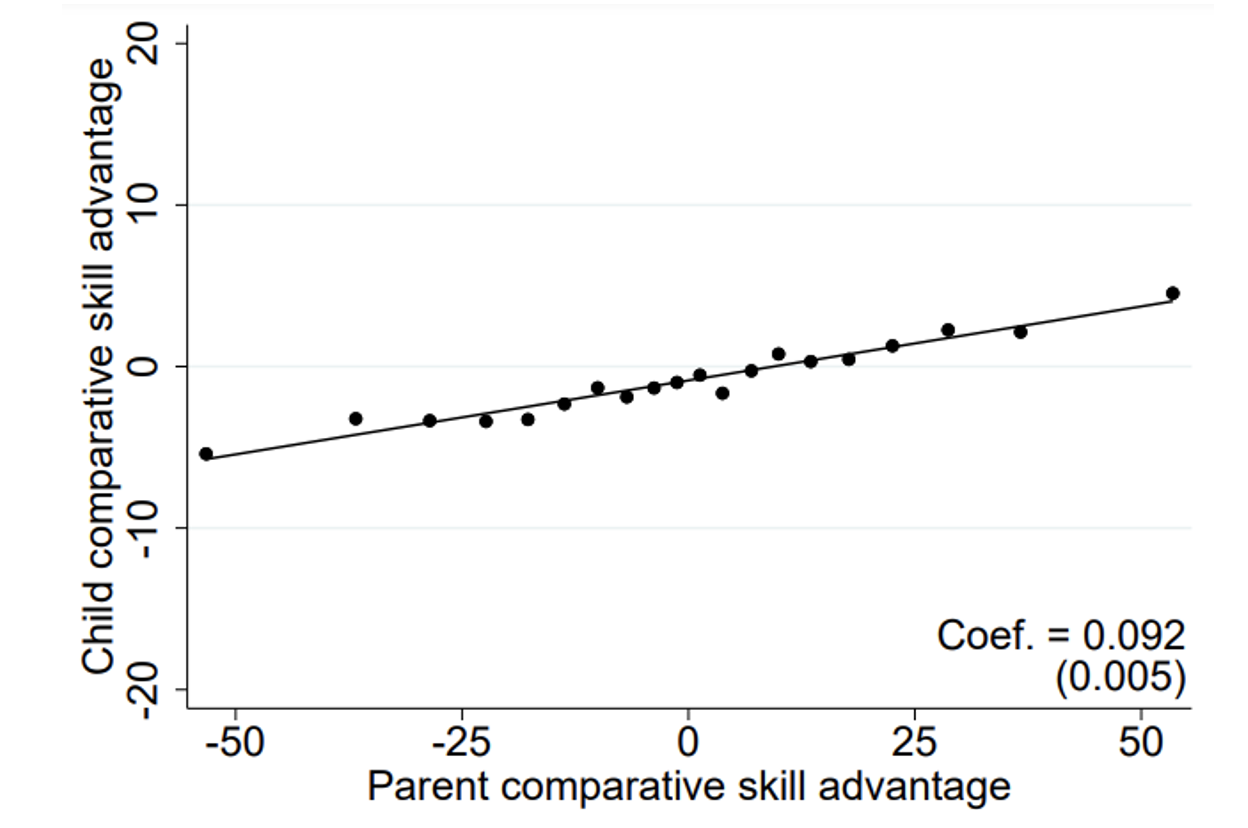
We find that parents with a comparative advantage in maths skills are significantly more likely to have children with a similar maths skill advantage, as can be seen in Figure 1. In terms of magnitude, a difference of 10 percentile ranks between skills in maths and language in the parent generation translates into around a one-rank difference in the child generation. The estimates are virtually unaffected by allowing for the possibility that various grandparental characteristics and regional factors affect maths and language skills differently. These results add to previous literature showing a strong intergenerational persistence between parents and children in income (Björklund and Jäntti 2011, Solon 1999), educational attainment (Björklund and Salvanes 2011, Schüle et al. 2021), and occupational status (Long and Ferrie 2013).
Interestingly, and in contrast to results from earlier literature (e.g. Black et al. 2005, Holmlund et al. 2011, Piopiunik 2014), the strength of the intergenerational transmission of comparative skill advantages does not vary by the gender match of parents and their children.
Figure 1 Intergenerational transmission of comparative skill advantages
Notes: The figure displays a binned scatterplot showing the strength of parent-child transmissions in comparative skill advantages. Comparative skill advantage is measured as the difference between the percentile ranks of maths and language test scores in the full sample of test takers. The best-fit line, the coefficient, and the standard error (clustered at the parent level) are calculated from bivariate regressions on the micro data.
To go deeper into the malleability of comparative skill advantage, we use a novel instrumental variable (IV) estimation exploiting differences between maths and language skills of the parents’ classroom peers to isolate variation in parents’ comparative skill advantage developed outside the family. In doing this, we look at the impact of parental comparative advantages that are related to the maths or language intensity of their educational experiences around the end of primary schooling (driven, for example, by subject-specific teacher quality). The IV analysis corroborates the results from the baseline estimation, showing a remarkably similar strength of the intergenerational transmission of comparative advantages. Thus, the comparative skill environment of parents’ early formal education significantly affects comparative skill advantages that carry over to future generations. This would not be the case if the observed skill transmission patterns reflected differences in innate ability alone, and implies that any policy that shifts focus from one skill domain to another not only affects the comparative skill advantage of the current students but also has a lasting impact on subsequent generations.
The IV analysis also has an important methodological aspect because estimation of difference models like those we employ are potentially subject to increased biases from measurement error. The IV approach deals with concerns about errors in our skill measures. It also addresses the possibility of bias from omitted subject-specific proclivities of families.
Finally, we return to how parents influence the long-run path of children. In particular, although academic and policy attention has focused on increasing the number of individuals entering STEM fields of study and occupations (e.g. UNESCO 2017), the role of families in influencing STEM choices has received little attention (Altonji et al. 2016). There are two key decision points in the Dutch education system that enter in ultimate STEM preparation. The first is the choice of concentration of courses in secondary school. The second, which is strongly affected by prior course choice, is the decision about field of study in post-secondary schooling.
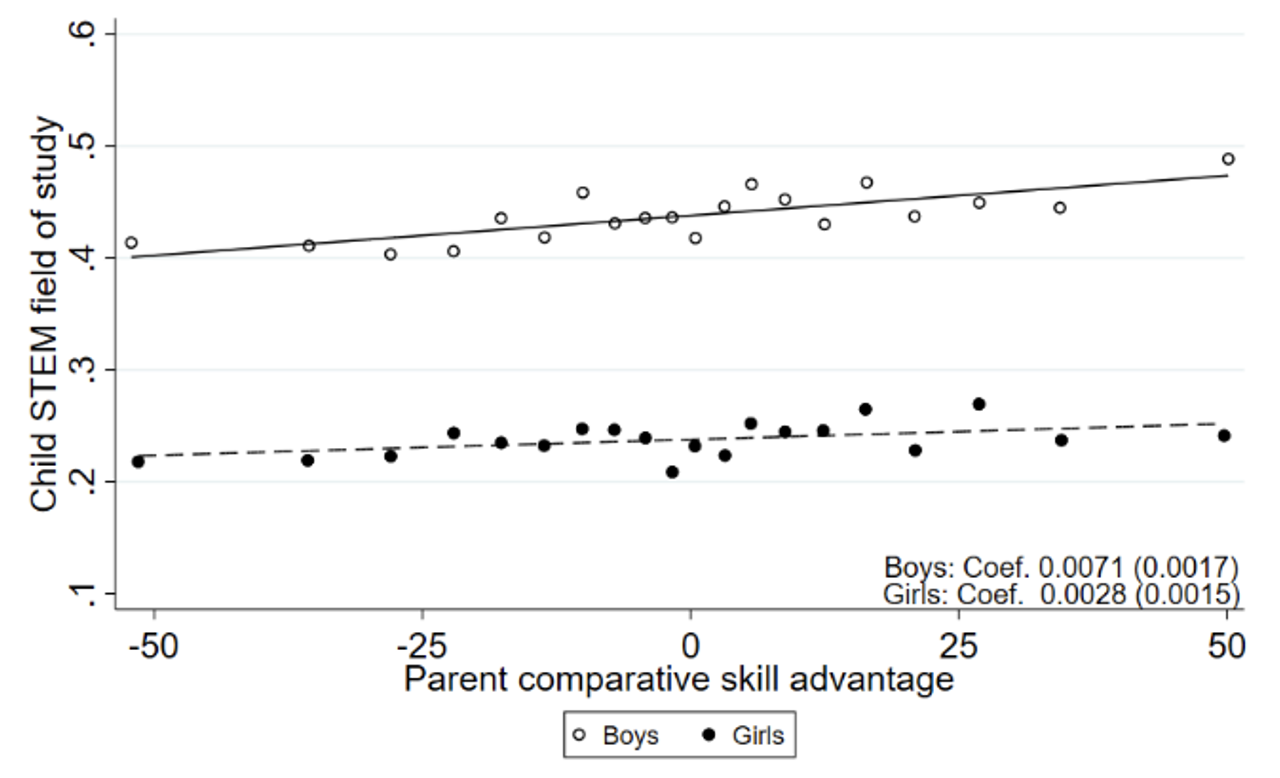
As can be seen from Figure 2, parents with a comparative advantage in maths (language) produce children who are more likely to opt for STEM (non-STEM) fields, just as would be suggested by a simple Roy model of occupational choice (Roy 1951). As mentioned above, parents influence the comparative skill advantages of both boys and girls similarly, leading to similar course patterns in secondary school (top panel). But ultimately, comparative skill advantages have somewhat less influence on girls’ choices of STEM field of study than on boys’ choices, independent of preparation (bottom panel). This potentially contributes to the frequently observed lower participation of girls in STEM occupations. Taken together, our results show that the intergenerational transmission of comparative advantage has important consequences for children’s educational pathways.
Figure 2 Parent comparative advantage and child STEM outcomes
Notes: The figure displays a binned scatterplot showing the strength of the association between parent comparative skill advantage and child STEM course choice in secondary school (top panel) and STEM field-of-study choice (bottom panel) by child gender.
Our results carry an important message regarding policies aimed at increasing the number of STEM-trained workers. The importance of skill-based comparative advantages in determining STEM choices, together with its malleability through environmental factors, suggest that any policy changing the relative cognitive skills of students today will also spillover to future generations, having a lasting impact on the sorting into STEM fields.
References
Altonji, J G, P Arcidiacono and A Maurel (2016), “The Analysis of Field Choice in College and Graduate School: Determinants and Wage Effects”, Handbook of the Economics of Education, vol. 5, Amsterdam: 305–396.
Adermon, A, M Lindahl and M Palme (2021), “Dynastic Human Capital, Inequality, and Intergenerational Mobility”, American Economic Review 111(5): 1523–1548.
Altonji, J G, P Arcidiacono and A Maurel (2016), “The Analysis of Field Choice in College and Graduate School: Determinants and Wage Effects”, Handbook of the Economics of Education, vol. 5, Amsterdam: 305–396.
Björklund, A and M Jäntti (2011), “Intergenerational Income Mobility and the Role of Family Background”, The Oxford Handbook of Economic Inequality, Oxford University Press.
Björklund, A and K G Salvanes (2011), “Education and family background: Mechanisms and policies”, Handbook of the Economics of Education, vol. 3, Amsterdam: 201–247.
Black, S E, P J Devereux and K G Salvanes (2005), “Why the apple doesn’t fall far: Understanding intergenerational transmission of human capital”, American Economic Review 95(1): 437–449.
Bond, T N and K Lang (2013), “The Evolution of the Black-White Test Score Gap in Grades K-3: The Fragility of Results”, Review of Economics and Statistics 95(5): 1468–1479.
Hanushek, E A, B Jacobs, G Schwerdt, R van der Velden, S Vermeulen, and S Wiederhold (2023), "Where Do STEM Graduates Stem From? The Intergenerational Transmission of Comparative Skill Advantages", NBER Working Paper No. 31186.
Heckman, J J and G Sedlacek (1985), “Heterogeneity, Aggregation, and Market Wage Functions: An Empirical Model of Self-Selection in the Labor Market”, Journal of Political Economy 93(6): 1077–1125.
Holmlund, H, M Lindahl and E Plug (2011), “The causal effect of parents’ schooling on children’s schooling: A comparison of estimation methods”, Journal of Economic Literature 49(3): 615–651.
Kirkeboen, L J, E Leuven and M Mogstad (2016), “Field of study, earnings, and self-selection”, Quarterly Journal of Economics 131(3): 1057–1111.
Long, J and J Ferrie (2013), “Intergenerational Occupational Mobility in Great Britain and the United States since 1850”, American Economic Review 103(4): 1109–37.
Nielsen, E R (2015), “The Income-Achievement Gap and Adult Outcome Inequality”, Finance and Economics Discussion Series 2015–041, Washington, DC: Federal Reserve Board.
Piopiunik, M (2014), “Intergenerational transmission of education and mediating channels: Evidence from a compulsory schooling reform in Germany”, Scandinavian Journal of Economics 116(3): 878–907.
Roy, A D (1951), “Some Thoughts on the Distribution of Earnings”, Oxford Economic Papers 3(2): 135–146.
Schüle, P, D Sachs, L Henkel, S Findeisen and M Dodin (2021), “New evidence on social mobility in Germany”, VoxEU.org, 24 December.
Solon, G (1999), “Intergenerational mobility in the labor market”, Handbook of Labor Economics, Amsterdam: 1761–1800.
UNESCO (2017), Cracking the code: Girls’ and women’s education in science, technology, engineering and mathematics (STEM), Paris: UN Educational, Scientific and Cultural Organization.
Willis, R J and S Rosen (1979), “Education and self-selection”, Journal of Political Economy 87(5): S65–S98.