Collaborations between researchers in economics have become significantly more important in recent decades. In 1996, multi-authored papers accounted for 50% of all articles published in economics. This number increased to over 75% in 2014 (Kuld and O’Hagan 2018, Ductor 2014). Through such collaborations, researchers generate spillovers not only for their direct collaboration partners, but also indirectly to other researchers connected to them within a complex network of collaborations. However, despite the increasing importance of collaborations in the scientific knowledge production process, existing research policies and funding agencies do not take spillovers in the co-authorship network into account.
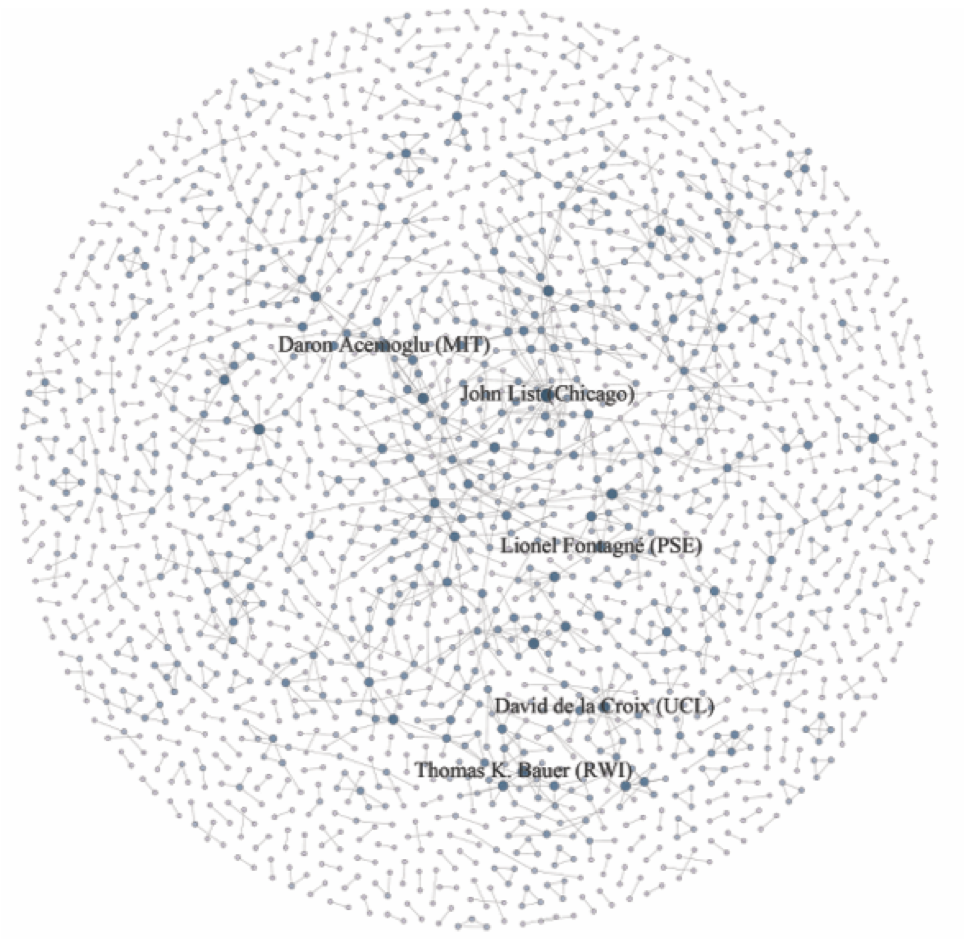
In a recent paper, we develop a novel model that allows us to rank researchers and evaluate research funding schemes by taking spillovers in the co-authorship network into account (Hsieh et al. 2018). In this model, spillovers manifest themselves through complementarities in the research efforts among collaborating researchers. We estimate this model using data for the network of scientific co-authorships among economists registered in the Research Papers in Economics Author Service (RePEc). An illustration of the co-authorship network from the RePEc data can be seen in Figure 1. The unobserved research effort levels are determined by the Nash equilibrium prediction of the model (Cabrales et al. 2011, Jackson and Wolinsky 1996), while the self-selection of researchers into different projects is determined by a matching process that takes into account both the researchers’ and projects’ characteristics (Chandrasekhar and Jackson 2012, Friel et al. 2016).
Figure 1 The collaboration network among authors in the RePEc database
Notes: Considers only co-authored projects, dropping projects with zero citations. A node’s size and shade indicate its degree (i.e., the number of co-authors). The names of the five authors with the largest degrees are indicated in the network. These are with decreasing order of degree: John List (University of Chicago), Daron Acemoglu (MIT), Thomas K Bauer (Leibniz Institute for Economic Research), Lionel Fontagné (Paris School of Economics), and David de la Croix (Université Catholique de Louvain).
Rankings
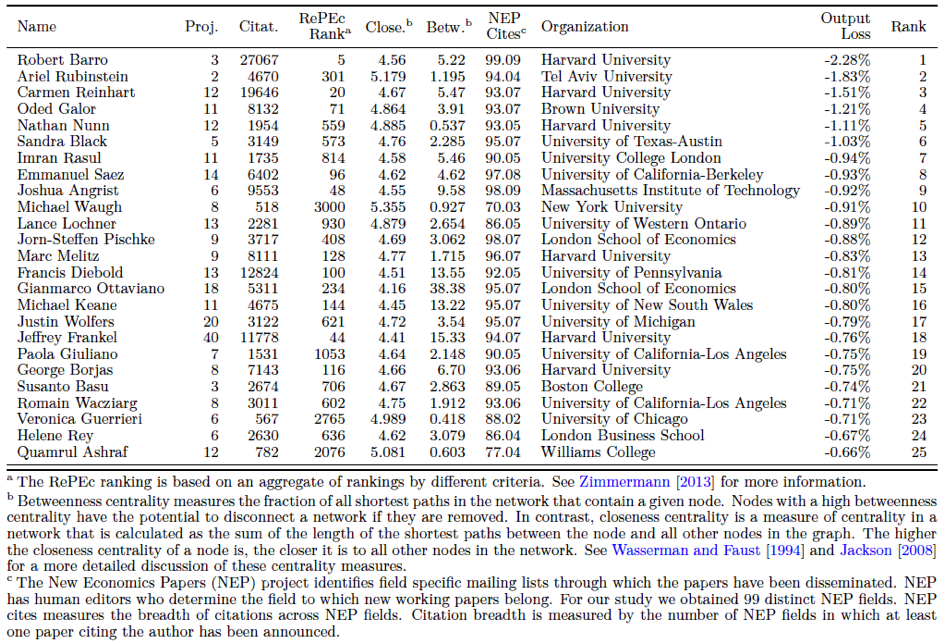
We then propose a novel ranking measure for economists and their departments. Our ranking quantifies the endogenous decline in total research output due to the removal of an economist from the co-authorship network (Ballester et al. 2006, König et al. 2018) and allows us to determine ‘key players’ (Zenou 2015), or ‘superstar’ economists (Azoulay et al. 2010, Waldinger 2010, 2012). Table 1 provides a ranking of the top 25 researchers based on the estimation results using a sample over the years 2010–2012. Taking into account endogenous effort choices of the authors and their interdependencies (research effort spillovers) across the co-authorship network, we find that the highest-ranked authors are not necessarily the ones with the largest number of citations, and that our ranking doesn’t coincide with other rankings used in the literature. This discrepancy is not surprising, however, as traditional rankings are not derived from economic microfoundations and typically do not consider the spillover effects generated in scientific knowledge production networks.
Table 1 Ranking of the top 25 researchers from the 2010–2012 sample
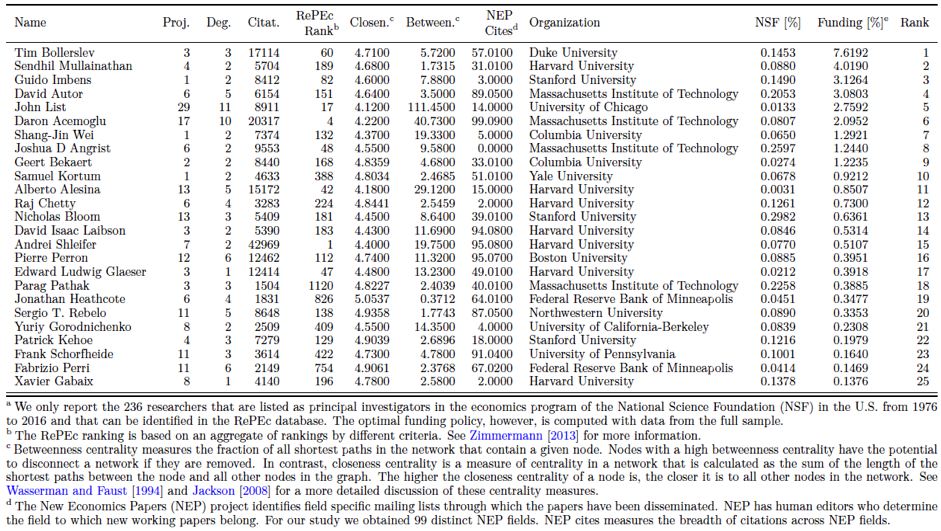
Our economic model further allows us to solve the optimal research funding problem of a planner whose aim is to maximise total research output by introducing research grants into the author’s payoff function (Stephan 2012, De Frajay 2016, König et al. 2018). Table 2 provides the optimal funding ranking for the top 25 researchers based on estimation results using the 2010–2012 sample period. We then aggregate researchers by their research institutions and departments and compute the optimal funding rank for these institutions/departments (Aghion et al. 2010). A comparison of our optimal funding policy with the research funding of the economics program of the National Science Foundation (NSF) indicates that there are significant differences, both at the individual and the institutional/departmental levels. In particular, we find that our optimal funding policy is significantly positively correlated with the number of co-authors (i.e. the degree in the co-authorship network) of an author. In contrast, the NSF awards turn out to be uncorrelated with the degree and they are positively but not significantly correlated with the optimal funding policy proposed in this study. This highlights the importance of the co-authorship network in determining optimal funding policy, in contrast to existing research funding programs such as the one by the NSF.
Table 2 The optimal research funding rank for the top 25 researchers in the 2010–2012 sample
Note that the optimal funding rankings (Table 2) deviate from the key player rankings (Table 1) because of the different objectives of these two counterfactual studies. While key player ranking identifies the authors that are already highly productive and exert large spillover effects on their co-authors, the optimal funding policy identifies the authors who can become key players by providing them with additional incentives through a merit-based funding scheme.
Policy implications
In this column we have proposed a novel model in which researchers seek to maximise the quality of their scientific output when being involved in multiple, possibly overlapping projects with co-authors. We show that, given an allocation of researchers to different projects, the Nash equilibrium can be completely characterised and used for inferring the empirically unobserved research effort levels. We bring our model to the data by analysing the network of co-authorship among economists registered in RePEc. Using the estimated model, we rank the authors and their departments according to their contributions to aggregate research output, and thus provide a novel ranking measure based on microeconomic foundations that identifies the key players in the network.
Moreover, we analyse research funding instruments for individual researchers as well as their departments. We show that, because current funding schemes do not take into account the availability of co-authorship network data, they are ill-designed to take advantage of the spillover effects generated in scientific knowledge production networks. Indeed, the optimal funding policy outcomes deviate substantially from the ones currently implemented by policymakers because we incorporate the co-authorship (network) externality in the policymaker’s objective function.
Editor’s note: The views expressed here are those of individual authors and do not necessarily reflect official positions of the Federal Reserve Bank of St. Louis, The Federal Reserve System, or the Board of Governors.
References
Aghion, P, M Dewatripont, C Hoxby, A Mas-Colell and A Sapir (2010), “The governance and performance of universities: Evidence from Europe and the US,” Economic Policy 25(61): 7–59.
Azoulay, P, J G Zivin and J Wang (2010), “Superstar extinction,” Quarterly Journal of Economics 125(2): 549–589.
Ballester, C, A Calvó-Armengol and Y Zenou (2006), “Who’s who in networks— Wanted: The key player,” Econometrica 74(5): 1403–1417.
Cabrales, A, A Calvó-Armengol and Y Zenou (2011), “Social interactions and spillovers,” Games and Economic Behavior 72(2): 339–360.
Chandrasekhar, A and M Jackson (2012), “Tractable and consistent random graph models,” available at SSRN 2150428.
Ductor, L (2014), “Does co-authorship lead to higher academic productivity?” Oxford Bulletin of Economics and Statistics 77(3): 385–407.
De Frajay, G (2016), “Optimal public funding for research: A theoretical analysis,” RAND Journal of Economics 47(3): 498–528.
Friel, N, R Rastelli, J Wyse and A E Raftery (2016), “Interlocking directorates in Irish companies using a latent space model for bipartite networks,” Proceedings of the National Academy of Sciences 113(24): 6629–6634.
Graham, B S (2015), “Methods of identification in social networks,” Annual Review of Economics 7(1): 465–485.
Graham, B S (2017), “An econometric model of network formation with degree heterogeneity,” Econometrica 85(4): 1033–1063.
Hess, A M and F T Rothaermel (2011), “When are assets complementary? Star scientists, strategic alliances, and innovation in the pharmaceutical industry,” Strategic Management Journal 32(8): 895–909.
Hollis, A (2001), “Co-authorship and the output of academic economists,” Labour Economics 8(4): 503–530.
Hsie, C S, M D König, X Liu and C Zimmermann (2018), “Superstar economists: Co-authorship networks and research output,” CEPR Discussion Paper 13239.
Jackson, M O and A Wolinsky (1996), “A strategic model of social and economic networks,” Journal of Economic Theory 71(1): 44–74.
Jackson, M (2008), Social and Economic Networks, Princeton University Press.
König, M D, X Liu and Y Zenou (2018), “R&D networks: Theory, empirics and policy implications,” Review of Economics and Statistics, forthcoming.
Kuld, L and J O’Hagan (2018), “Rise of multi-authored papers in economics: Demise of the ‘lone star’ and why?” Scientometrics 114(3): 1207–1225.
Liu, X, E Patacchini, Y Zenou and L Lee (2011), “Criminal networks: Who is the key player?” Stockholm University, Research Papers in Economics.
Stephan, P E (2012), How economics shapes science, Harvard University Press.
Waldinger, F (2010), “Quality matters: The expulsion of professors and the consequences for PhD student outcomes in Nazi Germany,” Journal of Political Economy 118(4): 787–831.
Waldinger, F (2012), “Peer effects in science: evidence from the dismissal of scientists in Nazi Germany,” Review of Economic Studies 79(2): 838–861.
Wasserman, S and K Faust (1994), Social Network Analysis: Methods and Applications, Cambridge University Press.
Zenou, Y (2015), “Key players,” Y Bramoulle, B Rogers and A Galeotti (eds), Oxford Handbook on the Economics of Networks, Oxford University Press.
Zimmermann, C (2013), “Academic rankings with RePEc,” Econometrics 1(3): 249–280.