Few economic concepts can match the empirical success of the gravity equation as one of the most commonly applied models in international economics (see Anderson 2011 and Head and Mayer 2014 for recent surveys). Analogous to Newton’s universal law of gravitation, the gravity equation for trade predicts that the value of bilateral trade is positively related to the economic masses of the considered regions, and inversely related to the (geographic) distance between these regions. Its empirical success means that the gravity model is not only applied in international trade, but has also become a standard tool to explain and predict the volume of intra-national trade between different regions or cities within countries (for a recent example see Allen and Arkolakis 2014; for a recent survey see Redding and Rossi-Hansberg 2017).
The backbone of the empirical gravity equation is the assumption that the distribution of industries across space is exogenous. This assumption is shared by most international trade models. While the industry margin, for obvious reasons, cannot be analysed within single-sector models (Head and Mayer 2014), the latest generation of multi-sector models typically assumes that all industries can be found in all locations (Costinot and Rodríguez-Clare 2014).
Based on trade between cities in Japan, we argue that the location of industries is endogenous (Mori and Wrona 2018), and that it roughly follows Christaller’s (1933) hierarchy principle for industries. This states that all industries that are present in a city of a given size are expected to be also present in all cities of equal or larger size (Mori et al. 2008, Mori and Smith 2011, Hsu 2012).
Central places and the pattern of inter-city trade
To characterise the pattern of inter-city trade when larger cities not only are larger in scale but also larger in scope (in terms of their industrial diversity), we use the new economic geography model of Fujita et al. (1999), who were among the first to formalise Christaller’s (1933) central place theory. In their model, agglomeration forces shape a hierarchical city system, in which most industries cluster in large, centrally located cities (so-called central places). These central places serve remote smaller cities with all the goods that these cities cannot produce, because the appropriate industries do not exist in these locations. Industry location thereby follows Christaller’s (1933) hierarchy principle. This states that industries with low trade costs optimally cluster in large, centrally located cities, while firms in industries with high trade costs choose locations close to their customers, and therefore can be found almost everywhere.
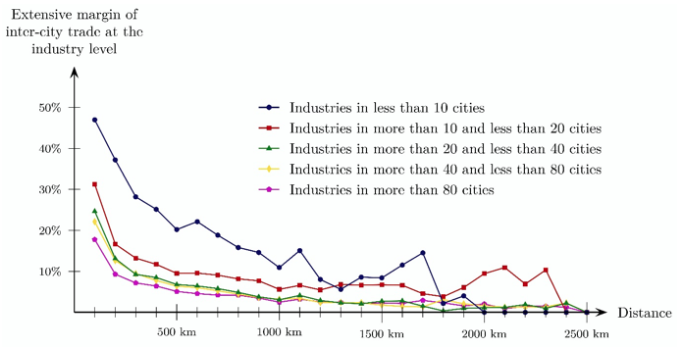
Different industries have differing trade costs, and so industry location is based on these trade cost differences. This has a direct effect on the pattern of inter-city trade, which we highlight in Figure 1. We classify industries according to the number of cities in which they can be found, and show the probability of serving a partner city declines with the distance to that partner city.
Figure 1 Export probabilities over varying distances by industry category in Japan
Source: Mori and Wrona (2018)
A comparison across industry categories shows that firms in industries that are only present in a limited number of cities are generally more likely to export to other cities in their hinterland than firms in industries that can essentially be found everywhere. Central places both have more industries and, in particular, more industries whose firms are more likely to export to other cities in their hinterland. So we would expect the aggregate exports of central places to their hinterlands to be larger than predicted by the standard gravity model for aggregate trade, because the standard model typically ignores (endogenous) differences in industrial diversity across cities.
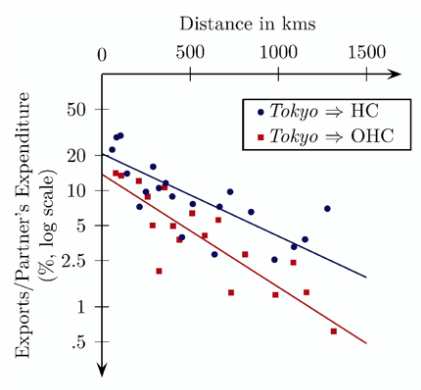
In Figure 2 we capture the spirit of the standard gravity model by normalising the exports from Japan’s most 'central' city (Tokyo) by the size of the respective destination city, allowing the normalised trade flows to differ by the bilateral distance to the destination city.
Figure 2 Tokyo’s exports to its own hinterland, and to the hinterlands of other central places
Source: Mori and Wrona (2018).
Note: Binned scatter plot. All destination cities fall into one of 20 distance bins, used to avoid clutter.
As we would expect, there is a strong trade-reducing effect of distance on the (normalised) volume of bilateral trade. In addition to the trade-reducing effect of distance, we also find that there is a level effect, when comparing Tokyo’s exports to cities in its hinterland (blue, abbreviated to HC) to exports of Tokyo to cities which we classify as hinterland cities of other central places (red, abbreviated to OHC) such as Osaka. Accounting not only for exports from Tokyo but also for exports originating from other central places that we can identify in our data, we find that aggregate exports from central places to their respective hinterlands exceed the export volume between comparable city pairs (conditional on gravity forces) by a factor of 2:5.
Disaggregation and decomposition of inter-city trade
To provide further empirical evidence that the upward bias in the exports of central places to their respective hinterlands is an artefact of an aggregation process that does not take into account Christaller’s (1933) hierarchy principle for industries, we repeat our analysis at a much more disaggregated level (roughly 200 industries). Fujita et al. (1999) showed that gravity is expected to hold at the industry level and so, given that the specific industry is present in the respective exporting city, we are not surprised to find that the upward bias in central places’ exports is much smaller, and often not statistically different from zero.
Following Hillberry and Hummels (2008), we could exploit the full potential of our micro-level trade data on intra-national shipments in Japan to decompose the upward bias in the exports of central places to their respective hinterlands. Being able to distinguish between the number of shipping industries, the average number of shipments per industry, the average price per shipment, and the average quantity per shipment, we find that the extensive industry margin (the number of shipping industries) is by far the most important driver behind the upward bias in central places’ exports. The extensive industry margin accounts for 42.1% to 65.7% of the upward bias in aggregate gravity estimations, whereas the number of shipments per industry hardly contributes at all (2.1% to 10.8%). In line with the central place model of Fujita et al. (1999), we find that large cities export more to cities in their hinterland because they serve these markets across a wider range of industries, and not because they are generally sending out more shipments (per industry).
Conclusion
Unlike data on international trade, which is collected and reported in great detail by customs authorities around the world, survey data on trade between regions within countries is typically more aggregated, and often is used to predict the demand for, as well as the returns to, public infrastructure investments. Due to the coarseness of the intra-national trade data, gravity estimations based on aggregate trade flows are likely to suffer from some form of aggregation bias that, a priori, would be unknown. We argue that the exports from large, centrally located cities (central places) to their nearby hinterland are systematically under-predicted by aggregate gravity estimations, because they ignore Christaller’s (1933) hierarchy principle for industries.
Rather than being genuinely better in exporting, we find that central places’ extraordinary export performance can be explained through the systematic self-selection of firms from export-oriented industries into large home markets. To avoid the aggregation bias that results from adding up industry-level trade flows across a set of hierarchically distributed industries, we suggest relying on theory-consistent gravity estimation at the industry-level.
References
Allen, T and C Arkolakis (2014), "Trade and the Topography of the Spatial Economy", The Quarterly Journal of Economics 129(3): 1085–1140.
Anderson, J E (2011), "The Gravity Model", Annual Review of Economics 3: 133–60.
Christaller, W (1933), Die zentralen Orte in Süddeutschland, translated by C W Baskin (1966) as Central Places in Southern Germany, Prentice-Hall.
Costinot, A and A Rodríguez-Clare (2014), "Chapter 4 - Trade Theory with Numbers: Quantifying the Consequences of Globalization", in K R E Helpman and G Gopinath (eds) Handbook of International Economics, volume 4, Elsevier: 197–261.
Fujita, M, P Krugman, and T Mori (1999), "On the Evolution of Hierarchical Urban Systems", European Economic Review 43: 209–251.
Head, K and T Mayer (2014), "Chapter 3 - Gravity Equations: Workhorse, Toolkit, and Cookbook", in K R E Helpman and G Gopinath (eds) Handbook of International Economics, volume 4, Elsevier: 131–95.
Hillberry, R and D Hummels (2008), "Trade Responses to Geographic Frictions: A Decomposition Using Micro-data", European Economic Review 52: 527–50.
Hsu, W (2012), "Central Place Theory and City Size Distribution", Economic Journal 122: 903–32.
Mori, T, K Nishikimi, and T E Smith (2008), "The Number-Average Size Rule: A New Empirical Relationship between Industrial Location and City Size", Journal of Regional Science 48: 165–211.
Mori, T and T E Smith (2011), "An Industrial Agglomeration Approach to Central Place and City Size Regularities", Journal of Regional Science 51: 694–731.
Mori, T and J Wrona (2018), "Inter-city Trade", RIETI discussion paper 18-E-067.
Redding, S J and E Rossi-Hansberg (2017), "Quantitative Spatial Economics", Annual Review of Economics 9: 21-58.