In the past 50 years or so, the gap between average living standards in the poorest countries of the world and those in the richest countries has grown markedly. This unwelcome change is contrary to the proposition that less advanced economies ought to be able to catch up to more advanced economies through capital accumulation and technology transfer. Although the proposition wasn’t new, Abramowitz’s (1986) and Baumol’s (1986) examinations of its veracity as a negative correlation between initial per capita income levels and subsequent growth in per capita income, initiated a vast literature testing the so-called convergence hypothesis.1 Following Barro and Sala-i-Martin (1990), the catch-up approach to the convergence hypothesis became known as β-convergence.2
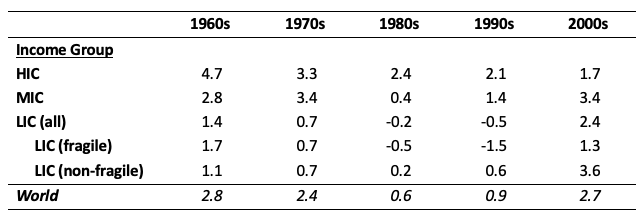
Table 1 provides some insight into what has driven the widening gap between the poorest countries and the richest countries. It shows decadal average per capita GDP growth rates for low, upper-middle, and high-income countries (LICs, MICs, and HICs respectively) over the 50-year period from 1960 to 2010.
Table 1 Decadal average per capita GDP growth (%) by income
Notes: This table is an abridged version of Table 2 in Johnson and Papageorgiou (2018) where data sources and other details are given. There are 29 HICs, 68 MICs, and 51 LICs. Appendix Table A.1 in Johnson and Papageorgiou (2018) lists the countries in each group.
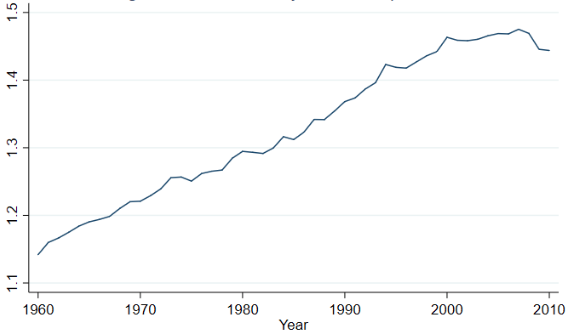
Despite the slowdown in their average growth rates over this period, the HICs have typically grown more quickly than the MICs, which in turn have grown more quickly than the LICs. These differences are the exact opposite of the pattern required for catching up to be observed, and so it is hardly a surprise that the dispersion of per capita GDP across countries has grown markedly since 1960. This growth is documented in Figure 1, which plots the standard deviation of the cross-country distribution of GDP per capita for a constant group of countries from 1960 to 2010 and shows that, apart from a small decline in the very late 2000s, the dispersion has risen steadily since 1960.
In addition to lagging that of the HICs and MICs, the growth experience of the poorest countries from 1960 to 2010 has been heterogeneous, both across countries and over time. Table 1 shows that the LICs experienced a continuous decline in growth rates in every decade from the 1960s to the 1990s, with negative growth rates in the 1980s and 1990s, before the surprising and unprecedented resurgence of growth in the 2000s. The MICs saw a similar resurgence in the 2000s although their slowing in the 1980s did not produce the negative growth rates experienced in the LICs.
Table 1 also makes the distinction between what are commonly called fragile and non-fragile LICs. Fragile states are those facing political frailty, characterised by weak institutional capacity, poor governance, corruption, and conflict. This distinction illuminates the marked differences in the growth experiences of the fragile LICs and the non-fragile of LICs, most notably in the 1990s and 2000s when the annual average growth rates differ by over 2 percentage points. That is, while there is a lot of optimism over the most recent growth acceleration in LICs, aggregating their experience masks the fact that only about half of the LICs are contributing to the resurgence while the rest are stagnant.
Coupled with the steady slowing of growth in the HICs, the resurgence in growth in the MICs and the non-fragile LICs has been strong enough to produce the slight decline in the dispersion of per capita GDP across countries beginning in the very late 2000s, evident in Figure 1. Responding to Johnson and Papageorgiou (2018), Patel et al. (2018) show that these events are sufficient to yield a small but statistically significant negative correlation between growth rates and initial income over, for example, the 1995 to 2010 period. This finding of weak β-convergence over a very short time period that contains important high and medium-frequency influences on GDP (e.g. the dot com bubble and its collapse and then the largest global economic slowdown since the 1930s and its immediate aftermath) leads them to claim that convergence is occurring.
As has been known for some time, the β-convergence testing approach is flawed and so the negative correlation observed over the 1995 to 2010 period does not imply that convergence is actually occurring. In statistical parlance, β-convergence tests can have low power against non-convergent alternatives. This means that such a test can yield a negative correlation even if convergence, which is correctly understood as the absence of a role for initial conditions in determining countries’ long-run per capita income levels, is not occurring. One way to think about this flaw in the β-convergence approach is that initial income doesn’t fully describe a country’s initial conditions as there are other important factors that influence growth going forward.
Figure 1 Cross-country income dispersion
Source: Figure 6 in Johnson and Papageorgiou (2018) where data sources and other details are given.
Notes: Convergence expressed as the decline in the dispersion of per capita GDP across countries is known as σ-convergence. As Barro and Sala-i-Martin (1990) show, β-convergence is necessary but not sufficient for σ-convergence so the absence of β-convergence for the 1960-2010 period displayed in Table 1 implies the absence of σ-convergence evident in Figure 1.
An economically interesting non-convergent alternative which admits the possibility that initial conditions can influence long-run per capita income levels is that of club convergence. Club convergence occurs when the growth process has more than one stable steady state, as can happen when there is a feedback loop from income to some other state variable. In such cases, economies converge to the steady state associated with the basin of attraction in which they begin. A country's long-run per capita income will then depend on its initial conditions as measured by the state variables determining its basin of attraction. Countries having similar initial conditions will converge locally and form a convergence club but global differences in per capita incomes will persist indefinitely. If there is just a single, stable steady state, initial conditions will be irrelevant for long-run per capita income levels and countries will exhibit catch-up or β-convergence as they gravitate towards it.
Many researchers, including us, have applied a wide range of empirical approaches in attempts to systematically identify convergence clubs. These approaches include the use of clustering algorithms in both the cross-section and time series contexts as well as projections of the cross-country distribution of per capita income based on its past evolution. Our reading of this literature (Johnson and Papageorgiou 2018) is that, once the alternative hypothesis of club convergence is explicitly considered, there is strong evidence contrary to the view that initial conditions do not matter for long-run outcomes. Instead, the data favour the view that initial conditions do matter and that the cross-country distribution of per capita income exhibits characteristics consistent with the existence of two or more convergence clubs.3 For this reason, the recent optimism in favour of rapid and sustainable convergence seems unfounded. Moreover, the growth in the dispersion of per capita GDP across countries since 1960 documented in Figure 1 suggests that the gaps between the mean levels of per capita GDP across the convergence clubs are increasing.
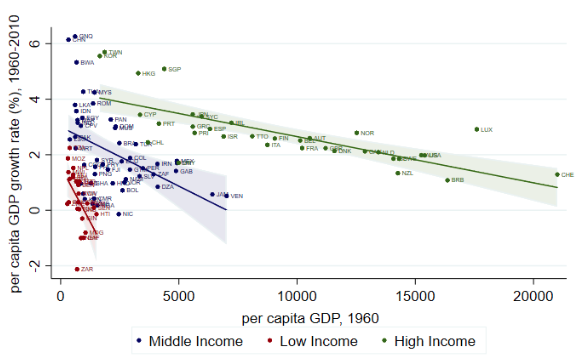
This tendency to local but not global convergence is illustrated in Figure 2 which plots the growth rate over 1960–2010 against the 1960 level of real per capita GDP for all of the HICs, MICs, and LICs, with counties in each group being shown in different colours. The negative correlation between initial income per capita and its subsequent growth indicative of catching up is evident within each of these three groups of countries even though it isn’t seen for the countries taken as a single group.
Figure 2 Growth against initial income
Source: Figure 4 in Johnson and Papageorgiou (2018), where data sources and other details are given.
The distinction between one single stable steady state and multiple stable steady states has important policy implications because, in the former case, small-scale policy interventions can be helpful to the extent that they hasten the transition of the poor countries to inevitable prosperity. However, if there are multiple stable steady states, then large-scale policy interventions may be required to push poor economies from one basin of attraction to another. In such a world, small scale policy interventions that fail to push countries into a different basin of attraction will eventually be undone as economies fall back to the steady state associated with the basin of attraction in which they lie. A multiplicity of steady states can lead to the sorts of poverty traps discussed by Collier (2007) or the hypothesised middle-income trap studied by Eichengreen et al. (2014). The fragile LICs are likely in such a poverty trap and so need a large-scale policy intervention (i.e. a change that removes their fragility) if they are to move to a steady state with higher per capita income.
The recent wave of growth in many LICs and emerging markets has led to many analysts to claim, prematurely in our view, success with slogans such as “lions on the move’ (McKinsey Global Institute 2010) or like Patel et al. (2018), to assert that “there has been unconditional convergence.” However, with the exception of a few countries in Asia which exhibited transformational growth, most of the economic achievements in developing economies have been the result of removing inefficiencies which are merely one-off level effects. While these effects are not unimportant and are necessary in the process of development, they do not imply ongoing economic growth. Moreover, we fear that the obstacles that Patel et al. (2018) cite in their conclusion, as well as the political fragility of many LICs, may undo what progress has recently occurred and cause many LICs to languish in a low-per-capita-income steady state.
References
Abramovitz, M (1986), “Catching Up, Forging Ahead, and Falling Behind,” Journal of Economic History 46(2): 385-406.
Barro, R J and X Sala-i-Martin, (1990), "Economic Growth and Convergence Across the United States." NBER Working Paper 3419
Baumol, W J (1986), “Productivity Growth, Convergence, and Welfare, What the Long-Run Data Show,” American Economic Review 76(5): 1072-1085.
Collier, P, (2007), The Bottom Billion: Why the Poorest Countries Are Failing and What Can Be Done About It. Oxford UK: Oxford University Press.
Dowrick, S and J B DeLong. (2003), “Globalization and Convergence”, in M D Bordo, A M Taylor and J G Williamson (eds), Globalization in Historical Perspective, NBER Conference Report series, University of Chicago Press.
Durlauf, S N and P A Johnson (1995), “Multiple Regimes and Cross-Country Growth Behavior,” Journal of Applied Econometrics 10(4): 365-284.
Durlauf, S N, P A Johnson, and J R W Temple. (2005), “Growth Econometrics,” in P Aghion and S N Durlauf (Eds.), Handbook of Economic Growth, North-Holland, 555-677.
Eichengreen, B, D Park and K Shin (2014), “Growth slowdowns redux”. Japan and the World Economy 32: 65-84.
Galor, O (2011), Unified Growth Theory, Princeton University Press.
Johnson, P, and C Papageorgiou (2018), “What Remains of Cross-Country Convergence?”, Journal of Economic Literature, forthcoming.
McKinsey Global Institute, (2010), Lions On the Move: The Progress and Potential of African Economies. McKinsey & Company.
Patel, D, J Sandefur and A Subramanian (2018), “Everything you know about cross-country convergence is (now) wrong”, PIIE Realtime Economic Issues Watch, 15 October.
Endnotes
[1] For surveys of this literature see, among others, Durlauf et al. (2005), and Johnson and Papageorgiou (2018).
[2] There are two variants of β-convergence: the absolute (or unconditional) variant that considers the correlation between initial per capita income levels and subsequent growth in per capita income and the conditional variant which considers the correlation after conditioning on variables thought to determine the steady state value of output per capita such as rates of physical and human capital accumulation and population growth. We are in agreement with Dowrick and DeLong’s (2003) criticism of the latter variant as, in effect, begging the convergence question and so consider only absolute β-convergence.
[3] Importantly, as Durlauf and Johnson (1995) point out, with the finite spans of data that are available, it is impossible to unequivocally distinguish between convergence clubs and countries transitioning through different stages of development before reaching a common steady state as implied by the unified growth theory of Galor (2011).