Without regular hard and soft data releases, traditional nowcasting models as those put forward by Giannone et al. (2008) and Stock and Watson (2002, 2012) become considerably constrained. These models may still be employed, although with little flexibility beyond scenario analysis and comparative exercises using past conflicts as empirical counterparties. Without any readings on consumption, investment, and production aggregates or their micro survey-based estimates, assessing the scale and speed of changes in the Ukrainian economy transformed from a well-tuned multistage process into a creative exploration of new machine learning (ML) variable selection and estimation algorithms.
The first necessary step in this context is replacing hard and soft data with alternative measures expected to correlate with the variable(s) of interest, in this case, Gross Domestic Product. This implies moving further back in the data creation value chain and finding appropriate alternative inputs and models, the outputs of which correlate well with GDP. In Constantinescu et al. (2022, 2023a), leveraging the less-than-perfect correlation among unconventional data sources, we present the preliminary results of forecasting annual regional GDP using night lights, social media activity, and Google search volumes. In this framework of low time frequency and intermediate geographic resolution, these data are useful to estimate the initial regional impact of the invasion using an otherwise standard bridge equation.
Partial least squares and variable selection
At the core of most big data nowcasting applications one may find algorithms estimating a small number of potential latent factors (with a dynamic structure) driving a large number of observed explanatory variables. Principal components (PCs) and maximum likelihood are currently the most widely employed estimation strategies of nowcasting models.
This estimation step may be improved by introducing a supervised machine learning algorithm as opposed to using principal component regressions, which is an unsupervised method. In partial least squares (also called ‘projection to latent structures’ in the chemometrics and genomics literature), the structural assumption is that a few latent factors drive both the Google Trends vectors and the univariate GDP observations (Wold et al. 1984, 2006, Helland 1990, Stoica and Söderström 1998). Naturally, the number of latent factors is strictly less than the number of Google Trends vectors. The objective of the algorithm is to recover both the latent factors as well as the loadings of both the explanatory and dependent variables on the factors via repeated partial regressions of GDP observations on the vectors of explanatory variables, ordered according to the covariance between them.
Why is variable selection needed in a partial least squares regression? Chun and Keleş (2010) indicate challenges to asymptotic consistency of the partial least squares estimator in contexts with many explanatory variables and relatively few observations, with a fixed number of relevant and an increasing number of irrelevant variables, a feature of our dataset comprised exclusively of Google Trends. The intuition for the lack of asymptotic consistency comes from the ridge-like nature of the partial least squares algorithm. Given that partial least squares latent factors load on all available variables, a larger fraction of irrelevant variables weakens the ability of the algorithm to identify the true factor directions.
Variable selection, also known as feature selection, is a step in the process of building predictive machine learning models particularly useful for small sample sizes or when model performance may be negatively impacted by possibly noisy inputs. It offers a means to improve model accuracy, reduce complexity, and enhance interpretability. Sparsity is achieved via variable selection in a multitude of ways, depending on the joint specificities of data sample and the machine learning model. Tsamardinos and Aliferis (2003) highlight the close connection between variable selection, model structure, and the evaluation metric in building predictive models.
Several methods are considered in the pre-selection stage, ranging from filter to wrapper and embedded feature selection methods. Chun and Keleş (2010) sparse partial least squares and a genetic algorithm are also presented.
Results
Target variables are deflated quarterly changes in aggregate GDP. The initial estimation timeframe is 2012 to 2021, reduced to 2013 to 2021 once appropriate lags are accounted for. The explanatory variables are a large number of Google Trends selected on the basis of prior studies and observed local preferences.
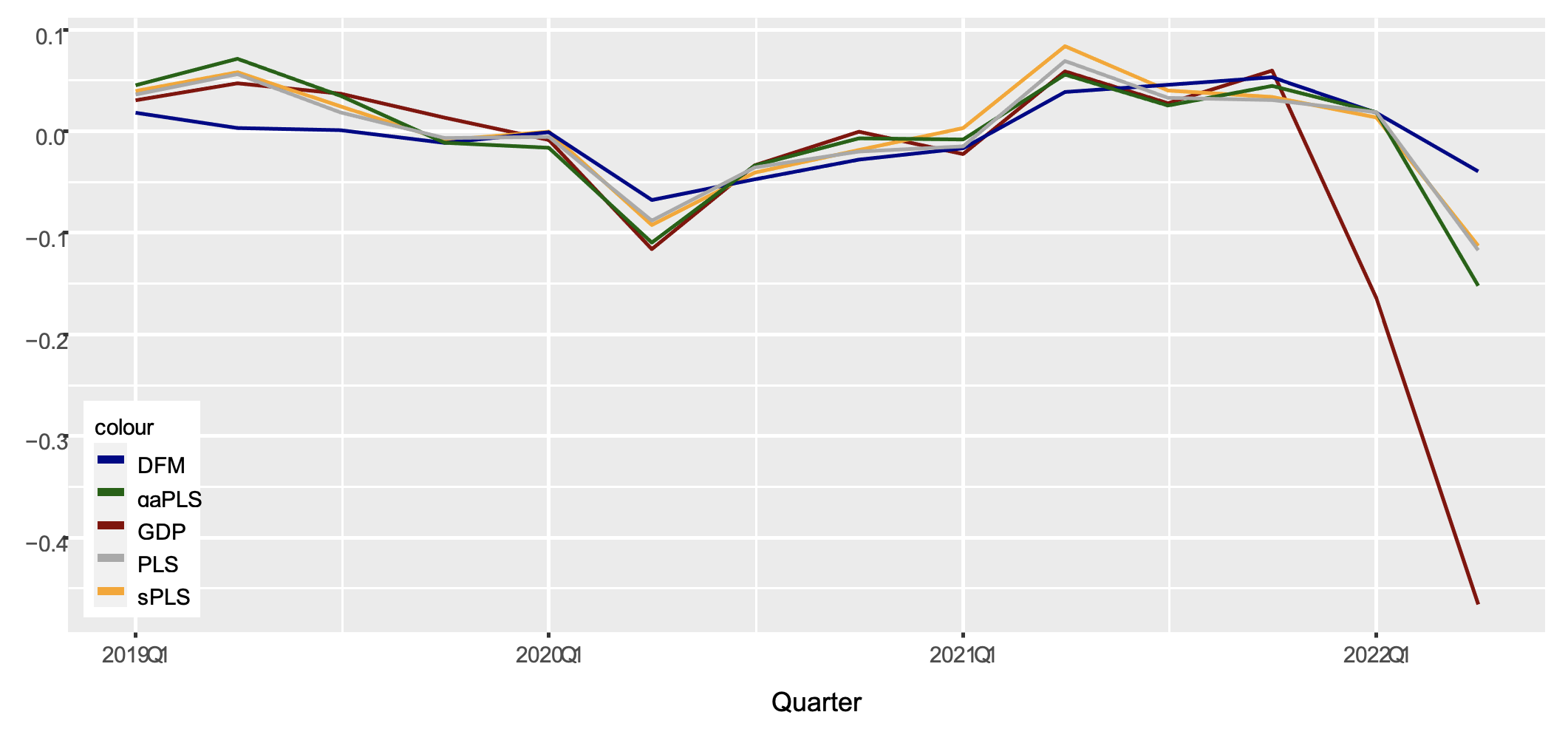
In Figure 1, the in-sample fit and out-of-sample nowcasts estimated using observed 2022 Google Trends are depicted for the dynamic factor model (DFM), the partial least squares factor model using the genetic algorithm as a feature selection method (gaPLS), the sparse partial least squares factor model a la Chun and Keleş (2010) (sPLS), and the regular partial least squares factor model without any pre-selection (PLS).
Figure 1 In-sample fit and out-of-sample nowcasts
The in-sample fit is much closer for partial least squares and its variants, as compared to dynamic factor model estimates. This should not be surprising as the partial least squares algorithm specifically targets the outcome variable, unlike principal component regressions.
The models trained on 2013 to 2021 data are employed to produce nowcasts for 2022Q1 and 2022Q2. The 2022Q2 value may be more properly considered a short-term forecast rather than a nowcast as in May 2022 Google Trends data were available, yet no other macro-data had been released since the start of the invasion.
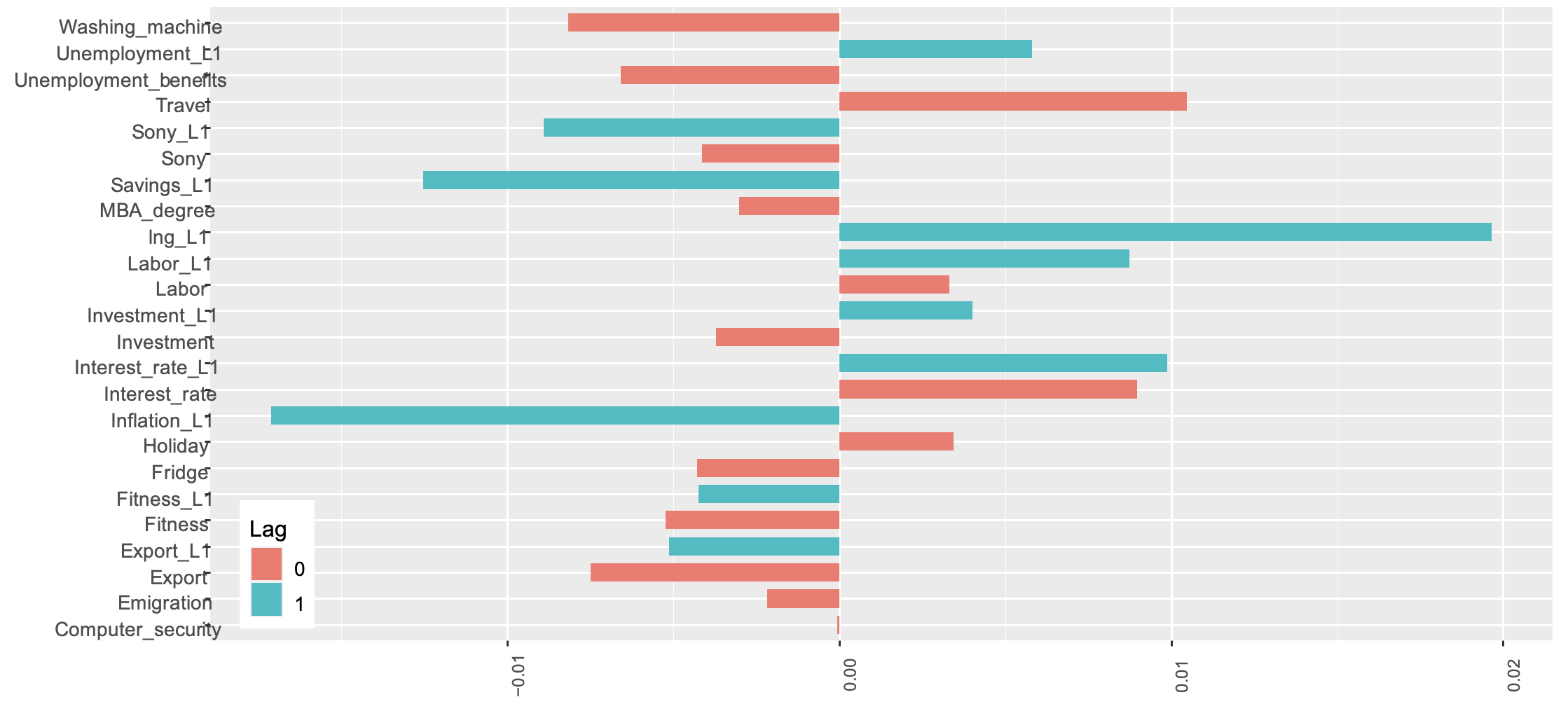
Which variables are selected and what are their regression parameters? In Figure 2 one may find the result of the genetic algorithm wrapper. All estimations are performed with standardised data. Note the high positive parameter associated with “lng L1”, the first lag of changes in GDP. The auto-regressive AR(1) component is autonomously picked by the algorithm, as it is part of the general pool of genes. A positive impact comes from contemporaneous changes in searches on ‘holiday’, ‘travel’, and ‘interest rate’, and lags in ‘unemployment’, ‘labour’, and ‘interest rate’. High past ‘inflation’ searches have a strong and negative impact on current GDP, as do changes in ‘savings’ and ‘Sony’.
Figure 2 Variable selection and parameter values
A regional partial least squares factor model used in policy applications produces accurate and robust aggregate nowcasts when regional cash turnover time series are used as inputs. This points towards the benefit of using high signal-to-noise data in conjunction with the developed routine.
Why are partial least squares latent factors different compared to principal component regressions? By explicitly targeting the outcome variable, partial least squares is better positioned to capture the correlation of features with the variable of interest by uncovering the few latent factors driving both target and input variables. Furthermore, partial least squares factors are not constrained to load on current and past values of variables in a uniform auto-regressive fashion. In a standard dynamic factor model, the auto-regressive parameters of the state space equation impose a structure on the relationship between factor representations that may not be faithfully present in the joint probability distribution of nowcasting variables.
Imposing sparsity guarantees irrelevant variables are excluded from the estimation stage altogether.
Conclusion
The proposed model building routine, factor estimation via partial least squares in conjunction with variable selection, uncovers in real-time the rapid, unprecedented contraction in Ukrainian GDP at the onset of the full-scale Russian invasion.
The continued widespread infrastructure destruction, from bombing of electricity production and distribution networks in 2022 to more recently agriculture production and shipping facilities, prevents the resumption of economic life and rebuilding of what has been damaged. The loss of human capital poses significant challenges in the reconstruction process.
When official statistical data are no longer available, the considered methodology offers a potentially improved nowcasting and near-term forecasting alternative to traditional dynamic factor models. The procedure is developed to account for the possible presence of irrelevant correlates among the input variables, as happens to be the case with non-standard data such as Google Trends.
Authors’ note: The views expressed in this column are those of the author and do not necessarily represent the views of the National Bank of Ukraine. The author would like to thank Ugo Panizza, Cédric Tille, and participants of the BCC 10th Annual Conference for their helpful comments and suggestions.
References
Chun, H and S Keleş (2010), “Sparse partial least squares regression for simultaneous dimension reduction and variable selection”, Journal of the Royal Statistical Society Series B: Statistical Methodology 72(1): 3–25.
Constantinescu, M, K Kappner and N Szumilo (2022), “Estimating the short-term impact of war on economic activity in Ukraine”, VoxEU.org, 21 June.
Constantinescu, M, K Kappner and N Szumilo (2023a), “The warcast index: Nowcasting economic activity without official data”, SSRN Working Paper.
Constantinescu, M (2023b), “Sparse Warcasting”, SSRN Working Paper.
Giannone, D, L Reichlin and D Small (2008), “Nowcasting: The real-time informational content of macroeconomic data”, Journal of Monetary Economics 55(4): 665–676.
Helland, I S (1990), “Partial least squares regression and statistical models”, Scandinavian Journal of Statistics 17(2): 97–114.
Stock, J H and M W Watson (2002), “Forecasting using principal components from a large number of predictors”, Journal of the American Statistical Association 97(460): 1167–1179.
Stock, J H and M W Watson (2012), “Dynamic factor models”, In M J Clements and D F Hendry, Oxford Handbook on Economic Forecasting, 35–60, Oxford: Oxford University Press.
Stoica, P and T Söderström (1998), “Partial least squares: A first-order analysis”, Scandinavian Journal of Statistics 25(1): 17–24.
Tsamardinos, I and C F Aliferis (2003), “Towards principled feature selection: Relevancy, filters and wrappers”, Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics, in Proceedings of Machine Learning Research, R4, 300-307.
Wold, S, H Martens and H Wold (2006), “The multivariate calibration problem in chemistry solved by the PLS method”, in B Kågström and A Ruhe (eds), Matrix Pencils. Lecture Notes in Mathematics 973: 286-293, Berlin, Heidelberg: Springer.
Wold, S, A Ruhe, H Wold and W J Dunn (1984), “The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses”, SIAM Journal on Scientific and Statistical Computing 5(3): 735–743.