Initial margin requirements for a portfolio of derivatives are typically calculated using a risk model, such as one of the well-known family of value-at-risk models. Most common risk models are procyclical. Margin requirements for the same portfolio are higher in times of market stress and lower in calm conditions. This can be an undesirable property, as a rise in margin requirements during a period of market stress could cause market participants to face funding strains.
Regulation has recognised that, subject to being adequately risk sensitive, margin models should not be ‘overly’ procyclical, both for margin models for centrally cleared (CPSS-IOSCO 2012) and non-centrally cleared (BCBS-IOSCO 2013) derivatives. There is, however, no standard definition of procyclicality. Our recent work proposes quantitative measures of procyclicality, and studies various margin models with regard to both their risk sensitivity and procyclicality (Murphy, Vasios, and Vause 2014).
Based on this analysis, we recommend that central counterparties and major dealers should disclose the procyclicality properties of their margin models, for example, by reporting the measures proposed in this column. This would help derivatives users to anticipate potential margin calls and ensure they have adequate holdings of, or access to, sufficient liquid assets.
Policy context
Regulators have long recognised that there is a potential issue for financial stability with margin models that are too procyclical. For instance, the Commodity Futures Trading Commission (CFTC 2013) highlights how big margin calls in a stressed market which cannot be met from liquidity at hand can either cause asset sales or defaults – both of which are destabilising.
The relevant European Regulation here contemplates a trade-off between risk sensitivity and procyclicality (European Union 2012). It requires that, “central counterparties (CCPs), competent authorities, and the European Securities and Markets Authority should, therefore, adopt measures to prevent and control possible procyclical effects in risk-management practices adopted by the CCPs, to the extent that a CCP’s soundness and financial security is not negatively affected.”
These policy considerations are supported by empirical and theoretical evidence. For instance, Brunnermeier and Pedersen (2009) model an economy in which investors face funding liquidity risk due to the possibility of future margin calls or losses on existing positions. They show that in this economy, there is a link between funding liquidity and market liquidity, and that this interaction can, under certain conditions, destabilise the market through a liquidity spiral.
Measures of procyclicality
In order to address the concerns about procyclicality, we need some measures of various aspects of the procyclicality of margin. We propose two types of quantitative measure of procyclicality:
- One that examines long-term margin variation; and
- One that focuses on short-term margin increases.
We start with the peak-to-trough measure. This is defined as the ratio of the maximum initial margin required for a constant portfolio to the minimum margin required over a fixed observation period. If the observation period is long enough to cover different phases of the business cycle, then this measure captures the variation of the margin across the cycle. In other words, this measure gives an estimate of long-term procyclicality.
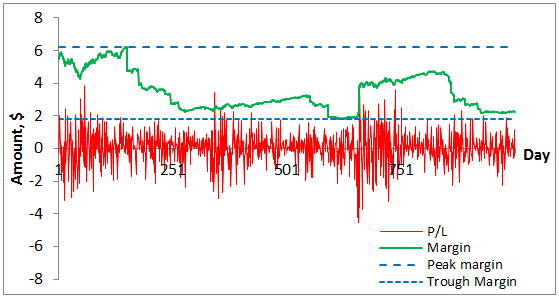
Figure 1 illustrates the peak-to-trough measure. Here, the red series is the daily log returns of a position in the S&P 500 total return index over a four-year period from 2009 to 2012, with an initial value of $100, and the upper green line is the margin required for that position calculated by a popular initial margin model (specifically, a historical simulation value-at-risk model). The margin required over the illustrated period varies from a peak of about $6.2 to a trough of about $1.8. Hence, the peak-to-trough ratio equals 3.44. The larger is this ratio, the more procyclical across the cycle is the margin model.
Figure 1. A financial asset return series and estimated margin for a position in that asset
We next move to the n-day procyclicality measure. This examines changes in margin over a shorter horizon. It is defined as the largest increase in margin over an n-day period for a constant portfolio over a fixed observation period. This measure captures the amount of extra margin that market participants would need to fund on a short-term basis, and hence it measures an important aspect of the liquidity risk of collateral assets.
Figure 2 zooms in on the period around day 658 of Figure 1 to illustrate the second measure of procyclicality. Here, the green line (right-hand scale) is the margin required, and the dotted orange line (left-hand scale) is the price of the underlying asset. The asset has heightened volatility from day 655 or so, causing the margin requirement to increase. For instance, the margin goes from $2.2 on day 658 to $3.75 the following day. This is the largest one-day increase in the data window; the blue dashed lines in the chart illustrate ‘before’ and ‘after’ margin levels. Five and thirty-day procyclicality measures can be calculated in a similar fashion.
Figure 2. Asset prices and margin requirements for a period generating a large one-day margin call
The performance of margin models
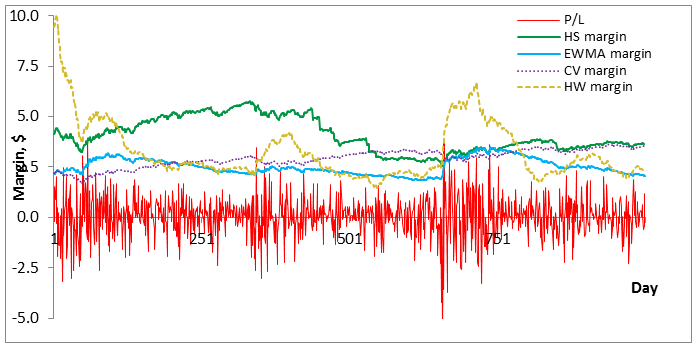
Figure 3 shows the initial margin estimates for a historical returns series from the S&P 500 total return index beginning in January 2009, as calculated by four popular margin models:
- Constant volatility (CV);
- Exponentially weighted moving average (EWMA) volatility;
- Historical simulation (HS) value-at-risk; and
- The Hull & White (HW) model.
We observe that although all models seem to be sensitive to changes in volatility, some models are more reactive than others. To elaborate upon this finding, we calculate risk sensitivity and the proposed procyclicality measures for each of the models.
Figure 3. Sample initial margin estimates from four margin models based on historical returns
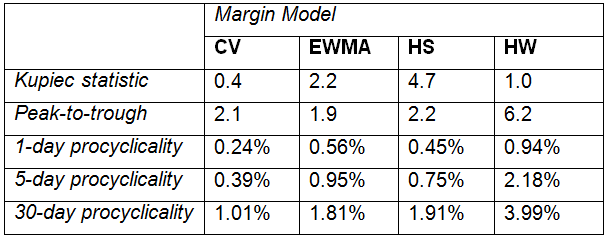
As a measure of risk sensitivity we use the Kupiec statistic, which measures whether the number of back test exceptions a margin model demonstrates is plausible, given the confidence level it purports to respect. A model with a Kupiec statistic below 6.6 is considered to be adequately risk sensitive. The results presented in Table 1 show that all four models react adequately to changes in risk.
Table 1. Risk sensitivity and procyclicality statistics for the models using historical returns
We next move to the procyclicality properties of margin models. The results in Table 1 illustrate some differences between the models. The simplest model – constant volatility – only demands a little over twice as much margin at the peak as at the trough, whereas the more reactive Hull&White model has roughly three times this range, i.e. six times as much margin at the peak as at the trough. The results of the n-day measures (here scaled by the asset value at the beginning of the n-day window) depict a similar picture. We see that the risk sensitivity of the more reactive model comes at the price of significantly bigger liquidity risk for margin posters. By any procyclicality measure, the Hull&White seems to be the most procyclical of the initial margin models studied.
More generally, the variation in the procyclicality may come not only from different models (as presented in this article), but also from different parameter settings in a given model, or different strategies for updating parameter values in the light of new data.
Conclusions
Our analysis has shown that initial margin models which pass common risk sensitivity tests can have very different levels of procyclicality. How should authorities and market participants respond?
First, they could compute procyclicality measures to better understand, assess, and compare the procyclicality of existing and potential future initial-margin models. In this article, we suggested two such measures which may be useful.
Second, central counterparties and large dealers could disclose both peak-to-trough and n-day procyclicality measures for their margin models. This would help clearing members and their clients to anticipate potential increases in margin requirements, and to prepare accordingly.
Finally, armed with measures of procyclicality, international authorities would be better able to investigate the extent to which it can be reduced, without breaching risk-sensitivity requirements, through policies such as stressed calibration, margin floors, and speed limits on margin calls. We plan to investigate this issue in future work.
References
Basel Committee on Banking Supervision and International Organization of Securities Commissions (2013), “Margin requirements for non-centrally cleared derivatives”, September.
Brunnermeier, M and L Pedersen (2009), “Market liquidity and funding liquidity”, Review of Financial Studies, Vol. 22. No. 6, pages 2,201–38.
Committee on Payment and Settlement Systems and Technical Committee of the International Organization of Securities Commissions (2012), “Principles for financial markets infrastructures”, April.
Commodity Futures Trading Commission (2013), “Enhanced risk management standards for systemically important derivatives clearing organizations”, Final Rule 17 CFR Part 39, August.
European Union (2012), “Regulation (EU) No. 648/2012 on OTC derivatives, central counterparties and trade repositories”, July.
Murphy D, M Vasios, and N Vause (2014), “An investigation into the procyclicality of risk-based initial margin models”, Bank of England Financial Stability Paper No. 29, May.